Kochi University
Faculty of Agriculture and Marine Sciences / IoP Collaborative Creation Center
Laboratory of Environmental Control
for Crop Production
高知大学 農林海洋科学部 / IoP共創センター
作物環境調節学研究室
球面三角形の余弦定理
球面三角形の余弦定理
参考: MY MATH NOTEの記事を参考にしました。
図のような球面三角形ABCの辺a,b,c と
角Aとの間には、以下の関係が成り立つ(球面三角形の余弦定理)
\[\qquad \cos a=\cos b \cdot \cos c +\sin b \cdot \sin c \cdot \cos A \qquad \text{\textemdash} \: (1) \]
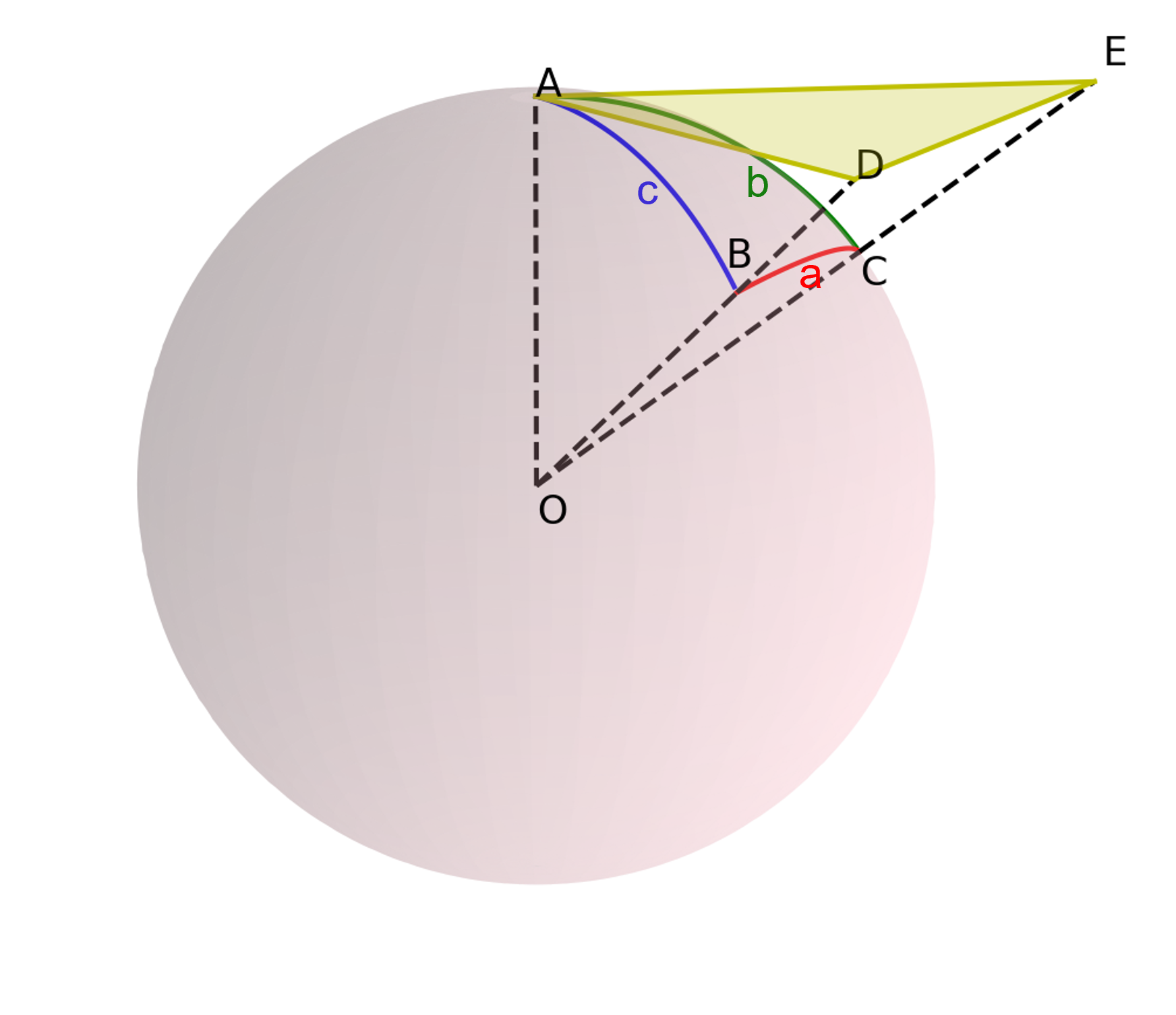
よって、 \( \text{OA} \perp\ \text{平面ADE} \) より、 \( \text{OA} \perp \text{AD},\quad \text{OA} \perp \text{AE} \)である。 したがって \(\triangle \text{ODA}\) と \(\triangle \text{OEA}\) は直角三角形となる。
また、\(\angle \text{DOE}=\angle \text{BOC}=a,\quad \angle \text{DOA} =\angle \text{BOA}=c \) である。
\(\triangle \text{ODE} \) と \( \triangle \text{ADE} \) に平面三角形の余弦定理を用いて
\[\ DE^2=OD^2+OE^2-2OD\cdot OE\cos a\] \[\ DE^2=AD^2+AE^2-2AD\cdot AE\cos A\]
辺々引いて
\[(OD^2-AD^2)+(OE^2-AE^2)-2OD\cdot OE\cos a+2AD\cdot AE\cos A=0\]
\[ 2OD\cdot OE\cos a = (OD^2-AD^2)+(OE^2-AE^2)+2AD\cdot AE\cos A\\ = OA^2+OA^2+2AD\cdot AE\cos A\\ = 2OA^2+2AD\cdot AE\cos A\\ \] ※上記では、三平方の定理を\(\text{OD}^2\)および\(\text{OE}^2\)にそれぞれ適用した。
\[\therefore OD\cdot OE\cos a=OA^2+AD\cdot AE\cos A\]
これを整理すると、
\[ \cos a = \frac{OA^2}{OD\cdot OE}+\frac{AD\cdot AE}{OD\cdot OE}\cos A\\ = \frac{OA}{OE}\cdot \frac{OA}{OD}+\frac{AE}{OE}\cdot \frac{AD}{OD}\cos A\\ \\ = \cos b \cdot \cos c +\sin b \cdot \sin c \cdot \cos A\\ \]
となり、式(1)が導ける。
光線と葉の法線とのなす角がつくる余弦
前節の球面三角形の余弦定理 (式(1))は、
光線方向への葉面積の投影関数(いわゆるG関数)を求める際に必要となる。
ここでは、その概略を示す。
下図は、半径1の球を示している(よって、弧の長さ = 角度)。
A, Bの天頂角をそれぞれ\( \theta,\theta_L \) とし、
A, Bの方位角の差を\( \alpha - \alpha_L \) とする。
図中のNは天頂である。
球面三角形NABに余弦定理を用いると、\( \cos{\widehat{r_L r}} \)は、
\[ \cos{\widehat{r_L r}} = \cos \theta \cos \theta_L + \sin \theta \sin \theta_L \cos{(\alpha - \alpha_L)}\]
と表せる。
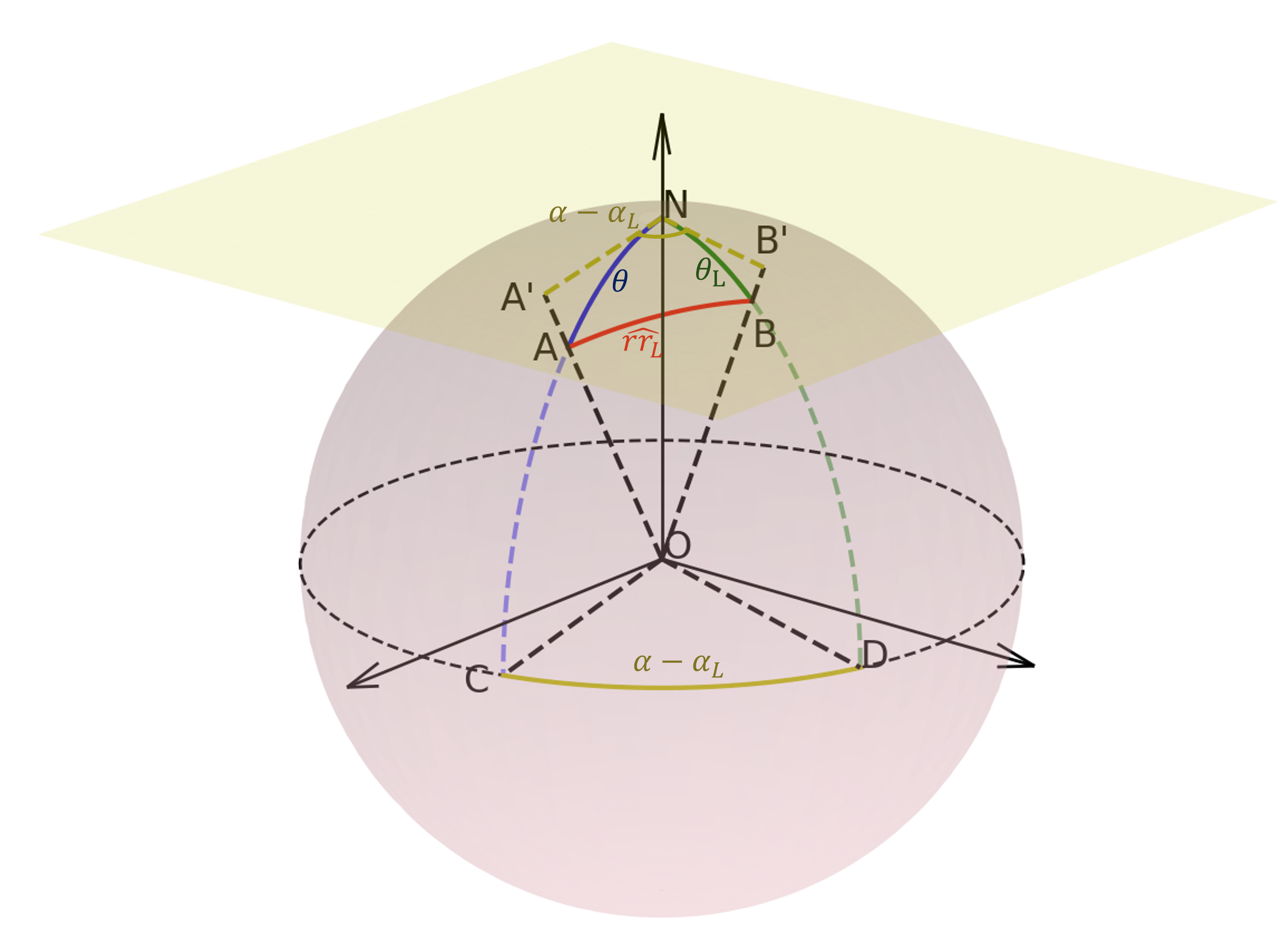
\( \cos{\widehat{r_L r}} \)は、葉角の確率密度関数から、 光線方向への投影関数(いわゆるG関数)を求める際に使用する。 光線をベクトルAO、葉の法線をOBとすれば、\( \cos{\widehat{r_L r}} \)は、 光線方向への、葉面積の投影率を表している。