Laboratory of Environmental Control
for Crop Production

光線の透過率（gap fraction）

ここでは、葉群が空間的にランダムに分布している場合について述べる （Nomura et al. (2020)で説明している）。 より一般的な場合については、Nilson (1971)を参照のこと。

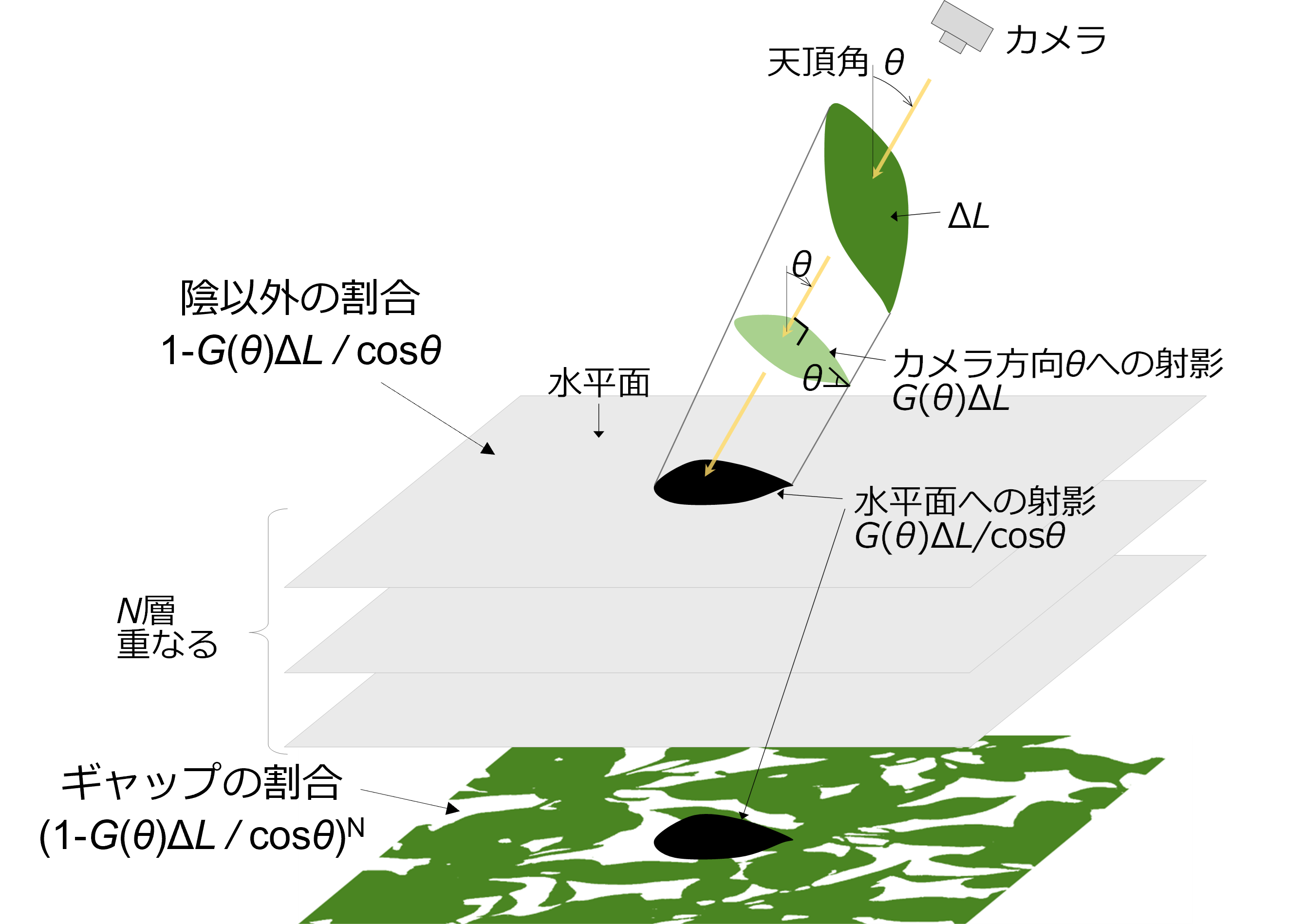
葉面積指数\( L \) \( ( \text{m}^2 \; \text{m}^{-2} )\) の葉群を\( N \)層に分ける。 \( N \)は大きな値とする。 それぞれの層は、微小葉面積指数\( \Delta L_i \) \( ( \text{m}^2 \; \text{m}^{-2} )\) (\(i = 1,2,・・・N \))を持っているとする。 それぞれの層の厚さは、\( \Delta L_i \)がすべて同じ値に なるように選ぶことができる（\( \Delta L_i = \Delta L \)） 。 これらの\( \Delta L \)が、水平面に投影する面積は、 \[ \Delta L_{hor} = \frac{G(\theta) \Delta L_i}{\cos\theta} \] である。 ここで、\( \theta \)は観測者あるいは太陽の天頂角、 \( G(\theta) \)は、\( \theta \)方向への葉の投影率である。 上式は、 「微小葉面積指数\( \Delta L \)によって水平面に投影される影の面積は、 \( \Delta L_{hor} \)である」ことを示している（単位土地面積あたり）。 影になっていない面積は、単位土地面積あたりでは\(1 - \Delta L_{hor} \)である。
\( N \)層ある場合、水平面のある点が、影に隠れていない確率（\( P_0 \)）は、 葉が空間的にランダムに位置しているとすれば、 \[ P_0 = (1 - \Delta L_{hor})^N = (1- \frac{G(\theta) \Delta L}{\cos\theta} )^N \] となるはずである。ここで、定義より、\( \Delta L = L / N \) であるので、 これを代入して、\( N \rightarrow \infty \)を取ると、 ネイピア数e (= 2.718...)の定義 を参考に、 \[ P_0 = \exp{ \left( - \frac{G(\theta)}{\cos\theta} L \right) } \] となる（ちなみに\( \exp{(x)} \)はeのx乗を表す）。上式は、「直達光が葉群に遮られずに、ある深さ\( L \)まで到達する確率」、 あるいは、「葉群の上\( (L = 0) \)の直達光強度を1としたときの、ある深さ\( L \)における直達光強度の平均値」とみなすことができる （ただし、葉に当たった光はすべて吸収される（= 葉は黒体）と仮定したとき）。 また、カメラ画像から\( L \)を推定する際、「カメラ画像に含まれるギャップ（背景）の割合」とみなすこともできる。 カメラ画像に含まれるギャップ（背景）の割合\( P_0 \)は、画像解析によって求められるので、 前式を\( L \)について解けば、 \[ L = - \frac{\cos\theta}{G(\theta)} \ln{P_0} \] となり、\( L \)を推定できる （ただし、\( G(\theta) \)があらかじめわかっている必要がある）。 なお、\( \ln{x} \)は、\( x \)の自然対数（= 底をネイピア数eとした対数）である。