Kochi University
Faculty of Agriculture and Marine Sciences / IoP Collaborative Creation Center
Laboratory of Environmental Control
for Crop Production
高知大学 農林海洋科学部 / IoP共創センター
作物環境調節学研究室
葉の角度分布とG関数
葉の角度分布とは
葉の角度分布(leaf angle distribution)とは
「葉群のうち、\( \theta \)°だけ傾いた葉は何パーセント存在するか」を示したものである。
見過ごされがち(?)だが、葉角は、作物の光合成、蒸散、葉温などに、重大な影響を及ぼす。
例えば、水平な葉が多い葉群では、真上から射し込んだ光は上層で多くインターセプトされ、下層には届きにくくなる。
水平葉が多い葉群は光を地面に逃しづらいので、作物の葉面積指数が小さい間(例:定植直後)は光合成に有利かもしれない。
一方、葉面積指数が増えすぎた状況下では、下層の葉には光が行き届きにくくなるので、
葉群全体の光合成速度は低下するかもしれない。
また、Lambertの余弦則
(光線と葉とのなす角によっても、単位葉面積あたり、単位時間あたりに葉が受ける光量子数(= 光量子束密度)が変わること)
を考えても、葉角は、作物の生理・生態を語るうえで、
大変重要な因子であるといえる。
葉の角度の確率密度関数(Ross, 1981)
予備知識;立体角
高校数学で習ったように、平面上では、円の中心角を「半径が1の円における円弧の長さ(ラジアン)」で表現する。
同様に、三次元でも、球の中心から広がる円錐の立体的な角度(のようなもの)を、
「半径が1の球を切り取ってできる円錐の底面積」で表現することが可能である。
これを、立体角という(単位はsteradian;ステラジアン)。
予備知識;確率密度
ある変数\( x \)が\( a \)以上\( b \)以下の値をとる確率が
\[ \int_{a}^{b} f(x) dx \]
で与えられるとき、\( f(x) \)を、確率密度関数という。
ある変数が、ある特定の値をとる確率を考える。
値が連続的に変化するような変数の場合、「ぴったりの値」になる確率は限りなく低い
(というか数学的には0になる)。
例えば、寿命が30日~50日の昆虫が、ぴったり31日2時間20分11.3000...秒に
死んでしまう確率は限りなくゼロに近い。
一方、そのような昆虫が、ある幅のある時間(例えば31日~35日の間)に死んでしまう確率であれば、
まとまった大きな確率になりそうである。
この例では、「特定の時間範囲内に昆虫が死亡する確率」を「その時間範囲の長さ」で割った値を
「確率密度」と定義する。この場合、確率密度は「単位時間あたりの確率」として定義される。
言い換えれば、「確率密度」を「時間」で積分することで「確率」となる。
次節以降で葉の角度分布を考える場合、「特定の角度範囲内に、葉の角度が含まれる確率」を「その角度範囲」で割った値を、
「葉角の確率密度」と定義できる。「葉角の確率密度」の関数を「角度範囲」で積分することで
「確率」となる。
言い換えれば、「葉角の確率密度」を「角度範囲」で積分することで、「特定の角度範囲内に、葉の角度が含まれる確率」を計算できる。
葉角の確率密度関数
ある点\( P \)の回りの、ある体積\( V^*(P) \)に存在する葉群について考える。
この体積の中に存在する葉の角度の分布を知りたい。
葉群の葉の角度(向き)は、葉の法線ベクトル (leaf normals; 葉に垂直なベクトル)として
特徴づけられる。通常葉は上を向いているので、あらゆる葉は、
球の上半分(上半球)のいずれかの方向を向いている、と考えることができる。
今、上半球を、それぞれが微小な立体角\( \Delta \Omega_L = \sin \theta_L \Delta \theta_L \Delta \alpha_L \)
をもつ小面積に分割する(下図参照)。なお、図に示す通り、\( \alpha_L \)は葉の向きの方位角、\( \theta_L \)は傾斜角である。
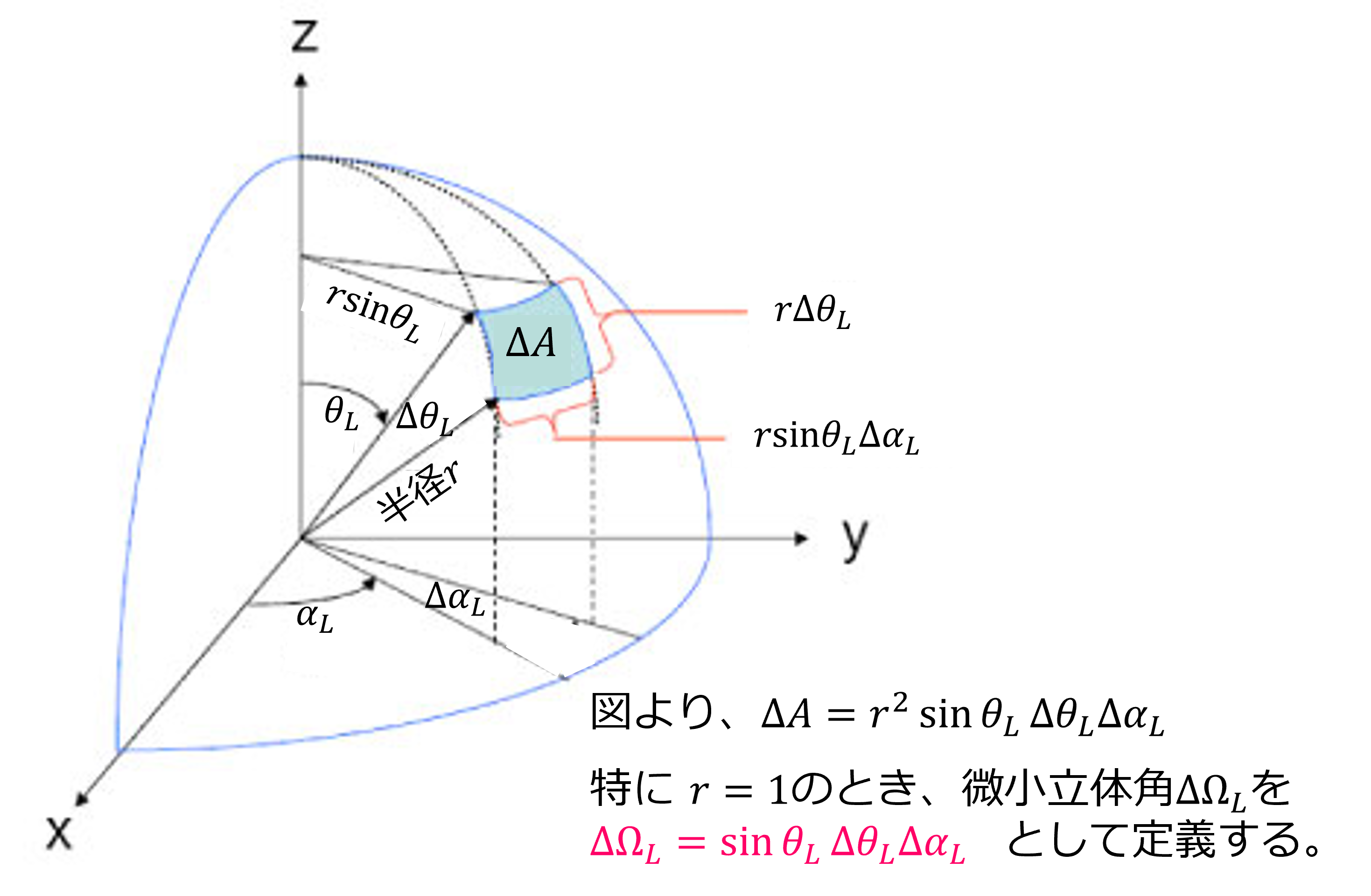
\( i \)番目の立体角を\( \Delta \Omega_{Li}\)とし、この立体角の法線ベクトルを\( r_{Li} \)とする。 この立体角に属する葉(= 法線ベクトルが大体\( r_{Li} \)の葉)の面積の合計を\( \Delta S^*_{Li}\)とする。 葉群のすべての葉の面積の合計を\( \Sigma_{i} S^*_{Li}\)とすれば、この立体角に属する葉の割合は、 \( \frac{\Delta S^*_{Li}}{\Sigma_{i} S^*_{Li}} \)である。 この割合を、すべての\( i \)で足し上げれば、1になる。
ここで、ある葉が\( \Delta \Omega_{Li}\)という立体角に属する確率密度関数\( f(P, r_{Li}) \)(= 立体角あたりの確率)を考える。 この確率密度\( f(P, r_{Li}) \)に、そのときの微小立体角\( \Delta \Omega_{Li}\)をかけたものは、 \( \frac{\Delta S^*_{Li}}{\Sigma_{i} S^*_{Li}} \)と一致する。数式で書けば、 \[ f(P, r_{Li}) \Delta \Omega_{L}\ = \frac{\Delta S^*_{Li}}{\Sigma_{i} S^*_{Li}} \] である。上記の数式を、立体角が取り得る範囲全体(= 上半球; \( \Omega_1 \)と表記する )で積分すると、確率の定義から、1にならなければならない。 すなわち、 \[ \int_{\Omega_1} f(P, r_{L}) d\Omega_{L}\ = 1 \qquad \text{\textemdash} \: (1)\] である。 ここで、すべての葉角が一様な確率で発生する場合を考える(すなわち、\( f(P, r_{L}) = 定数\) のとき)。 この定数には、どのような値が入るだろうか?これを考えるためには、 式(1)に\( \Delta \Omega_L = \sin \theta_L \Delta \theta_L \Delta \alpha_L \)を式(1)に代入して、 \[ \int_{0}^{2\pi} \int_{0}^{\pi/2} 定数 \; \sin \theta_L d \theta_L d \alpha_L = 1\] となるように定数を決めればよい。上式を「定数」について解くと(ふつうに二重積分を計算する。定数は積分の外に出せる。)、 \[ 定数 = \frac{1}{2\pi} \] となる。そこで、一歩踏み込んで、葉角の確率密度関数\( f(P, r_{L}) \)を \[ f(P, r_{L}) = \frac{1}{2\pi} g_L(P, r_L) \qquad \text{\textemdash} \: (2)\] と書くことにする。つまり、\( \frac{1}{2\pi} g_L(P, r_L) \)が、葉角の確率密度関数であり、 \( g_L(P, r_L) \)の値は、葉群の性質によって決定づけられる。 例えば、すべての葉角が一様な確率で発生する場合、\( g_L(P, r_L) = 1\)である。
式(1)に式(2)を代入すると、 \[ \frac{1}{2\pi} \int_{\Omega_1} g_L(P, r_{L}) d\Omega_{L}\ = 1 \qquad \text{\textemdash} \: (3)\] となる。式(3)に\( \Delta \Omega_L = \sin \theta_L \Delta \theta_L \Delta \alpha_L \)を代入して整理すると、 \[ \int_{0}^{2\pi} \int_{0}^{\pi/2} \frac{1}{2\pi} g_L(P, \alpha_L, \theta_L) \; \sin \theta_L d \theta_L d \alpha_L = 1 \qquad \text{\textemdash} \: (4)\] となる。ここで、多くの研究では、葉の方位角\( \alpha_L \)の確率密度は一様分布だと仮定される(必ずしもそうではないが)。 つまり、\( g_L(P, \alpha_L, \theta_L) \)は、方位角には依存しないものと仮定されることが多い。 この場合、 \[ \hat{g} (P, \theta_L) = \frac{\sin \theta_L}{2\pi} \int_{0}^{2\pi} g_L(P, \alpha_L, \theta_L) d \alpha_L \qquad \text{\textemdash} \: (5)\] という関数を定義すれば、式(4)は、 \[ \int_{0}^{\pi/2} \hat{g} (P, \theta_L) d \theta_L = 1 \qquad \text{\textemdash} \: (6)\] と書くことができる。ここで、\( \hat{g} (P, \theta_L) \)は、 ある葉が傾斜角\( \theta_{L}\)をとる確率密度関数(= 傾斜角\( \theta_{L}\)あたりの確率。傾斜角\( \theta_{L}\)で積分すれば確率になる)である。 この表現も、しばしば既往文献に登場する。
G関数
葉群内の光(放射)の透過をモデリングする場合や、
画像から葉面積指数を推定する場合などには、
葉角の確率密度関数\( \frac{1}{2\pi} g_L(P, r_L) \)ではなく、
以下で定義されるG関数(G-function)という関数が頻繁に登場する (式(7));
\[ G(P,r) = \int_{\Omega_1}^{} \frac{g_L(P, r_{L})}{2\pi} |\cos{\widehat{r_L r}}| d\Omega_{L}\ \qquad \text{\textemdash} \: (7)\]
ここで、\( \widehat{r_L r} \)は、葉の向き(法線ベクトル)と光線方向とのなす角である。
図形的には、以下のように解釈できる。
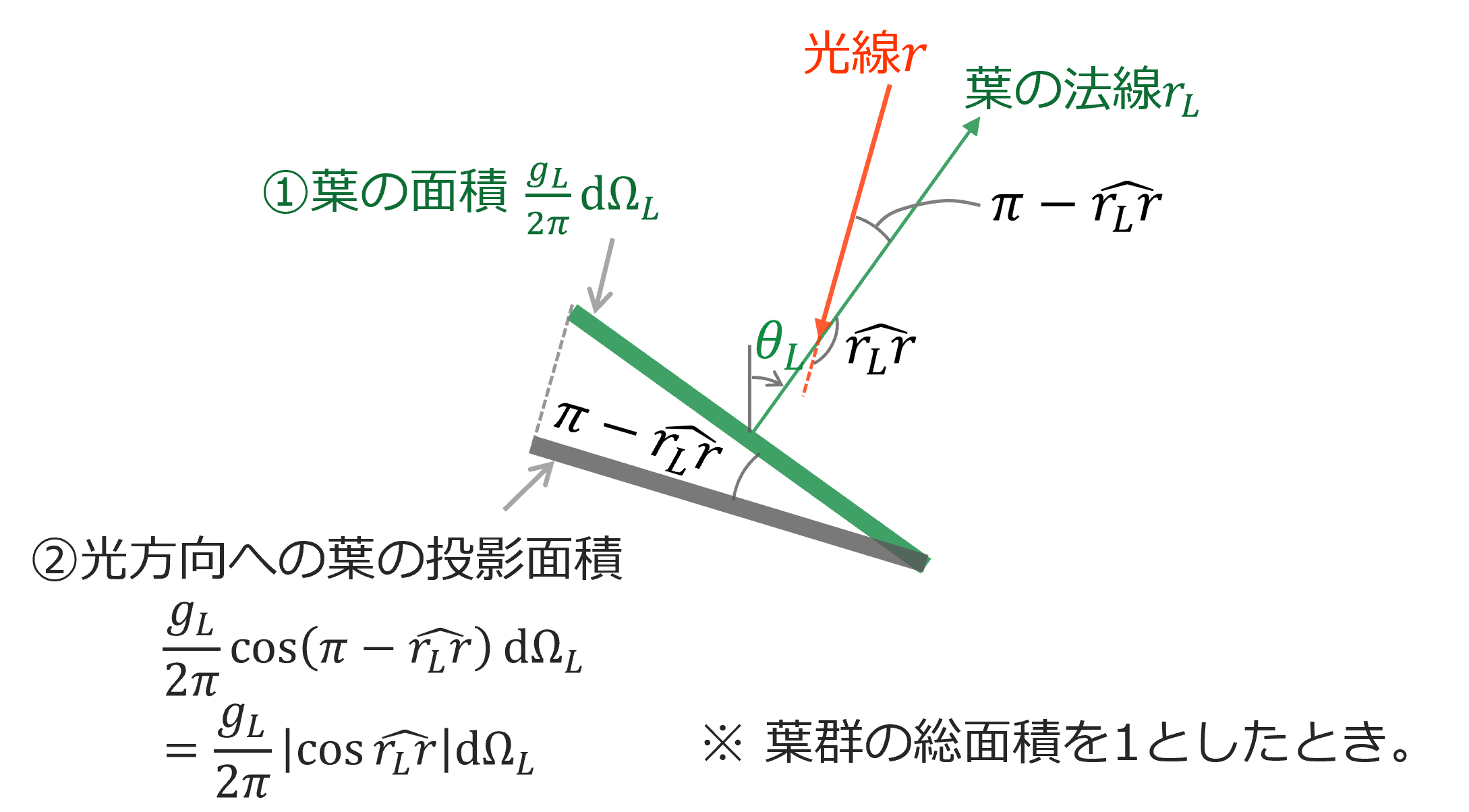
なお、\( \cos{\widehat{r_L r}} \)は、球面三角形の余弦定理によって、以下の数式で表される。 \[ \cos{\widehat{r_L r}} = \cos \theta \cos \theta_L + \sin \theta \sin \theta_L \cos{(\alpha - \alpha_L)} \qquad \text{\textemdash} \: (8)\] ここで、下付きの\( _L \)がついていない角度は、光線の角度であり、\( \theta \)は光線の傾斜角(天頂角)、\( \alpha \)は光線の方位角である。 式(8)の詳細は球面三角形の余弦定理を参照のこと。
式(7)に、式(8)および \( \Delta \Omega_L = \sin \theta_L \Delta \theta_L \Delta \alpha_L \)を 代入して整理すると、 \[ G(P,r) = \int_{0}^{2\pi} \int_{0}^{\pi/2} \frac{g_L(P, \alpha_L, \theta_L)}{2\pi} |\cos \theta \cos \theta_L + \sin \theta \sin \theta_L \cos{(\alpha - \alpha_L)}| \sin \theta_L d \theta_L d \alpha_L \qquad \text{\textemdash} \: (9)\] となる。