最終更新日 2007年6月9日
TinyBasic の使い方

TINY BASIC Ver.1.1
の使い方
上のテキストエリアに次のような BASIC のプログラムを入力して、
100 LET A=0
110 LET B=2
120 INPUT N
130 FOR I=1 TO N
140 LET C=(A+B)/2
150 LET D=C*C*C-5
160 IF D<0 THEN LET A=C
170 IF D>=0 THEN LET B=C
180 NEXT I
190 PRINT A
200 PRINT B
210 END

RUN ボタンをクリックして、
下のテキストエリアのプロンプト ? に続けて、3を入力して、
改行すれば、次のように表示されます。

これは2007年のセンター試験の問題のプログラムで、二分法で5の立方根を求めるものです。この Tiny Basic は高等学校の数学の教科書にあるプログラムを実行するための
最小限度の機能を備えたものです。高等学校の数学の教科書の BASIC は
多分誰も教えていないと見えて、随分バラエティーがありましたが、
公約数というか、私が昔マイコン時代に使っていた Basic のサブセット
+αです。基本的には、数値計算と平面グラフィックスしかできません。
データ構造は、実数だけで、文字列は、非常に制限した形でしか使えません。
次のような問題を考えてみます。
例題:円の半径 r の値を入力し、周の長さと面積を求める BASIC の
プログラムを作れ。
解答例:次のようなプログラムを作ればいいです。
10 INPUT R
20 P=3.141592
30 C=2*P*R
40 S=P*R*R
50 PRINT C
60 PRINT S
70 END
上側のテキストエリアに上の BASIC のプログラムを入力して、

RUN ボタンをクリックすれば、
の様に、下側のテキストエリアに、プロンプトが表示されるので、
R に入力する数値を半角で打ち込みます。ENTER キーを押せば、
実行結果が下のテキストエリアに表示されます。
テキストエリアには、自動的にスクロールバーが現れます。
旺文社の数学 A の昔の教科書には、次のような最大公約数を求めるプログラムが載っています。
10 REM 最大公約数
20 INPUT "N, M "; N, M
30 G=N
40 IF N>INT(N/G)*G THEN 80
50 IF M>INT(M/G)*G THEN 80
60 PRINT "最大公約数=";G
70 GOTO 100
80 G=G-1
90 GOTO 40
100 END
私の Tiny Basic では、行番号は必要最小限度で良いです。
REM 最大公約数
INPUT "N, M "; N, M
G=N
40 IF N>INT(N/G)*G THEN 80
IF M>INT(M/G)*G THEN 80
PRINT "最大公約数=";G
GOTO 100
80 G=G-1
GOTO 40
100 END
このプログラムを実行すると

となります。
10 REM 最大公約数
は、コメント文で、コンピュータは無視します。REM があるとその行を無視します。
BASIC は大文字と小文字は区別しません。
10 rem 最大公約数
でも
10 Rem 最大公約数
でも良いです。
20 INPUT "N, M"; N, M
は、"N, M" と表示して、改行せずに(セミコロン ; があるので)、コンマで区切られた二つの数字の入力を待ち、入力されると、N と M に代入します。
30 G=N
は、代入文で G に N を代入しています。
30 LET G=N
が正式な書き方ですが、Tiny Basic では LET は省略できます。
40 IF N>INT(N/G)*G THEN 80
は、IF 文で、「N を G で割った余りが 0 でなければ、80 行に飛びなさい」という命令です。何故、こういう意味になるかというと、組み込み関数 INT() は小数部分を切り捨てなさいという関数なので、INT(N/G)*G は、N が G の倍数であれば、N になりますが、N が G で割り切れないときには N より小さくなるからです。同じく、
50 IF M>INT(M/G)*G THEN 80
は、「M を G で割った余りが 0 でなければ、80 行に飛びなさい」という命令です。
40 IF N>INT(N/G)*G THEN 80
50 IF M>INT(M/G)*G THEN 80
は、
40 IF N>INT(N/G)*G THEN GOTO 80
50 IF M>INT(M/G)*G THEN GOTO 80
の省略形です。
昔の BASIC (私の BASIC も)の IF 文は1行にしか書けません。
書式の一つ目は
IF 論理式 THEN 「真のとき実行する文」
で、論理式が真であれば「真のとき実行する文」を実行します。もう一つの書式は
IF 論理式 THEN 「真のとき実行する文」 ELSE 「偽のとき実行する文」
で、論理式が真であれば「真のとき実行する文」を実行し、
論理式が偽であれば「偽のとき実行する文」を実行します。 文はコロン : で区切って、複数の文を書くことができます。IF 文はネストできません。
更に
40 IF N>INT(N/G)*G THEN 80
50 IF M>INT(M/G)*G THEN 80
は
40 IF N>INT(N/G)*G OR M>INT(M/G)*G THEN 80
と、一行で書くこともできます。論理演算子として、NOT, AND, OR が使えます。
否定、論理積、論理和です。基本論理式としては
算術式 = 算術式
算術式 <> 算術式
算術式 < 算術式
算術式 > 算術式
算術式 <= 算術式
算術式 >= 算術式
が使えます。上の端は等しいければ、二番目は等しくなければ真となります。
本当は、Java の様に厳しくはなく、任意の算術式が使え、0 が偽で、それ以外は
真です。
AND と OR は二項演算子として定義しているので
60 IF X>Y AND X>Z AND Y>Z THEN PRINT X,Y,Z
のような使い方は現在は、TinyBASIC では出来ません。
60 IF (X>Y AND X>Z) AND Y>Z THEN PRINT X,Y,Z
か
60 IF X>Y AND (X>Z AND Y>Z) THEN PRINT X,Y,Z
のように、括弧を付けて、二項演算子として使って下さい。OR も同様です。
60 PRINT "最大公約数=";G
で、最大公約数=という文字列と G の値を続けて表示し、改行します。
70 GOTO 100
は、「100 行に飛びなさい」(つまり、「次は100と数字がふられた命令を実行しなさい」)という命令です。
80 G=G-1
の代入文で、G を 1 減らします。
90 GOTO 40
は、「40 行に飛びなさい(戻りなさい)」という単純 GOTO 文です。
100 END
は、「停止しなさい」という命令です。
次は素因数分解の例です。サブルーチンと FOR NEXT 文を使った例です。
100 REM 素因数分解
110 INPUT "自然数N(5桁以内)を入力 N=";N
120 PRINT N
130 IF N<2 THEN END
140 IF N>INT(N/2)*2 THEN 180
150 PRINT "2.0";
160 N=N/2
170 GOTO 130
180 GOSUB 300
190 N=M
200 IF N>1 THEN 180
210 END
300 FOR I=3 TO SQR(N) STEP 2
310 IF N=INT(N/I)*I THEN 360
320 NEXT
330 PRINT N
340 I=N
350 GOTO 370
360 PRINT I;
370 M=N/I
380 RETURN
を実行し、12345 を入力すると、

と、アップレットはなり、
自然数N(5桁以内)を入力 N=12345
12345.0
3.0 5.0 823.0
と表示されます。
180 GOSUB 300
が、サブルーチンの呼び出しで、300 行に飛びます。GOTO 300 との違いは、
GOSUB 300 は RETURN に出会うと、GOSUB 300 のあった行の次の行に戻って、
今の場合は
190 N=M
を実行することです。
300 FOR I=3 TO SQR(N) STEP 2
310 IF N=INT(N/I)*I THEN 360
320 NEXT
330 PRINT N
340 I=N
350 GOTO 370
360 PRINT I;
370 M=N/I
380 RETURN
が、サブルーチンです。サブルーチンには、引数も局所変数もありません。
変数はすべてグローバル変数です。
300 FOR I=3 TO SQR(N) STEP 2
310 IF N=INT(N/I)*I THEN 360
320 NEXT
は、FOR NEXT 文です。
300 FOR I=3 TO SQR(N) STEP 2
・・・・・
320 NEXT
は、Java の
for (I=3; I<=Math.sqrt(N); I=I+2) {
・・・・・
}
と同じです。この FOR NEXT 文 を、IF 文と GOTO 文で作った
300 I=3
310 IF N=INT(N/I)*I THEN 360
315 I=I+2
320 IF I<=SQR(N) THEN 310
と比べて下さい。同じ意味ですが、IF 文と GOTO 文だけでプログラムを作った時より、 FOR NEXT 文 を使うと、プログラムの構造が浮き上がってきて、ずっとプログラムが読みやすくなります。
300 FOR I=3 TO SQR(N) STEP 2
・・・・・
320 NEXT
という文法の BASIC と
300 FOR I=3 TO SQR(N) STEP 2
・・・・・
320 NEXT I
と、NEXT の後ろに、制御変数の I を付ける文法の BASIC がありますが、
私の BASIC は、NEXT の後ろに、制御変数の I は付けても、付けなくてもいいです。
STEP が省略されると増分は1になります。STEP に負の数を指定することができます。このときは、STEP で指定した値を変数に加えながら(従って、変数は小さくなっていく)、変数が TO で指定した値以上である間はループを繰り返します。増分と終わりの値は最初に一度だけ評価されます。NEXT 文はネストできます。
従って、
300 FOR I=3 TO SQR(N) STEP 2
310 IF N=INT(N/I)*I THEN 360
320 NEXT
は、N の最小の約数を求めています。N より小さい約数が見つかれば、360 行へ飛びます。そのとき、最小の約数が I にセットされています。N が素数のときは、FOR NEXT 文の実行が終わります。従って、サブルーチン
300 FOR I=3 TO SQR(N) STEP 2
310 IF N=INT(N/I)*I THEN 360
320 NEXT
330 PRINT N
340 I=N
350 GOTO 370
360 PRINT I;
370 M=N/I
380 RETURN
は、N の最小の約数(従って、素数)を求め、それを表示し、それで N を割った値を M に代入しています。
次は、関数定義 DEF 文と WHILE WEND 文を使った例です。普通の昔の BASIC には
WHILE WEND 文はありませんが、組み込むのが簡単だったので組み込んでいます。
二次関数 f(x)=ax^2+bx+c の係数 a, b, c と範囲の下限 L と上限 M を入力し、
x を L から M まで 1 ずつ増加させたときの f(x) の値を求めて、x の値と f(x) の値を出力するプログラムです。
INPUT A, B, C, L, M
DEF FNF(X)=A*X*X+B*X+C
N=L
WHILE N<=M
PRINT N, FNF(N)
N=N+1
WEND
END
実行して、1,1,1,1,5 を入力すると
? 1,1,1,1,5
1.0 3.0
2.0 7.0
3.0 13.0
4.0 21.0
5.0 31.0
となります。
DEF FNF(X)=A*X*X+B*X+C
が、関数 FNF(X) の定義です。FNF(式) の形式で呼び出されたとき、
FNF(X)=A*X*X+B*X+C
の X を式の値にしたときの A*X*X+B*X+C が計算され、FNX(式) の値となります。
WHILE N<=M
PRINT N, FNF(N)
N=N+1
WEND
が、WHILE WEND 文です。
WHILE N<=M
・・・・・
WEND
は、Java の
while (N<=M) {
・・・・・
}
と同じです。
WHILE は通常繰り返しの回数が不明の時使います。例えば、
「自然数を入力して、その数の各桁の数字の和を求めなさい」という問題を、
INPUT "自然数:"; N
S=0
WHILE N>0
S=S+N-INT(N/10)*10
N=INT(N/10)
WEND
PRINT S
END
と解くような場合に使います。
例えば、N=12345 の時、
N を 10 で割った余りは 5
N を 10 で割って、 N=1234
N を 10 で割った余りは 4
N を 10 で割って、 N=123
N を 10 で割った余りは 3
N を 10 で割って、 N=12
N を 10 で割った余りは 2
N を 10 で割って、 N=1
N を 10 で割った余りは 1
N を 10 で割って、 N=0
という繰り返しを WHILE 文で捉える訳です。
私の BASIC の組み込み関数は
ABS(X) 絶対値関数
ATN(X) アークタンジェント関数
COS(X) コサイン関数
SIN(X) サイン関数
TAN(X) タンジェント関数
LOG(X) 対数関数
EXP(X) 指数関数
INT(X) 小数部分の切り捨て
SQR(X) 平方根
RND() 乱数
です。べきは2項演算子 ^ で計算できます。
次のプログラム例は、配列を使うものです。
REM 最大値
INPUT "データの個数N ";N
DIM A(N)
FOR J=1 TO N
INPUT A(J)
NEXT
X=A(1)
FOR J=2 TO N
IF A(J)>X THEN X=A(J)
NEXT
PRINT "最大値は";X
END
実行結果の例は
データの個数N 5
? 2
? 9
? 4
? 6
? 1
最大値は 9.0
です。
DIM A(N)
が、大きさ N の一次元配列の宣言です。変数は宣言しなくても(宣言する方法が
そもそも準備されていない)使えましたが、配列は使う前にその大きさを宣言する必要があります。この文を実行する時点で、計算でできるなら、N の部分は、式で良いです。
Java と異なり BASIC では、"(" と ")" を使います。
INPUT A(J)
で、配列 A の J 番目の要素にアクセスしています。
私の BASIC では、二次元の配列も使えます。次のプログラムは行列の積を計算するプログラムです。
REM 行列の積
INPUT "K,L,M=";K,L,M
DIM A(K,L), B(L,M), C(K,M)
REM 行列成分の入力
FOR I=1 TO K
FOR J=1 TO L
PRINT "A(";I;",";J;")=";
INPUT A(I,J)
NEXT
NEXT
FOR I=1 TO L
FOR J=1 TO M
PRINT "B(";I;",";J;")=";
INPUT B(I,J)
NEXT
NEXT
REM 積の計算
FOR I=1 TO K
FOR J=1 TO M
C(I,J) = 0
FOR IJ=1 TO L
C(I,J)=C(I,J)+A(I,IJ)*B(IJ,J)
NEXT
NEXT
NEXT
REM 結果の出力
FOR I=1 TO K
PRINT "C(";I;",J) ";
FOR J=1 TO M
PRINT C(I,J);
NEXT
PRINT
NEXT
END
実行結果は次のようになります。
K,L,M=2,2,2
A( 1.0 , 1.0 )= ? 5
A( 1.0 , 2.0 )= ? 3
A( 2.0 , 1.0 )= ? 4
A( 2.0 , 2.0 )= ? 6
B( 1.0 , 1.0 )= ? 3
B( 1.0 , 2.0 )= ? 4
B( 2.0 , 1.0 )= ? 6
B( 2.0 , 2.0 )= ? 2
C( 1.0 ,J) 33.0 26.0
C( 2.0 ,J) 48.0 28.0
二次元の配列の宣言は
DIM A(K,L), B(L,M), C(K,M)
のようにします。複数の配列をコンマで区切って一行に書いても良いです。Java と配列の表現形式が異なるので注意して下さい。アクセスは
C(I,J)=C(I,J)+A(I,IJ)*B(IJ,J)
のようにします。
そんなに難しいことはないはずです。
一行には、コロン : で区切って、
FOR J=1 TO M: JJ(J)=0: NEXT J
や
MM(I)=N: JJ(N)=1: KK(I-N+M)=1: LL(I+N-1)=1
や
IF S<1 THEN P=0:Q=1 ELSE P=1:Q=S
のように複数の命令が書けます。
INPUT 文は、
INPUT "S=";S
のように、" と " で囲われたプロンプトの文字列があれば、それをそのまま表示します。文字列がなければ、? を表示します。入力する変数や配列の要素が複数ある時は、コンマ , で区切ります。
INPUT 文に対するプロンプトの文字列は、最初にしか指定できません。
INPUT "S=";S;"T=";T
のような命令はエラーです。
INPUT "S=";S
INPUT "T=";T
と2行に書いて下さい。
PRINT 文は、" と " で囲われた文字列と式の値をコンマ , またはセミコロン ; で区切って、複数自由に表示できます。セミコロン ; の後の表示はスペースを一つおいて続けて表示されます。コンマ , の後の表示は次のタブ位置から表示されます。
PRINT NI;"回反復 近似解=";R
のように、PRINT 文がコンマ , またはセミコロン ; で終わっていなければ、表示の後、改行されます。
PRINT
と PRINT だけなら、改行だけが行われます。
PRINT USING "#.00" X
のように、USING を使って、書式を指定することができます。この場合は、小数点以下2桁必ず表示しなさいという指示です。X=3.00 でも 3.00 と表示します。
PRINT USING "#.##" X
は、小数点以下2桁表示しなさいという指示ですが、後ろの方の 0 は表示しません。
X=3.00 なら 3 と表示します。同様に、
PRINT USING "00000.00" X
とすれば、0 を補って、必ず整数部5桁、小数部2桁で表示します。
PRINT USING "#####.##" X
なら、不必要な 0 は表示されません。綺麗な表形式の表示が欲しいときに使います。
高等学校の数学の教科書には、複雑な PRINT USING 文が載っていますが、作るのが面倒だし、代用できるので、私の BASIC の PRINT USING 文は上で説明したものだけです。
数値計算のため(グラフィックス以外)の私の BASIC の仕様の説明は以上です。非常に単純で、覚えやすいものです。
次に Tiny Basic によるグラフィックスについて説明します。
平面グラフィックスのプログラムは高等学校の教科書からは一社を除いて
消えました。しかし、グラフィックスのプログラムは結果がはっきりしているので、
プログラミングの勉強には非常に有効です。
以下は、Tiny Basic のアプレット版では実行できません。
私のノートパソコンでは、Windows XP で、
Microsoft Internet Explorer Version 6.0 ですが、実行できません。
Window 2000 でも駄目です。
Eclipse で開発していますが、Eclipse 上では、
理由はわかりませんが実行できます。従って
Tiny Basic のアプリケーション版を使って下さい。
Java の RunTime をインストールして、TinyBasic.jar のアイコンを
ダブルクリックして下さい。試しに一回だけ使ってみるには、TinyBasic.jar のダウンロードをクリックして、保存ではなく、開くを実行して下さい。Tiny Basic のアプリケーション版が使えます。
グラフィックスを使うとき、最初に
SCREEN 3
と書いておきます。3 には最早意味はありませんが、このように書いておきます。これがあると 640 × 400 の大きさのウィンドウが開きます。座標系は、左上隅が原点 (0,0) で、X 座標は右向きが正で、Y 座標は下が正です。
線を描くには LINE 文を使います。
LINE (250,300)-(100,100),1
LINE (400,220)-(500,250),2,B
LINE (300,100)-(630,380),4,BF
のように使います。
LINE 文は
LINE (式1,式2)-(式3,式4),式5
の形式で使います。座標(式1,式2)と(式3,式4)の点を結ぶ線分を式5の色で引きます。更に、
LINE (式1,式2)-(式3,式4),式5,B
とすると、座標(式1,式2)と(式3,式4)の点を端点とする矩形を式5の色で描きます。また、
LINE (式1,式2)-(式3,式4),式5,BF
とすると、座標(式1,式2)と(式3,式4)の点を端点とする矩形を式5の色で塗りつぶします。LINE 文で、同じ色で描くときは、色の指定は
line (10,10)-(100,100),3,BF
line (150,150)-(100,100)
line (300,300)-(350,380),,BF
のように省略でき、すべて黄色で描きます。
色は
0 : Color(0.0f, 0.0f, 0.0f)
1 : Color(1.0f, 0.0f, 0.0f)
2 : Color(0.0f, 1.0f, 0.0f)
3 : Color(1.0f, 1.0f, 0.0f)
4 : Color(0.0f, 0.0f, 1.0f)
5 : Color(1.0f, 0.0f, 1.0f)
6 : Color(0.0f, 1.0f, 1.0f)
7 : Color(1.0f, 1.0f, 1.0f)
8 : Color(0.0f, 0.0f, 0.0f)
9 : Color(0.5f, 0.0f, 0.0f)
10 : Color(0.0f, 0.5f, 0.0f)
11 : Color(0.5f, 0.5f, 0.0f)
12 : Color(0.0f, 0.0f, 0.5f)
13 : Color(0.5f, 0.0f, 0.5f)
14 : Color(0.0f, 0.5f, 0.5f)
15 : Color(0.5f, 0.5f, 0.5f)
で、定義しています。最初の数値が赤、次が緑、最後が青の割合です。
例えば、
SCREEN 3
A = 0.1
PI = 4*ATN(1)
THETA=PI/4-ATN(1-A)
RHO=SQR(2-2*A+A*A)/SQR(2)
DIM X(4),Y(4)
X(1)= 1: Y(1)= 1
X(2)=-1: Y(2)= 1
X(3)=-1: Y(3)=-1
X(4)= 1: Y(4)=-1
FOR N=1 TO 40
LINE (320+150*X(1),200-150*Y(1))-(320+150*X(2),200-150*Y(2)),1
LINE (320+150*X(2),200-150*Y(2))-(320+150*X(3),200-150*Y(3)),1
LINE (320+150*X(3),200-150*Y(3))-(320+150*X(4),200-150*Y(4)),1
LINE (320+150*X(4),200-150*Y(4))-(320+150*X(1),200-150*Y(1)),1
FOR I=1 TO 4
G=RHO*( X(I)*COS(THETA)+Y(I)*SIN(THETA))
H= RHO*(-X(I)*SIN(THETA)+Y(I)*COS(THETA))
X(I)=G: Y(I)=H
NEXT
NEXT
END
を実行すると次のようになります。

この図は Tiny Basic のアプリケーション版で、実行したものです。
CIRCLE 文を使えば、円が描けます。
circle (300,200),100,4
circle (200,50),50,,F
のように使います。
CIRCLE 文は
circle (式1,式2),式3,式4
の形式で使い、座標(式1,式2)が中心で、半径が式3である円を式4の色で描きます。更に、
circle (式1,式2),式3,式4,F
の形式で、座標(式1,式2)が中心で、半径が式3である円を式4の色で塗りつぶします。
SCREEN 3
DEF FNX(S)=320+200*(COS(S)*COS(S)-A)/2
DEF FNY(S)=200-200*COS(S)*SIN(S)/2
DEF FNR(S)=200*SQR(A*A+(2*A+1)*COS(S)*COS(S))/2
A = 0.5
PI = 4*ATN(1)
FOR T=-PI/2 TO PI/2 STEP PI/50
CIRCLE (FNX(T),FNY(T)), FNR(T), 0
NEXT T
END
を実行すると次のようになります。

PSET 文を使って点を描くことも出来ます。PSET 文は
PSET (式1,式2),式3
の形式で使い、座標(式1,式2)の位置に式3の色で点を描きます。
SCREEN 3
DEF FNX(T)=320+200*SIN(3*T/2)*COS(T)
DEF FNY(T)=200-200*SIN(3*T/2)*SIN(T)
PI=4*ATN(1)
LINE (0,200)-(640,200),1
LINE (320,0)-(320,400),1
FOR T=0 TO 4*PI STEP PI/100
PSET(FNX(T),FNY(T)),4
NEXT T
END
を実行すると次のようになります。
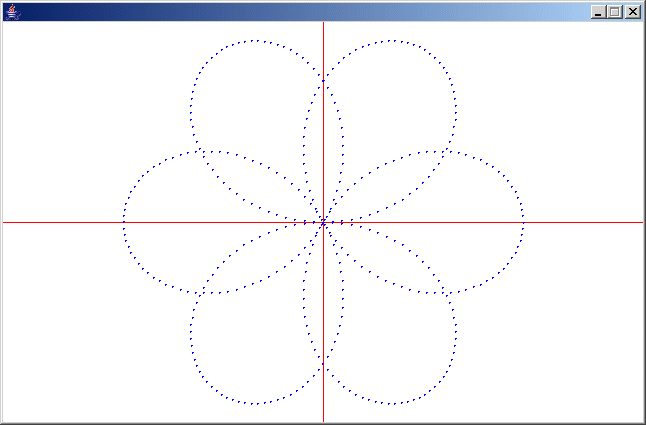
もう一つ、グラフィックスの例を挙げておきます。Cassini曲線
(2定点からの距離の積が一定の点の軌跡)を描くプログラムです。
screen 3
pi = 4 * atn(1)
a=100
for k= 20 to 160 step 10
for t=0 to 2*pi step pi/400
c2 = cos (2*t)
r = a*a*a*a*(c2*c2-1)+k*k*k*k
if r < 0 then goto 100
r = sqr (r)
s = a*a*c2 + r
if s < 0 then goto 100
s = sqr (s)
x = s*cos(t)
y = s*sin(t)
pset (320+x,200-y)
s = a*a*c2 - r
if s < 0 then goto 100
s = sqr (s)
x = s*cos(t)
y = s*sin(t)
pset (320+x,200-y)
100 next
next
end
実行すると次のようになります。
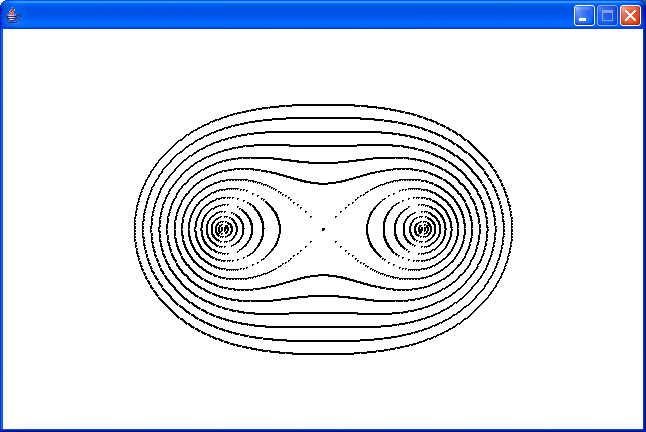
この図は Tiny Basic のアプリケーション版で、実行したものです。
















