HUMMINGBIRD.EXE を立ち上げてみましょう。
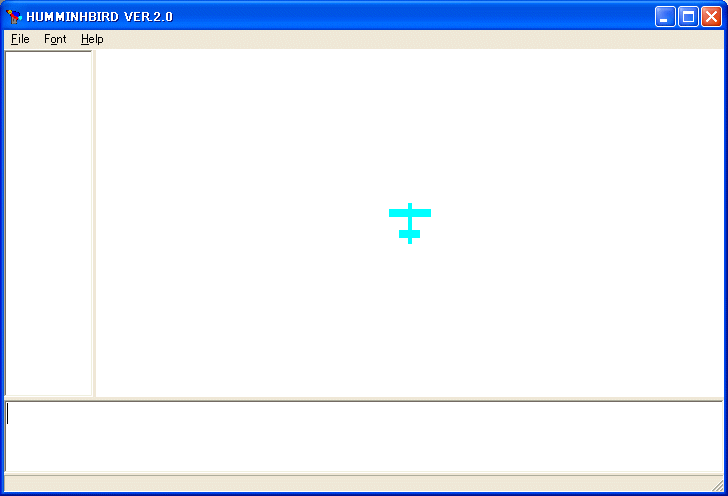
画面が三つの領域に分かれています。黒い画面がタートルが線画を描くキャンバスです。画面の真中にいる飛行機が一匹目のタートルです。下の領域がタートルに対する命令を打ち込む領域です。左側の領域がPRINT命令の結果やLISTING命令の結果が表示される領域です。それぞれの大きさを変化させることも出来ます。
下の領域にHTと打ち込みEnterキーを押すと飛行機が消えます。
HT 命令は
<![CDATA[
HT
]]>
の形式で使い、HideTurtle の省略形で、飛行機を見えないようにします。
STと打ち込みEnterキーを押すと飛行機が現れます。
ST 命令は
<![CDATA[
ST
]]>
の形式で使い、ST は ShowTurtle の省略形で、飛行機を見えるようにします。
HUMMINGBIRD ではタートルと呼ばれる飛行機（後でもう一つのタートルであるヘリコプターが出てきます）に命令することにより絵を描きます。タートルに対する命令は「消えろ」、「現れろ」、「前進せよ」、「右に回転せよ」、「ペンをあげろ」とか「ペンを降ろせ」といった命令です。これらの命令を英語の略字で指示します。飛行機は最初は画面の中央にいます。HUMMINGBIRD は ENTER キーを押したらその行の命令達（複数の命令を１行に書くことができます）を実行します。HT と打ち込み、ENTER キーを押せば、飛行機が消えます。ST と打ち込み、ENTER キーを押せば、飛行機が現れます。以下、Enterキーを押すという指示は省略します。
命令はすべて半角文字で指示します。この HUMMINGBIRD は大文字と小文字を区別しません。従って、例えば、HT命令はhtでもHtでもhTでもいいです。CSと打ち込むと絵を消し、飛行機は原点に戻ります。
CS 命令は
<![CDATA[
CS
]]>
の形式で使い、ClearScreen の省略形です。
初期状態では飛行機は三次元空間の原点（0,0,0）に居て、飛行機が見えています。XY 平面が画面で、原点は画面の中央です。Z 軸は画面に垂直で手前が正の方向です。タートルはペンを下ろしています。移動すると線を描きます。ペンを上げると移動しても線を描きません。
CS命令を実行して、初期状態に戻してください。飛行機は原点でXY平面に平行でY軸の正の向きを向いて背中をZ軸の正の方向に向けています。色々確かめていると分かってくると思いますので最初はあまり気にしないで下さい。FD 100 を実行します。（即ち、下の領域に FD 100 と打ち込みEnterキーを押す。FD と 100 の間には半角スペースが必要です。全角スペースではエラーです。）
飛行機が100単位だけ前進します。
FD 命令は
<![CDATA[
FD 数式
]]>
の形式で使い、飛行機が数式の値だけ前進します。副作用として、ペンが下りていれば、線を描きます。FD は ForwarD の省略形です。
RT 90 を実行します。（即ち、下の領域に RT 90 と打ち込みEnterキーを押す。RT と 90 の間には半角スペースが必要です。全角スペースではエラーです。）
飛行機が右に90度回転します。
RT 命令は
<![CDATA[
RT 数式
]]>
の形式で使い、飛行機が数式の値だけ右に回転します。単位は度です。RT は
RighT の省略形です。
FD 100 RT 90 を四回繰り返すと正方形を描いて元の位置に戻ります。
BK 命令は
<![CDATA[
BK 数式
]]>
の形式で使い、飛行機が数式の値だけ後退します。副作用として、ペンが下りていれば、線を描きます。BK は BACK の省略形です。
LT 命令は
<![CDATA[
LT 数式
]]>
の形式で使い、飛行機が数式の値だけ左に回転します。単位は度です。
、LT は LefT の省略形です。
PU 命令は
<![CDATA[
PU
]]>
の形式で使い、飛行機がペンを上げます。PU は PenUp の省略形です。
PU LT 90 FD 100 PD を実行します。
PD 命令は
<![CDATA[
PD
]]>
の形式で使い、飛行機がペンを下ろします。PD は PenDown の省略形です。
FD 100 RT 120 FD 100 RT 120 FD 100 RT 120 を実行します。
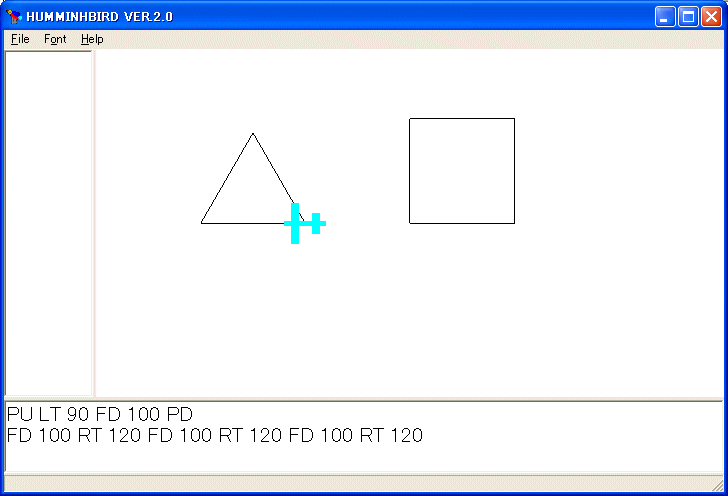
以上のように FD, BK, RT, LT, PU, PD の６個の命令を覚えれば、任意の線画が描けます。しかし、これだけでは複雑な図を描くのは大変です。繰り返し構造があるとか数式で表現できるといった数学的な規則のある図形ならもっと簡単に描くことが出来ます。そのために、制御構造や関数や手続きが HUMMINGBIRD に準備されています。それらを以下で学びます。
同じことを何回も繰り返すのは大変です。REPEAT 命令を使うと楽が出来ます。
<![CDATA[
REPEAT 4 [FD 100 RT 90]
]]>
とすれば、[ と ] の間の命令 FD 100 RT 90 を 4 回繰り返します。従って、この命令だけで正方形を描きます。CS REPEAT 4 [FD 100 RT 90] を実行します。
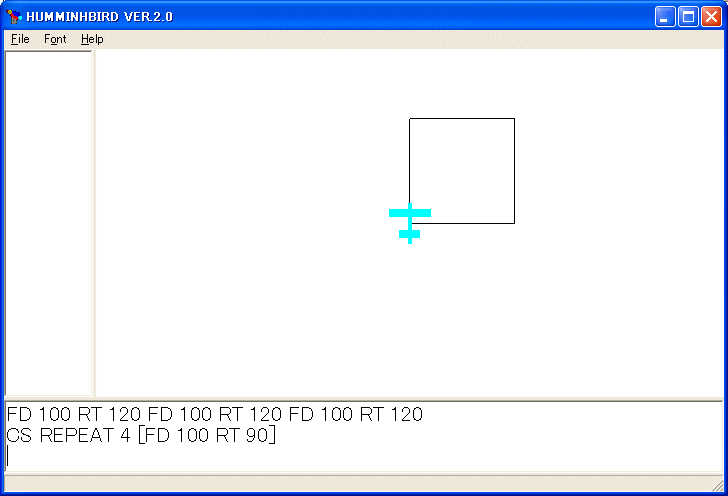
REPEAT 命令は
<![CDATA[
REPEAT 数式 [ 命令の列 ]
]]>
の形式で使い、命令の列を数式の値の回数繰り返します。
■■■■■■■■■■
● HUMMINGBIRD が命令を理解する方法 ●
HUMMINGBIRD が命令を理解する方法を少し述べてみます。HUMMINGBIRD は ENTER キーが押されると、その行を最初から一文字づつ調べて「トークン」と呼ばれる意味を持った単語に分解します。
<![CDATA[
REPEAT 4 [FD 100 RT 90]
]]>
であれば、まず
R を見つけ、 R が英字ですから、以下、英字または数字またはアンダーバー _ が続く間は一つながりの意味を持っているものだと解釈し、スペースが出てくる REPEAT までを抜き出し、 REPEAT を最初のトークンだと認識します。トークンの区切りである次の半角スペースをとばして、次の 4 を見ると、 4 は数字ですから、これからは数が表現されていると認識し、数字や . を一続きのトークンだと思って調べます。この場合、 4 の次がスペースですから数を表すトークンとして 4 を抜き出します。トークンの区切りであった次の半角スペースをとばして、次の [ を見ると、 [ は記号ですから、直ちに [ をトークンとして認識します。次の F を見て、スペースまでの FD をトークンとします。このようなことを繰り返して、
以下 100 と RT と 90 と ] というトークンを抜き出します。このようにトークンを抜き出すと同時に、HUMMINGBIRD はトークン列でどのような命令がなされているかを理解しようとします。まず最初のトークン REPEAT より「 REPEAT 式 [ 命令の並び ] 」の形式の命令があるはずだと認識します。次のトークン列は繰り返しの回数を指示する式を表現するトークン列であるはずだと理解しています。今の場合 4 と数を表すトークンですから、繰り返しの回数は 4 回だと認識します。次のトークンは [ で、 ] のトークンが出てくるまでのトークン列が繰り返すべき命令の並びを表現しているはずだと知っています。 [ と ] の間には FD 100 RT 90 があります。 FD のトークンを見て、「FD 式」の形式の命令だと認識します。次のトークン列は飛行機が前進する距離を指示する式を表現するトークン列であるはずだと理解しています。今の場合 100 と数を表すトークンですから、飛行機が前進する距離は 100 だと認識します。そして、次に RT のトークンを見て、「 RT 式」 の形式の命令だと認識します。次のトークン列は飛行機が右に回転する角度を指示する式を表現するトークン列であるはずだと理解しています。今の場合 90 と数を表すトークンですから、飛行機が右に回転する角度は 90 だと認識します。このように認識して、「飛行機を 100 前進し、 90 度右に回転し」を 4 回繰り返します。
HUMMINGBIRD の持っているこのような解釈とトークン列が食い違っていれば、エラーメッセージが出ます。例えば、
<![CDATA[
REPEAT 4 [FD 100 RT 90]
]]>
と打ち込むべきところを FD と 100 との間のスペースを取って
<![CDATA[
REPEAT 4 [FD100 RT 90]
]]>
と打ち込んで見ると
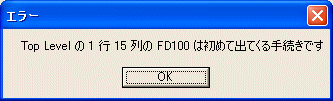
「Top Level の 1 行 15 列の FD100 は初めて出てくる手続きです」という、 FD100 という命令は理解できないというエラーメッセージが出ます。「Top Level」というのはコマンドライン（下の領域）でエラーが見つかったという意味です。 行番号は HUMMINGBIRD に何行命令を打ち込んだかによって変わります。FD と 100 という二つのトークンとしてではなく、 FD100 という一つのトークンとして認識しています。OK ボタンをクリックして下さい。HUMMINGBIRD はエラーのあった行は無視して、新たに次の行から解釈を始めます。次の行に正しい命令を打ち込めば良いです。反応しない場合には、カーソルを移動して、もう一度実行してみて下さい。それで、多分うまくいきます。
また、
<![CDATA[
REPEAT 4 [FD 100 RT 90]
]]>
は 4 と [ の間を詰めて
<![CDATA[
REPEAT 4[FD 100 RT 90]
]]>
としても、見やすいように半角スペースを追加して
<![CDATA[
REPEAT 4 [ FD 100 RT 90 ]
]]>
としても、あいだに ENTER を押して、複数行にして
<![CDATA[
REPEAT 4 [
FD 100 RT 90
]
]]>
としても良いです。
■■■■■■■■■■
正三角形、正五角形、正六角形、正七角形、星型正五角形、星型正七角形など色々描いて見ましょう。
正方形を何個も描きたい時、何時も REPEAT 4 [FD 100 RT 90] と打ち込むのは大変です。コンピュータに正方形の描き方を教えてやりましょう。TO SHIKAKU と打ち込みます。
手続きや関数を定義する為のダイアログボックスが開きます。
ダイアログボックスのメモの一行目に TO SHIKAKU と書いてあります。二行目に REPEAT 4 [FD 100 RT 90] と打ち込み、三行目に END と打ち込みます。ダイアログボックスのメモが
<![CDATA[
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
]]>
となっていることを確かめたら、OK ボタンを押します。
定義の最後には必ず END と打ち込んでください。END が手続きや関数の定義の終了の印で、必ず必要です。
■■■■■■■■■■
● 手続きの定義の仕方 ●
SHIKAKU という名前の手続きを定義するには、コマンドラインに（即ち、下側の領域に） TO SHIKAKU と打ち込みます。手続きや関数を定義する為のダイアログボックスが開きます。 ダイアログボックスのメモの一行目に TO SHIKAKU と書いてあります。二行目に REPEAT 4 [FD 100 RT 90] と打ち込み、三行目に END と打ち込みます。ダイアログボックスのメモは
<![CDATA[
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
]]>
となります。手続きの定義は、
<![CDATA[
TO 手続き名
命令
・・・
命令
END
]]>
の形式で定義します。手続きの定義の最後は END で終わらなくてはなりません。
ダイアログボックスの下のほうにある OK と描かれたボタンを押します。これで SHIKAKU という手続きをコンピュータが理解するようになります。
コマンドラインに（即ち、下側の領域に）
<![CDATA[
TO SHIKAKU
REPART 4 [FD 100 RT 90]
END
]]>
と打ち込むのではありませんので、くれぐれも間違わないようにしてください。
■■■■■■■■■■
LISTING 命令を実行してみます。左の領域に SHIKAKU と表示されるはずです。
SHIKAKU という命令をコンピュータが覚えました。
LISTING 命令は、
<![CDATA[
LISTING
]]>
の形式で使い、HUMMINGBIRD が覚えている手続きや関数の名前を左の領域に表示します。
CS 命令を実行し、初期画面に戻し、SHIKAKU と打ち込んでEnterキーを押して下さい。
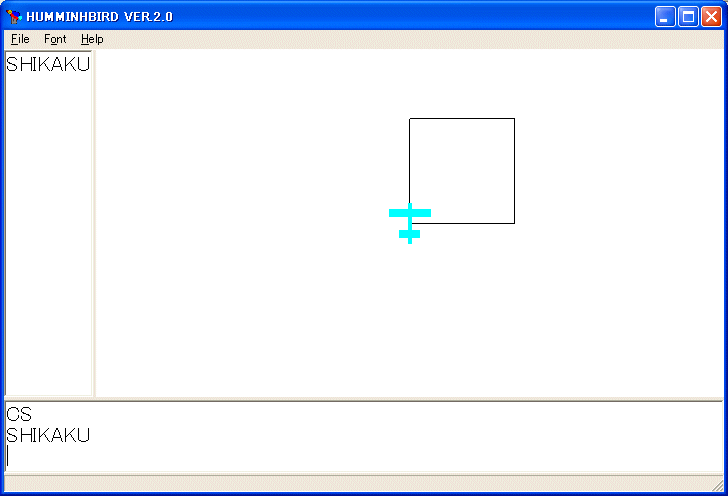
正方形が描かれたはずです。エラーが表示されたら、何と言っているか良く読んでください。
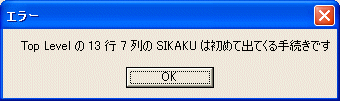
例えば SHIKAKU と打ち込んだつもりが SIKAKU の場合は、「OK」のボタンを押し、もう一度、次の行に、SHIKAKU と打ち直せば良いです。
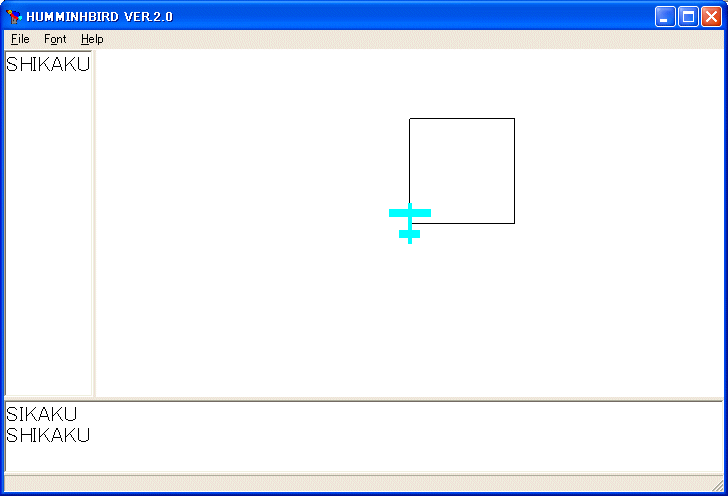
例えば、
<![CDATA[
TO SHIKAKU
REPAET 4 [FD 100 RT 90]
END
]]>
と定義して、SHIKAKU を実行すると次のようなエラー表示があります。
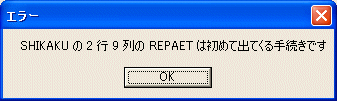
SHIKAKU の定義の中にエラーがあると言っているので、「OK」のボタンを押し、コマンドラインにもう一度 TO SHIKAKU と入力し、
ENTER キーを押します。コンピュータに教えた SHIKAKU の定義の書かれたダイアログボックスが出てきますから、
間違いを直して、
OK ボタンを押して、やり直してください。この自分で定義した命令も FD や RT のような組み込みの手続きと同様に使うことが出来ます。
<![CDATA[
REPEAT 4 [SHIKAKU RT 90]
]]>
と実行して下さい。
原点を中心に正方形を90度づつ回転しながら4個描いたはずです。
■■■■■■■■■■
● 画面を拡大・縮小したり、ダイアログボックスを表示して絵が消えた場合 ●
本来なら絵が消えないようにプログラミングすべきですが、今のところ方法が分かりません。REPAINT 命令を打ち込んで下さい。
REPAINT 命令は
<![CDATA[
REPAINT
]]>
の形式で使い、既に描かれている画面を再描画します。
絵が復元できます。
■■■■■■■■■■
毎回同じ大きさの正方形では面白くありません。TO SHIKAKU と打ち込んでください。
HUMMINGBIRD を新たに立ち上げたのでなければ、
<![CDATA[
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
]]>
と書かれたダイアログボックスが現れるはずです。次のように修正します。
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
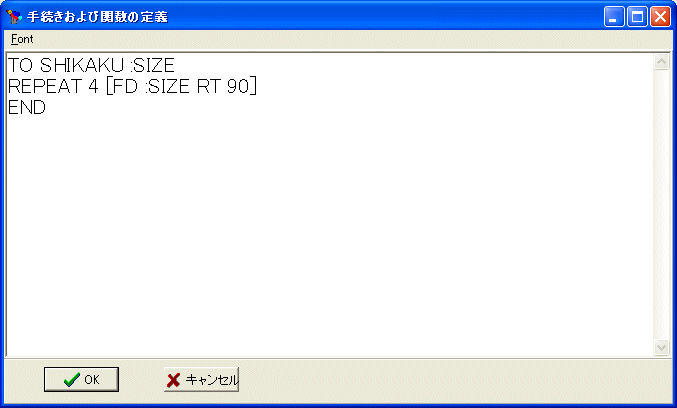
正しく打ち込めたことを確かめて、OK ボタンを押します。このように、SHIKAKU を書き直すと古い引数の無い SHIKAKU はなくなります。名前だけで記憶していて、手続きや関数の多重定義はできません。
■■■■■■■■■■
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
というプログラムを示すと一行目から全部改めて打ち込んで
<![CDATA[
TO SHIKAKU
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
となっている人がよくいます。これはエラーになります。初めて TO SHIKAKU を実行したときもコンピュータが作ってくれる TO SHIKAKU を利用して、ダイアログボックスのメモの内容を
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
としてください。
また、すべてを一行にして、
<![CDATA[
TO SHIKAKU :SIZE REPEAT 4 [FD :SIZE RT 90] END
]]>
とするのも間違いです。
HUMMINGBIRD は基本的には行は関係ない言語ですが、
手続きの定義の一行目には、TO と手続きの名前と仮引数の並びしか書かないようにして下さい。理由はまだ出てきていないのですが、HUMMINGBIRD には代入文があり、変数名 = 式の形式で使います。例えば、
<![CDATA[
TO SHIKAKU :SIZE :X = :SIZE/2 REPEAT 4 [FD :X RT 90] END
]]>
のような手続きが考えられます。この手続きは引数の半分の大きさの正方形を描きます。このような手続きを HUMMINGBIRD が認識するとき、SHIKAKU の引数が何であるか調べるとき、:X が引数でないことを認識するためには = まで読んでみる必要があります。引数でないことが分かると読みを :X まで戻す必要があります。このようなことを可能にするためには HUMMINGBIRD 自身のプログラムが複雑になり、見た目もきれいではないので、手続きの定義の一行目には、TO と手続きの名前と仮引数の並びしか書かないように HUMMINGBIRD を制限しています。
即ち、手続きの定義は、
<![CDATA[
TO 手続き名 引数の並び
命令
・・・
命令
END
]]>
の形式で定義します。「TO 手続き名 引数の並び」は１行に記述します。この行には命令は書いてはいけません。手続きの最後は END だけの行にします。
さらに、SHIKAKU を定義するとき、SHIKAKU に引数があるからといって、コマンドラインで
<![CDATA[
TO SHIKAKU :SIZE
]]>
と入力する人がいますが、仮引数を付けると、SHIKAKU を定義した後、エラーメッセージがでます。
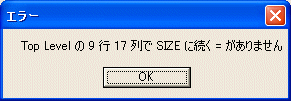
TO SHIKAKU を処理した後、:SIZE を読み込んだが、変数だけで、これでは、何をすればいいか分からないと言っています。この場合は、単にエラーメッセージを無視すればいいです。
■■■■■■■■■■
CS 命令で、画面を初期化し、SHIKAKU 50 と打ち込みます。
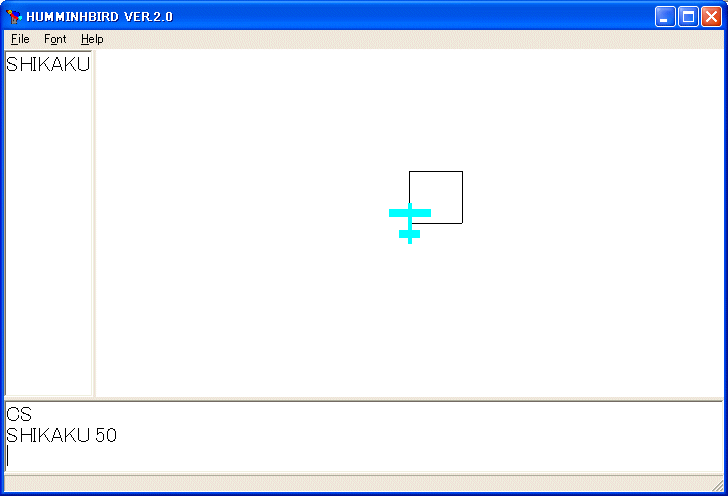
50 単位の正方形を描くはずです。
HUMMINGBIRD は SHIKAKU というトークンを見つけると SHIKAKU という名前の手続きの定義を探します。
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
という定義を見つけます。SHIKAKU には :SIZE という引数が１つあることを見つけ、コマンドラインの次のトークンを調べます。50 を見つけます。SHIKAKU の引数 :SIZE が 50 だと認識します。SHIKAKU の定義の次の行
<![CDATA[
REPEAT 4 [FD :SIZE RT 90]
]]>
を実行します。このとき、変数 :SIZE に出会うと SHIKAKU の引数 :SIZE が 50 だったので、:SIZE を 50 で置き換えて実行します。（正確に言うと、局所変数のリストに、:SIZE の値を 50 で登録し、変数 :SIZE が出てくるたびに、局所変数のリストを探し、:SIZE の値を求めます。従って、:SIZE の値を、手続きの中で、代入文で変更することもできます。）従って、一辺 50 の正方形を描きます。次の行に制御が移ります。次の行が END なので、SHIKAKU 50 の実行は終了します。HUMMINGBIRD は、手続きの中で END か STOP に出会うとその手続きを終了します。
■■■■■■■■■■
● 作ったプログラムを保存したい時 ●
せっかく覚えさせた手続きも HUMMINGBIRD を終了すれば無くなります。ファイルに保存しておけば、次に読み込んで使うことが出来ます。File メニューの Save で保存できます。ファイル名は何でも良いです。拡張子にも制限はありません。File メニューの Open でファイルから手続きや関数の定義を読み込むことが出来ます。保存したファイルはテキストファイルで、単に
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
と書いてあるだけです。したがって、HUMMINGBIRD で定義しなくても、メモ帳などで、
<![CDATA[
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
]]>
というファイルを作って、読み込むことでも、手続きや関数を覚えさせることが出来ます。また、手続きや関数の定義は一つのファイルに複数続けて定義しても良いです。読み込んだ手続きや関数はそのまま使うことが出来ます。
どのような手続きや関数が読み込まれたかは LISTING 命令で確かめることが出来ます。
■■■■■■■■■■
三角形を描く手続きを定義しましょう。
<![CDATA[
TO SANKAKU :SIZE
REPEAT 3 [FD :SIZE RT 120]
END
]]>
で定義できます。いったん定義した手続きは自由に使うことが出来ます。
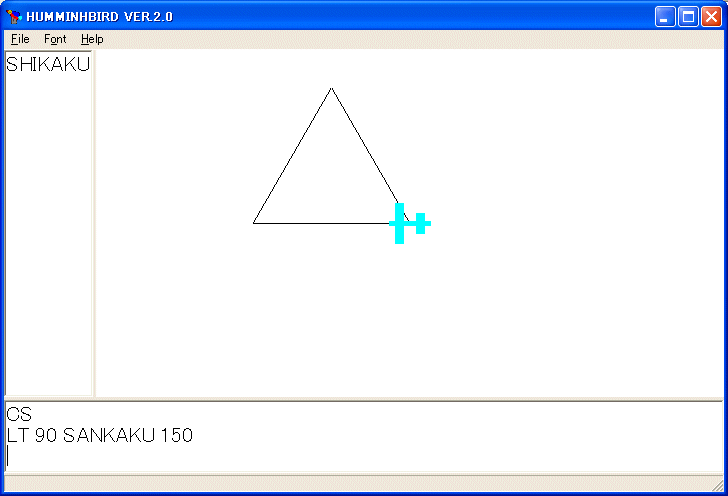
家を描く手続きを定義しましょう。正方形と正三角形の手続きを続けて
<![CDATA[
TO HAUSE :SIZE
SHIKAKU :SIZE SANKAKU :SIZE
END
]]>
で良いと思ったかも知れません。しかし駄目です。HAUSE 100 としてみましょう。
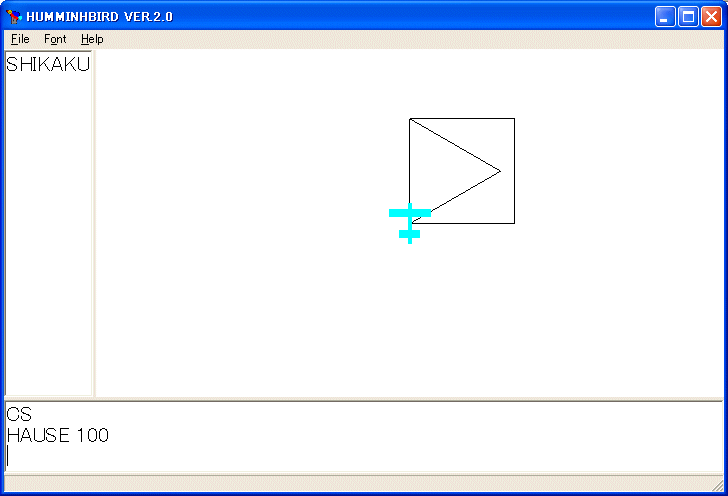
手続きの描き初めと描き終わりのタートルの状態（位置と姿勢）に注意する必要があります。修正して、
<![CDATA[
TO HAUSE :SIZE
SHIKAKU :SIZE FD :SIZE RT 30 SANKAKU :SIZE
END
]]>
とすれば、家を描きます。
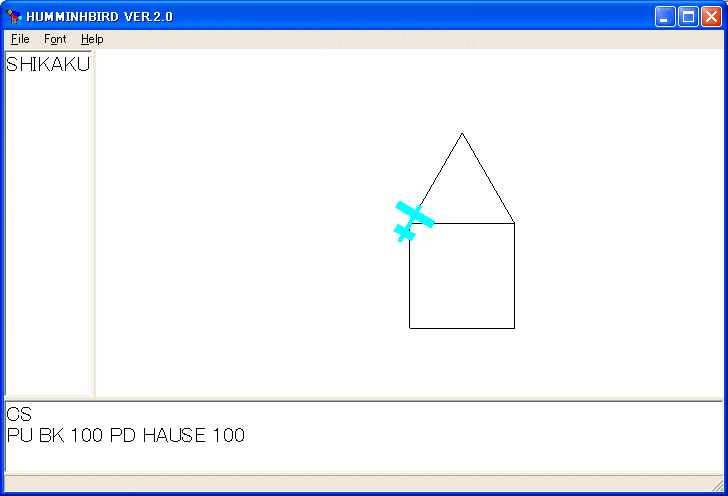
しかし、使い方にも拠りますが、次のように定義するほうが使い易い手続きになります。
<![CDATA[
TO HAUSE :SIZE
SHIKAKU :SIZE FD :SIZE RT 30 SANKAKU :SIZE LT 30 BK :SIZE
END
]]>
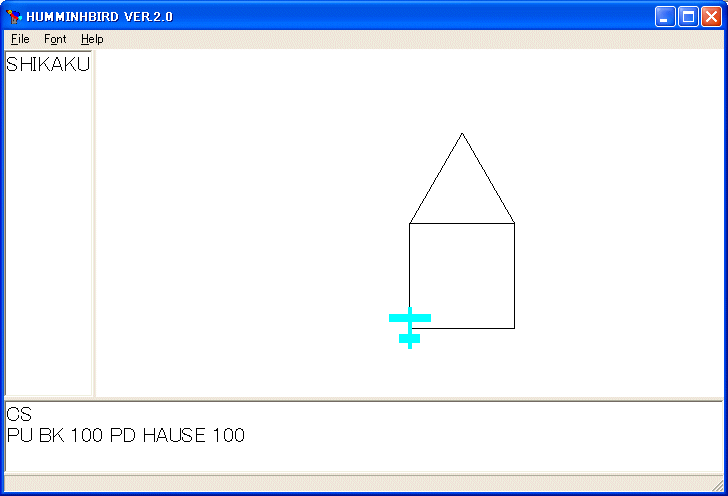
多くの場合、描きはじめと同じ状態にタートルが戻るように手続きを定義しておくと使い易い手続きになる場合が多いようです。勿論、コッホ曲線のような例外もあります。
■■■■■■■■■■
● 作った図形を印刷したい時 ●
HUMMINGBIRD で描いた画面を印刷したい時は、メニューの File の Print を実行します。
■■■■■■■■■■
背景を SetBackColor 命令で変えることができます。
SetBackColor 命令は
<![CDATA[
SETBACKCOLOR 数式1 数式2 数式3
]]>
の形式で使い、数式1 の値が赤の明るさ、数式2 の値が緑の明るさ、数式3 の値が青の明るさを 0 から 1 の実数値で指示します。即ち、SetBackColor 命令の引数は RGB 形式で色を指定します。1 1 1 は白、 0 0 0 は黒、 1 0 0 は赤、 0 1 0 は緑、 0 0 1 は青、 1 1 0 は黄色、 0.5 0.5 0.5 は灰色などです。
SetColor 命令でペンの色を変えることができます。
SetColor 命令は
<![CDATA[
SETCOLOR 数式1 数式2 数式3
]]>
の形式で使い、数式1 の値が赤の明るさ、数式2 の値が緑の明るさ、数式3 の値が青の明るさを 0 から 1 の実数値で指示します。即ち、SetColor 命令の引数は RGB 形式で色を指定します。1 1 1 は白、 0 0 0 は黒、 1 0 0 は赤、 0 1 0 は緑、 0 0 1 は青、 1 1 0 は黄色、 0.5 0.5 0.5 は灰色などです。
また、SetLineWidth 命令で線の大きさを変えることができます。
SetLineWidth 命令は
<![CDATA[
SETLINEWIDTH 数式
]]>
の形式で使い、数式の値は線の大きさを指示する正の整数値です。デフォルトは 1 です。但し、線の大きさは、既に描いている図形もすべて同じ大きさになります。ここの図形の線の大きさは指定できません。
<![CDATA[
TO SHIKAKU :SIZE
SETCOLOR 1 0 0 FD :SIZE RT 90
SETCOLOR 0 1 0 FD :SIZE RT 90
SETCOLOR 0 0 1 FD :SIZE RT 90
SETCOLOR 1 1 0 FD :SIZE RT 90
END
]]>
と SHIKAKU の定義を変えると
<![CDATA[
SETLINEWIDTH 4
SHIKAKU 150
]]>
を実行すると
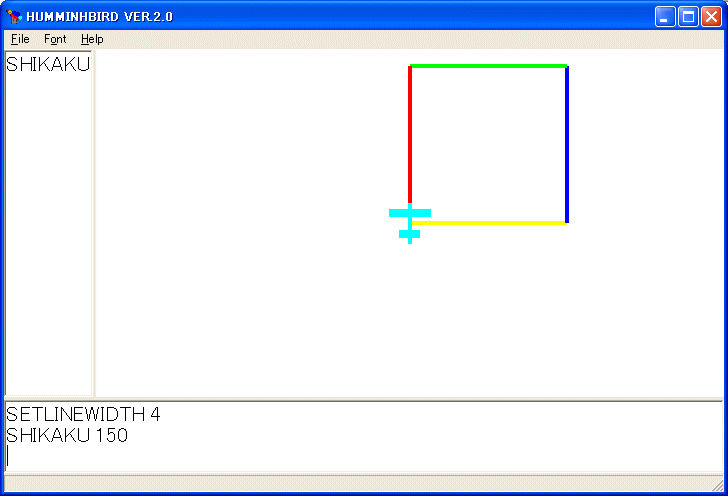
となります。
繰り返しをさせるには、現代的なプログラミング言語では再帰呼び出しという手法がよく使われます。効率が悪いと昔は嫌われましたが、コンピュータの性能が良くなった現代は積極的に使うべきです。慣れれば、見やすいプログラミングが出来ます。TO POLY と打ち込んで下さい。ダイアログボックスのメモに次のように打ち込みます。
<![CDATA[
TO POLY :SIZE :ANGLE
FD :SIZE RT :ANGLE
POLY :SIZE :ANGLE
END
]]>
と打ち込み、OK ボタンを押して下さい。:SIZE や :ANGLE は命令（普通は手続きといいます） POLY の引数といいます。引数をもつ手続きを定義するときでも TO POLY でいいです。TO POLY :SIZE :ANGLE として呼び出すと後で文句を言います。さて、 POLY 50 60 を実行して下さい。50 単位の正六角形を描き続きます。Esc キーを押して下さい。すぐには停止しないかも分かりませんが、Esc キーを何度か押すと描くのを停止します。
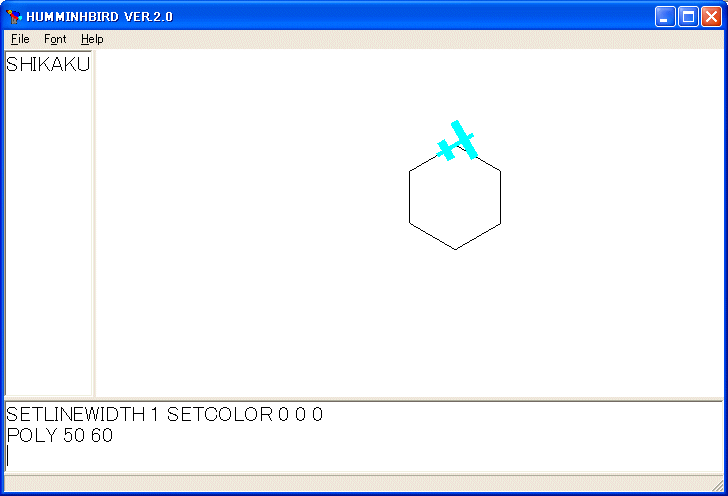
POLY という命令は次のように実行します。POLY 50 60 という命令をされたコンピュータは POLY の定義を調べて、POLY が二つの引数 :SIZE と :ANGLE を持つことを知り、:SIZE に 50 を :ANGLE に 60 を割り当てます。次に、POLY の定義の本体を順に調べていきます。FD :SIZE という命令があります。:SIZE には 50 が割り当てられているので 50 だけ前進します。次に、RT :ANGLE という命令があります。:ANGLE には 60 が割り当てられているので、右に 60 度回転します。次は、POLY :SIZE :ANGLE という命令です。:SIZE には 50 が :ANGLE には 60 が割り当てられていますから、POLY 50 60 を実行しなければなりません。コンピュータは再び POLY の定義を調べて、上と同じことを実行します。このようなメカニズムで POLY 50 60 は 50 単位の正六角形を描き続けます。停止するには、Esc キーを押す必要があります。再帰呼び出しというのは、POLY の定義をするのに POLY を使っていることによります。頭山的ともいいます。落語の頭山からきています。数学では再帰という言葉が使われます。代表例はヒボナッチ数列の定義です。
しかし、この POLY のような無限ループに陥る単なる繰り返しに過ぎないプログラムを再帰を使ってプログラムするのは勧められません。後で、POLY を停止するようにするための方法を示します。
HUMMINGBIRD は自分自身の関数を定義することも出来ます。最大公約数を計算する関数を定義して見ましょう。TO GCD を実行して下さい。
<![CDATA[
TO GCD :A :B
IF :B == 0 [OP :A]
OP GCD :B :A % :B
END
]]>
と定義してください。有名なユークリッドの互除法のアルゴリズムです。間違いがないことを確かめたら、OK ボタンを押します。関数は単独では使えません。
<![CDATA[
PRINT GCD 24 18
]]>
を実行して下さい。
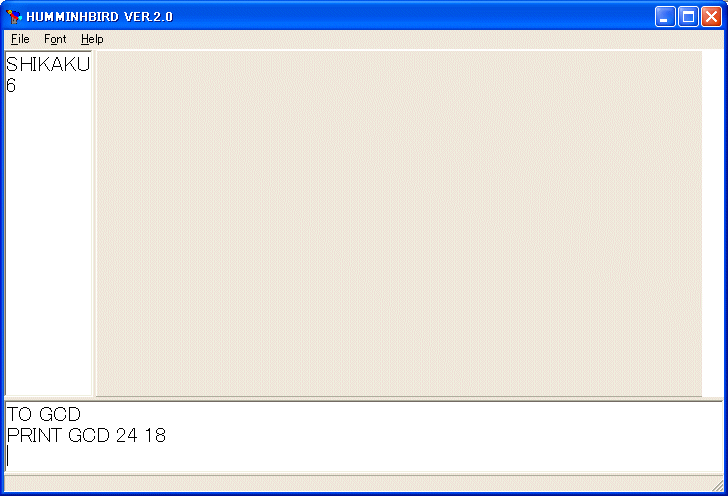
6 が左側の領域に表示されたはずです。PRINT GCD 24 18 と命令されるとコンピュータはGCD の定義を調べます。GCD は :A と :B の二つの引数を持っています。:A に 24 を :B に 18 を割り当てます。次の行は IF :B == 0 [OP :A] です。
IF 文は二通りの形式があります。
<![CDATA[
IF 条件式 [ 命令の並び ]
]]>
の形式の場合は、条件式が真であれば、命令の並びを実行します。IF 文が複数行になるときには、
<![CDATA[
IF 条件式 [
命令の並び
]
]]>
のように最初の[は条件式の後に（同じ行に）続けて下さい｡そのうち直しますが、今はこれが仕様だと思って下さい｡この方がプログラムが見やすいですから｡
二つ目の形式は
<![CDATA[
IF 条件式 [ 命令の並び ] [ 命令の並び ]
]]>
です。この場合は、条件式が真であれば、最初の命令の並びを実行し、偽であれば、二番目の命令の並びを実行します。IF 文が複数行になるときには、
<![CDATA[
IF 条件式 [
手続きの並び
][
手続きの並び
]
]]>
のように最初の[は条件式の後に（同じ行に）続け、二番目の[は最初の[と同じ行に続けて下さい｡そのうち直しますが、今はこれが仕様だと思って下さい｡この方がプログラムが見やすいですから｡
● これらの制御構造は好きなだけネストできます。
今の場合、条件式は :B == 0 です。:B に 0 が割り当てられていれば真、そうでなければ偽になります。
条件式は、関係演算子と論理演算子を組み合わせて作ります。関係演算子には、==, !=, >, <, >=, <= が準備されています。
<![CDATA[
● 数式1 == 数式2
== の両辺の値が等しければ真、そうでなければ偽です。
● 数式1 != 数式2
!= の両辺の値が等しくなければ真、そうでなければ偽です。
● 数式1 > 数式2
数式1 の値が数式2 の値より大きければ真、そうでなければ偽です。
● 数式1 < 数式2
数式1 の値が数式2 の値より小さければ真、そうでなければ偽です。
● 数式1 >= 数式2
数式1 の値が数式2 の値より大きいか等しければ真、そうでなければ偽です。
● 数式1 <= 数式2
数式1 の値が数式2 の値より小さいか等しければ真、そうでなければ偽です。
]]>
更に、論理演算子として、&&, ||, ! が準備されています。
<![CDATA[
● (条件式1) && (条件式2)
条件式1 と条件式2 の論理積を取ります。優先順位は *, /, % と同じです。
● (条件式1) || (条件式2)
条件式1 と条件式2 の論理和を取ります。優先順位は二項演算子 +, - と同じです。
● !(条件式)
条件式の論理否定を取ります。優先順位は単項演算子 +, - と同じです。
]]>
今の場合、:B には 18 が割り当てられているので、この IF 文では何もしません。次の行は OP GCD :B :A % :B です。OP 命令は GCD :B :A % :B の値をこの関数 GCD の値として関数 GCD の実行を終了せよという命令です。即ち、GCD 24 18 の値として GCD 18 24 % 18 を返せと定義しています。% は余りを取る演算子です。24 % 18 は 24 を 18 で割った余り 6 になります。従って、GCD 18 6 を計算して、その値が GCD 24 18 であると定義しています。コンピュータは GCD 18 6 を計算するために、GCD の定義を再び調べます。今度は :A に 18 を :B に 6 を割り当てます。:B には 0 が割り当てられていませんから、今度は GCD 18 6 の値は GCD 6 0 であると指示されます。再びコンピュータは GCD の定義を調べます。今度は :A には 6 が :B には 0 が割り当てられます。二行目の IF :B == 0 [OP :A ] の条件式 :B == 0 が今度は真になります。OP :A が実行できます。
OP 命令は
<![CDATA[
OP 数式
]]>
の形式で使い、数式の値をその関数の値として、関数の実行を終了します。
従って、
:A に割り当てられている 6 を GCD 6 0 の値として関数の実行を終わります。従って、GCD 24 18 = GCD 18 6 = GCD 6 0 = 6 として、GCD 24 18 の値 6 が求まりました。PRINT GCD 24 18 は GCD 24 18 の値 6 を左の領域に表示します。
PRINT 命令は
<![CDATA[
PRINT 数式
]]>
の形式で使い、数式の値を左の領域に表示します。
算術演算子には、+, -, *, /, % が準備されています。
<![CDATA[
● + 数式
単項演算子 + です。あってもなくても同じです。
● - 数式
単項演算子 - です。数式の値に -1 を掛ける。
● 数式1 * 数式2
数式1 の値と数式2 の値の積がその値となる。
優先順位は /, %, && と同じです。二項演算子 +, - より優先されます。
● 数式1 / 数式2
数式1 の値と数式2 の値の商がその値となる。
優先順位は *, %, && と同じです。二項演算子 +, - より優先されます。
● 数式1 % 数式2
数式1 の整数値を数式2 の整数値で割った余りがその値となる。
優先順位は *, /, && と同じです。二項演算子 +, - より優先されます。
● 数式1 + 数式2
数式1 の値と数式2 の値の和がその値となる。
優先順位は二項演算子 -, || と同じです。
二項演算子 *, /, %, && の方が優先されます。
● 数式1 - 数式2
数式1 の値と数式2 の値の差がその値となる。
優先順位は二項演算子 +, || と同じです。
二項演算子 *, /, %, && の方が優先されます。
例：
2 * 3 - 5 と 2 * (3 - 5) はそれぞれ 1 と -4 です。
● ( と )
( と ) を使うことで演算子の優先順序を変更できます。
]]>
今度は最小公倍数を計算する関数を定義してみましょう。GCD 関数を使えば簡単です。TO LCM を実行します。
<![CDATA[
TO LCM :A :B
OP :A * :B / GCD :A :B
END
]]>
と定義します。* は掛け算を意味します。/ は割り算を意味します。* と / は同じ優先度ですから左から順に計算します。:A と :B を掛け、:A と :B の最大公約数で割ります。
関数の定義の仕方は一通りではありません。例えば、LCM は次のように定義しても良いです。
<![CDATA[
TO LCM :A :B
LOCAL :T
:T = :A
WHILE :T % :B != 0 [:T = :T + :A ]
OP :T
END
]]>
この関数の定義の意味は次の通りです。LOCAL :T という命令は :T というローカル変数を宣言しています。変数は数値を入れる入れ物で必ず : で始まり、英字で始まる英数字の名前を持ちます。ローカル変数とは宣言された手続きや関数の定義の中だけで有効な変数です。局所変数は LOCAL 変数名の並びで宣言します。変数名の並びとは変数名の列のことです。ローカル変数の宣言は必ず一行使って宣言して下さい。次の行の :T = :A は代入文です。:T の値として :A の値を割り当てよという命令です。:T の持っていた値は捨てられます。:A に割り当てられている値に変化はありません。これを普通 :T に :A を代入するといいます。次は WHILE 文です。
WHILE 文は
<![CDATA[
WHILE 条件式 [ 命令の列 ]
]]>
の形で使います。条件式が真の間、命令の列を実行します。命令の列を普通、命令の並びといいます。
<![CDATA[
:T % :B != 0
]]>
が条件式です。
元に戻って、WHILE :T % :B != 0 [:T = :T + :A ] は上の行で :T に :A の値を代入しているので、:T の値が :B の値で割り切れない間は :T = :T + :A を実行します。
:T = :T + :A は :T の値と :A の値の和を :T の新しい値にしなさいという代入文で :T の値が :A の値だけ増加します。従って、:A の倍数を次々 :T の値とし、:B で割り切れれば、この WHILE 文を終了します。この時、:T には :A と :B の最小公倍数が割り当てられているので、次の行で :T の値を LCNM :A :B の値としてこの関数の実行を終了すればいいのです。
このように、１行づつ分析して、それをまとめ上げて、全体として何をしているか考えるやり方をボトムアップと言います。他人の作ったプログラムを理解するための方法です。
これに対して、自分でプログラムを考えるときは、上の方から考えます。:A と :B の最小公倍数を求める。そのためには、:B の倍数になるまで、:A からはじめ、:A の２倍、:A の３倍、:A の４倍、・・・、としていくとよい。初めて :B の倍数になった :A の倍数が :A と :B の最小公倍数である。繰り返しなので、例えば、WHILE 命令を使うことにすると、:A の倍数を保持する変数として :T を使うことにし、まず、:T に :A を代入し（即ち、:T = :A）、:T が :B の倍数でない間は（即ち、:T % :B != 0）、:T に :A を加える（即ち、:T = :T + :A）。WHILE 命令が終わったときの :T が :A と :B の最小公倍数である。従って、
<![CDATA[
:T = :A
WHILE :T % :B != 0 [:T = :T + :A ]
OP :T
]]>
で:A と :B の最小公倍数が得られる。さらに、:T をこの関数だけで通用するように、局所変数にする（即ち、LOCAL :T）。このように考えて、
<![CDATA[
TO LCM :A :B
LOCAL :T
:T = :A
WHILE :T % :B != 0 [:T = :T + :A ]
OP :T
END
]]>
を導く方法をトップダウンと言います。トップダウンの方法は次のようです。まず何をしたいかを単純な文章にしてみる。それをするためには何をすればいいか、箇条書きしてみる。箇条書きしたそれぞれの文章を実現するためには何をすればいいか箇条書きしてみる。これを繰り返して、だんだん HUMMINGBIRD が理解できる命令の列に近づけていきます。他人の作ったプログラムを単に丸暗記する（多分、暗記できないと思いますが）のではなく、トップダウンでそのプログラムが導けるように練習していれば、アルゴリズムも理解できるようになり、自然にプログラムが作れるようになります。
ついでにもう一つのプログラムを示します。
<![CDATA[
TO LCM :A :B
LOCAL :I :T
FOR :I = 1 TO :B [:T = :I * :A IF :T % :B == 0 [BREAK]]
OP :T
END
]]>
でも最小公倍数を計算してくれます。二行目で :I と :T の二つのローカル変数を宣言しています。三行目は FOR 文です。
FOR 文は４通りの形式があります。
<![CDATA[
FOR 変数名 = 数式1 TO 数式2 [命令の並び]
]]>
の形式のときは、まず変数を数式1の値で初期化し、変数が数式2の値を超えるまで、命令の並びを実行するたびに、変数に 1 を加え、命令の並びを繰り返し実行します。与えた数式によっては、一回も命令の並びを実行しない場合もあります。
<![CDATA[
FOR 変数名 = 数式1 TO 数式2 STEP 数式3 [命令の並び]
]]>
の形式のときは、まず変数を数式1の値で初期化し、変数が数式2の値を超えるまで、命令の並びを実行するたびに、変数に数式3の値を加え、命令の並びを繰り返し実行します。与えた数式によっては、一回も命令の並びを実行しない場合もあります。
<![CDATA[
FOR 変数名 = 数式1 DOWNTO 数式2 [命令の並び]
]]>
の形式のときは、まず変数を数式1の値で初期化し、変数が数式2の値を下回るまで、命令の並びを実行するたびに、変数から 1 を減じ、命令の並びを繰り返し実行します。与えた数式によっては、一回も命令の並びを実行しない場合もあります。
<![CDATA[
FOR 変数名 = 数式1 DOWNTO 数式2 STEP 数式3 [命令の並び]
]]>
の形式のときは、まず変数を数式1の値で初期化し、変数が数式2の値を下回るまで、命令の並びを実行するたびに、変数から数式3を減じ、命令の並びを繰り返し実行します。与えた数式によっては、一回も命令の並びを実行しない場合もあります。
今回は STEP 数式の部分がありません。このような時は :I の増分は 1 です。:I を 1 から初めて :B まで [ と ] の間の命令を実行します。:T = :I * :A は代入文で :I と :A の積を :T に代入します。次の命令は IF 文です。
:T % :B == 0 が条件式で :T が :B で割り切れるなら BREAK が実行されます。
BREAK 命令は
<![CDATA[
BREAK
]]>
の形式で使い、FOR 文や WHILE 文や REPEAT 文や DO UNTIL 文のループの実行を終了する命令です。
従って、BREAK を実行すると一番内側のループを抜けます。今の場合、:A を 1 倍、2 倍、3倍としていって、:B の倍数になれば、FOR 文の実行を終了します。この時、:T には :A と :B の最小公倍数が割り当てられているはずですから、次の行で :T をこの関数の値とします。最初のうちは、思いつく方法でプログラムを作れば良いです。
最大公約数を計算する考え方の単純なプログラムとして次のような定義も出来ます。
<![CDATA[
TO GCD :A :B
LOCAL :T :I
FOR :I=1 TO :A [IF (:A % :I == 0) && (:B % :I == 0) [:T = :I]]
OP :T
END
]]>
ローカル変数 :I を 1 から :A まで変化させ、:I が :A と :B の両方を割りりるとき、即ち公約数のとき、:I の値を :T に保存しています。従って、FOR 文を終えたとき、:T には :A と :B の最大公約数がセットされています。さらに、上のプログラムではローカル変数 :T と :I を使った行儀の良いプログラムにしていますがグローバル変数を使って次のように定義しても良いです。
<![CDATA[
TO GCD :A :B
FOR :I=1 TO :A [IF (:A % :I == 0) && (:B % :I == 0) [:T = :I]]
OP :T
END
]]>
グローバル変数は宣言しなくても使えて便利ですが、深くネストした手続きで変更されたのが全体に及びますから、便利ですが、注意が必要です。GCD は次の様に定義すればもっと効率が良くなります。
<![CDATA[
TO GCD :A :B
LOCAL :I ;L
IF :A < :B [:L = :A][:L = :B]
FOR :I=:L DOWNTO 1 [IF (:A % :I == 0) && (:B % :I == 0) [BREAK]]
OP :I
END
]]>
:A と :B の小さいほうを :L に代入します。:I を :L から 1 まで順に小さくしていって、最初に :I が :A と :B の両方を割り切るとき :I の値が :A と :B の最大公約数ですから、BREAK 命令で FOR 文を終わります。:I を GCD :A :B の値として関数を終了します。基本的には人間が考える通りプログラムすればいいです。小学生でも実行できるぐらい細かく手順を分解できれば、大抵プログラミングできます。ただ数学と違う面もあります。例えば、:A と :B を素因数分解して、最大公約数や最小公倍数を求めるという方法は勿論可能ですがプログラム化するのは大変です。初心者の時は小さいプログラムをたくさん作ってください。実行速度が気になりだしたら、アルゴリズムの本で勉強してください。HUMMINGBIRD では大きなプログラムは作りませんから、どんなプログラムを作ってもたいした差はないですが、HUMMINGBIRD を卒業し、Java や C++ のコンパイラなどで、本格的なオブジェクト指向プログラミングに挑戦するようになると、アルゴリズムの勉強が重要になります。データ構造の勉強も必要です。本格的なプログラムでは素人の作ったプログラムとプロの作ったプログラムでは実行速度に数千倍、数万倍以上の差が出るのは日常茶飯事です。参考書は Niklaus Wirth 著「アルゴリズム＋データ構造＝プログラム」日本コンピュータ協会がお勧めです。HUMMINGBIRD にはデータ構造と呼べるものは何もありません。データは基本的には倍精度の実数だけです。
もとに戻って、POLY を停止するように修正しましょう。:ANGLE の値から繰り返しの回数をまず計算します。:ANGLE と 360 の最小公倍数を :ANGLE で割ったものが繰り返しの回数です。
<![CDATA[
TO POLY :SIZE :ANGLE
LOCAL :T
:T = (LCM :ANGLE 360) / :ANGLE
REPEAT :T [FD :SIZE RT :ANGLE]
END
]]>
この様に POLY を定義すれば、例えば POLY 100 144 と実行すれば、星型正五角形を描いて停止するはずです。
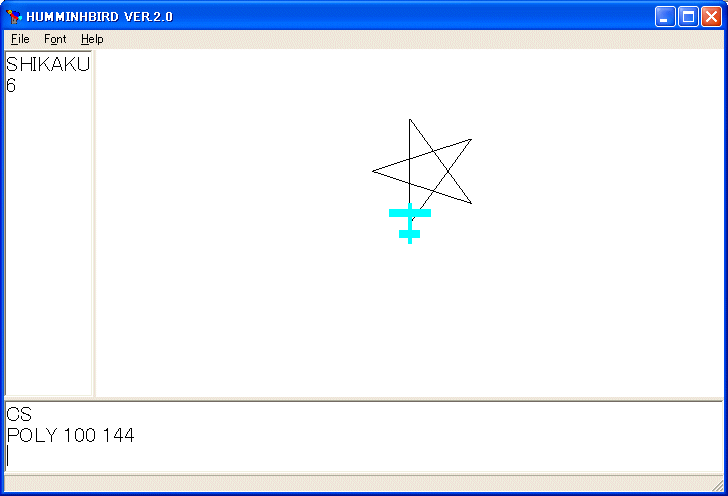
次の様に定義しても良いです。回転角の合計を保存していて、360 の倍数になれば停止します。
<![CDATA[
TO POLY :SIZE :ANGLE
LOCAL :T
:T = 0
DO [
FD :SIZE RT :ANGLE
:T := :T + :ANGLE
] UNTIL :T % 360 == 0
END
]]>
DO UNTIL 文は
<![CDATA[
DO [ 命令の列 ] UNTIL 条件式
]]>
の形をしていて、まず命令の列を実行し、条件式を調べます。条件式が偽の間は命令の列を繰り返し実行します。WHILE 文は条件が偽であれば一回も命令の列を実行しませんが、DO UNTIL 文は条件が真でも一回は命令の列を実行します。引数を増やして、回転角の合計を再帰呼び出しの引数として渡すことも出来ます。
<![CDATA[
TO POLY :SIZE :ANGLE :JUNK
FD :SIZE RT :ANGLE
:JUNK = :JUNK + :ANGLE
IF :JUNK % 360 == 0 [STOP]
POLY :SIZE :ANGLE :JUNK
END
]]>
でもいいです。POLY 100 144 0 のように使います。
STOP 命令は
<![CDATA[
STOP
]]>
の形式で使い、手続きの実行を終了します。
HUMMINGBIRD には円を描く命令はありません。適当な正多角形で代用します。正 360 角形なら十分です。
<![CDATA[
REPEAT 360 [FD 1 RT 1]
]]>
を実行すると次のような円に見える正 360 角形を描きます。
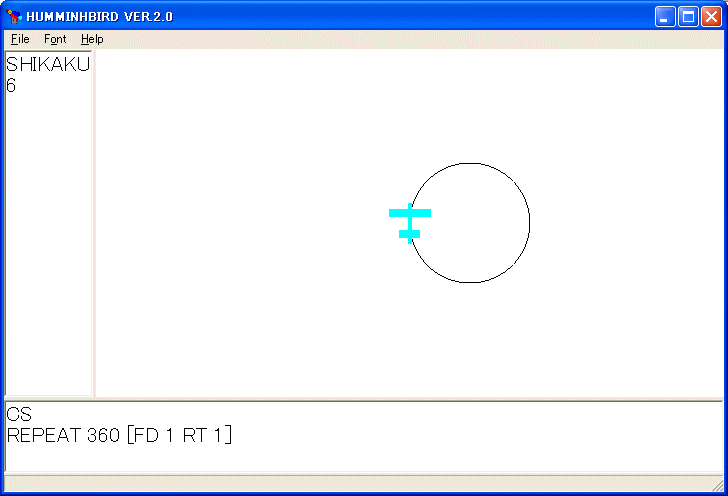
円の大きさを決めるには前進する大きさを決めればいいですが、小学校で習った「円周の長さ = 2 × 半径の長さ × 円周率」を使えば、半径の長さを指定して、円を描くことができます。
<![CDATA[
TO CYCLE :R
LOCAL :X
:X = :R * PI / 180
REPEAT 360 [FD :X RT 1]
END
]]>
で半径 :R の円を描く手続きを定義できます。実際は、少し誤差が出ますが、実用上は問題ない大きさです。
<![CDATA[
LOCAL :X
]]>
の行は局所変数の宣言です。局所変数はその手続きだけで通用する変数で、大域変数に同じ名前の変数があっても局所線数の方が優先されます。大域変数は宣言しなくても（宣言しなければ大域変数ですが）使えるし便利ですが、発見しにくいバグを発生する可能性があるのでこのように手続きの中だけで使う変数は局所線数にする方がいいです。変数 :X には一歩の歩幅を計算してセットしています。局所変数の宣言は局所変数を使う前ならどこでも宣言できます。ただし、局所変数の宣言は
<![CDATA[
LOCAL :X :Y :Z
]]>
のように一度に複数宣言してもいいですが、その行にはその他の命令は書かないで下さい。手続きの引数の宣言のときと同じ理由で HUMMINGBIRD 自身のプログラミングが楽なのでそのような仕様にしています。C のような他の言語と異なり、宣言と初期化を同時にすることはできません。CYCLE の手続きを HUMMINGBIRD に覚えさせ
<![CDATA[
FOR :X=20 TO 120 STEP 20 [CYCLE :X]
]]>
を実行すると次のような図を描きます。
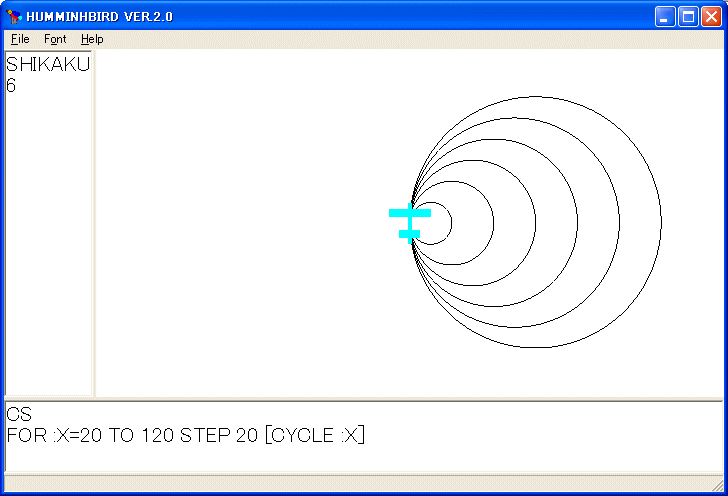
飛行機の位置を中心として半径 :R の円を描く手続きは次のようになります。
<![CDATA[
TO CYCLE2 :R
LOCAL :X
:X = :R * PI / 180
PU FD :R RT 90 PD
REPEAT 360 [FD :X RT 1]
PU LT 90 BK :R PD
END
]]>
<![CDATA[
REPEAT 5 [PU FD 80 PD CYCLE2 40 RT 72]
]]>
を実行すると次のような図を描きます。
手続き CYCLE2 は次のように定義してもいいです。
<![CDATA[
TO CYCLE2 :R
LOCAL :X
:X = :R * PI / 180
PUSH PU FD :R RT 90 PD
REPEAT 360 [FD :X RT 1]
PU POP PD
END
]]>
PUSH と POP という命令を使っています。
PUSH は
<![CDATA[
PUSH
]]>
の形式で使い、「スタック」といわれる飛行機の状態（位置と向き）を保存する記憶領域の一番上に、現在の飛行機の状態を保存します。
POP は
<![CDATA[
POP
]]>
の形式で使い、「スタック」の一番上から保存しておいた飛行機の状態（位置と向き）を取り出し、保存しておいた飛行機の状態に、現在の飛行機の状態を変化させます。このとき位置の移動があり、もしペンが下がっていれば、線を描きます。POP で取り出すのは、「スタック」の一番上の飛行機の状態（一番最後に、保存したもの）ですので間違わないようにして下さい。
ペンが下がっていれば、線を描くので、PU POP PD と POP 命令の前後でペンの上げ下げをしています。「スタック」というのは、 PUSH を繰り返すと次々に飛行機の状態が保存されますが、 POP 命令を実行されたとき復元される飛行機の状態は一番最後に保存された飛行機の状態です。POP 命令を実行するたびに保存してあった飛行機の状態はなくなっていきます。トータルとして PUSH の個数と POP の個数は一致しなければなりません。複雑な行動をした後、元の位置に飛行機を戻すために非常に強力なテクニックです。
半径 :R で中心角が :ANGLE の扇形を描く手続きは
<![CDATA[
TO ARC :R :ANGLE
LOCAL :X
:X = :R * PI / 180
RT :ANGLE/2 FD :R LT 90
REPEAT :ANGLE [FD :X LT 1]
LT 90 FD :R LT 180-:ANGLE/2
END
]]>
で与えられます。
<![CDATA[
ARC 120 300
]]>
を実行すると次のような図を描きます。
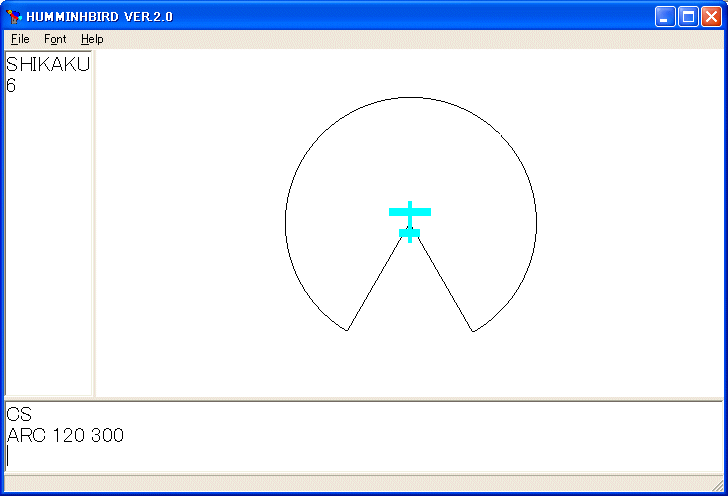
葉っぱのような図形を描くには、外角の和は 360 度に注意すれば
<![CDATA[
TO LEAF :R :ANGLE
LOCAL :X :Y
:X = :R * PI / 180
:Y = :R * SIN :ANGLE/2
PU FD :Y PD RT 180-:ANGLE/2
REPEAT :ANGLE [FD :X RT 1]
RT 180-:ANGLE
REPEAT :ANGLE [FD :X RT 1]
LT :ANGLE/2 PU BK :Y PD
END
]]>
という手続きを使えばいいです。
<![CDATA[
LEAF 120 120
]]>
を実行すると次のような図を描きます。
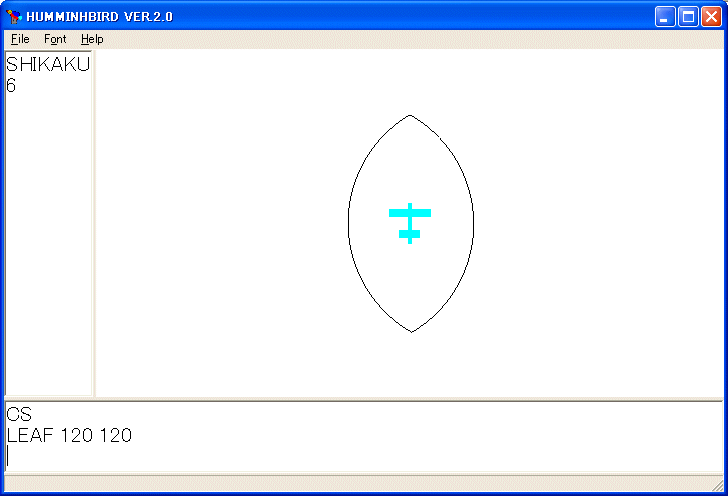
重心から葉っぱの縁までの長さを計算するには三角関数の定義を知っている必要があります。正弦関数は
<![CDATA[
SIN 式
]]>
の形式で使えます。余弦関数は
<![CDATA[
COS 式
]]>
の形式で、正接関数は
<![CDATA[
TAN 式
]]>
の形式で使えます。式の値は度で評価します。ラジアンで評価できるようにするには
<![CDATA[
RADIANMODE
]]>
を実行すれば、三角関数と逆三角関数（頭に A を付けます）がラジアンで評価されるようになります。
<![CDATA[
DEGREEMODE
]]>
を実行すれば、三角関数と逆三角関数が度で評価されるようになります。初期設定（デフォルト）は度です。
円に内接する正 :N 角形や星形正 :N 角形を描くには、三角関数を使えばいいですが、次のように考えることもできます。円を描くとき、正 :N 角形の頂点の位置を HUMMINGBIRD に覚えさせておき、それらを結んで正 :N 角形や星形正 :N 角形を描けばいいです。この考えをプログラミングすればいいです。
まず円に内接する正 :N 角形を描く手続きは次のようになります。
<![CDATA[
TO INSCRIBEDPOLY :SIZE :N
LOCAL :X :I
:X = :SIZE * PI / 180
:I = 0
PUSH PU FD :SIZE PD RT 90
REPEAT :N [PUT 1 :I :I = :I+1 REPEAT 360/:N [FD :X RT 1]]
:I = 0
PU GET 1 :I :I = :I + 1 PD
REPEAT :N [GET 1 :I :I = (:I + 1) % :N]
PU POP PD
END
]]>
でいいです。
<![CDATA[
INSCRIBEDPOLY 120 7
]]>
を実行すると次のように円に内接する正七角形を描きます。
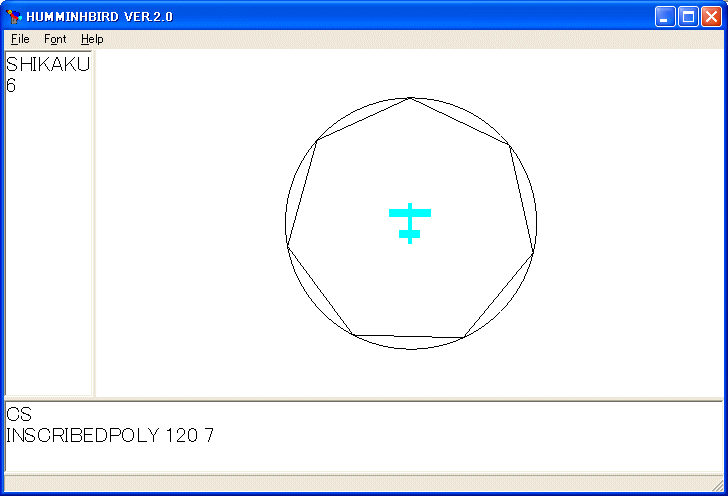
PUT と GET 命令を使っています。PUT 命令は
<![CDATA[
PUT 式1 式2
]]>
の形式で使い、式1 の値は 1 か 2 で、 1 は一番目の配列を指示し、 2 は二番目の配列を指示し、飛行機の状態（位置と向き）を配列の式2 の値で指示される位置に保存します。GET 命令は
<![CDATA[
GET 式1 式2
]]>
の形式で使い、式1 の値は 1 か 2 で、 1 は一番目の配列を指示し、 2 は二番目の配列を指示し、飛行機に配列の式2 の値で指示される位置から保存されているタートルの状態（位置と向き）を復元します。PUT 命令で円周上の正 :N 角形の頂点の位置を保存し、GET 命令を使って保存した円周上の正 :N 角形の頂点の位置を順番に復元することにより、正 :N 角形を描いています。
後で説明するように、HUMMINGBIRD は飛行機とヘリコプターと二つのタートルを持っています。ヘリコプターの状態を保存したり、復元したりするには、PUT と GET 命令を
PUT2 と GET2 と 2 を付けた命令で表現します。
<![CDATA[
:I = (:I + 1) % :N
]]>
は変数 :I を一つづつ増やしていますが変数 :I が :N なったとき :N ではなく 0 にするために :N で割った剰余を変数 :I に代入するために二項演算子 % を使って、 :I + 1 を :N で割った剰余を変数 :I に代入しています 。
円に内接する星形正 :N 角形を描くには、保存している頂点を飛ばして結べばいいので
<![CDATA[
TO INSCRIBEDSTARPOLY :SIZE :N :M
LOCAL :X :I
:X = :SIZE * PI / 180
:I = 0
PUSH PU FD :SIZE PD RT 90
REPEAT :N [PUT 1 :I :I = :I+1 REPEAT 360/:N [FD :X RT 1]]
:I = 0
PU GET 1 :I :I = :I + :M PD
REPEAT :N [GET 1 :I :I = (:I + :M) % :N]
PU POP PD
END
]]>
でいいです。
<![CDATA[
INSCRIBEDSTARPOLY 120 9 2
]]>
を実行すると次のように円に内接する星形正九角形を描きます。
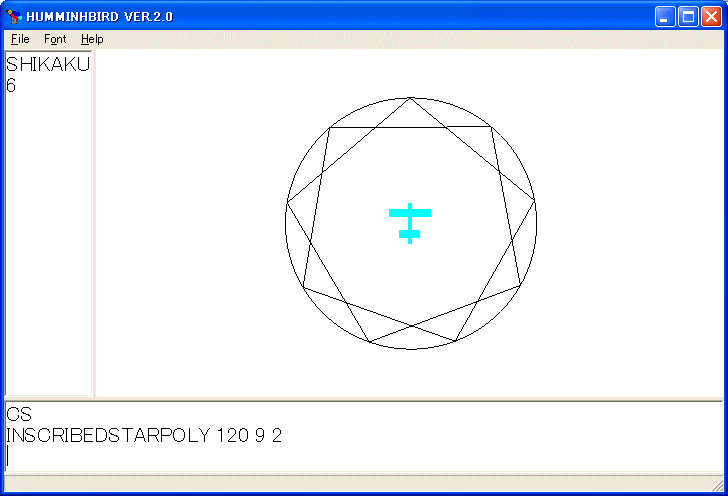
今まで述べたことを使えば次のようなパラソルを描く手続きが理解できるようになっていると思います。
<![CDATA[
TO PARASOL :SIZE
LOCAL :X
:X = :SIZE / 3 * PI / 180
PUSH FD :SIZE/3
LT 90
REPEAT 90 [ FD :X LT 1]
LT 180
REPEAT 180 [ FD :X LT 1]
RT 180
REPEAT 90 [ FD 3 * :X RT 1]
LT 90 FD :SIZE/3 BK :SIZE/3 RT 90
REPEAT 90 [ FD 3 * :X RT 1]
LT 180
REPEAT 180 [ FD :X LT 1]
LT 180
REPEAT 90 [ FD :X LT 1]
RT 90
BK 4 * :SIZE / 3
REPEAT 180 [BK :X / 2 LT 1]
PU POP PD
END
]]>
<![CDATA[
PARASOL 120
]]>
を実行すると次のような図を描きます。
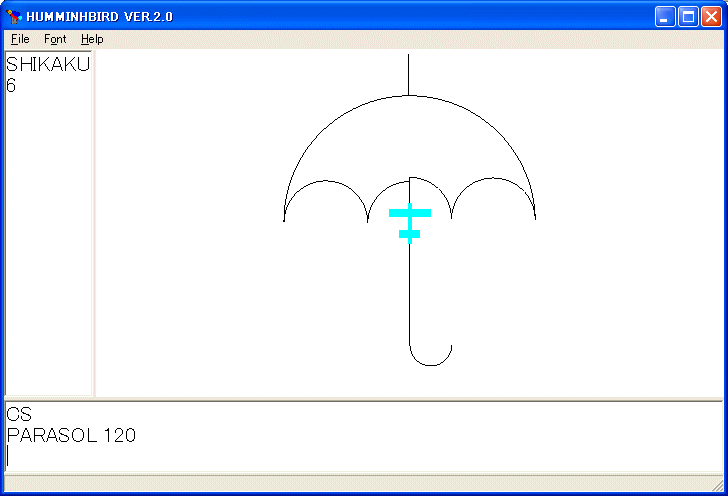
少し誤差が出ているのが目につきます。これで色々面白い線画が描けるようになったはずです。
線画だけでは面白くありませんから、面を塗りつぶしてみます。POLYMODE と NONPOLYMODE を使います。凸多角形を描く命令を POLYMODE と NONPOLYMODE で囲うと現在の色で塗りつぶされた凸多角形を描きます。
上で定義した POLY を修正して
<![CDATA[
TO FILLPOLY :SIZE :N
POLYMODE
REPEAT :N [FD :SIZE RT 360/:N]
NONPOLYMODE
END
]]>
と定義します。
<![CDATA[
FILLPOLY 100 5
]]>
を実行すると黒く塗りつぶされたせい正五角形を描きます。これはデフォルトの色が黒だからです。色を変えたければ、FILLPOLY 100 5 の前で SETCOLOR を使って色を指定しておきます。
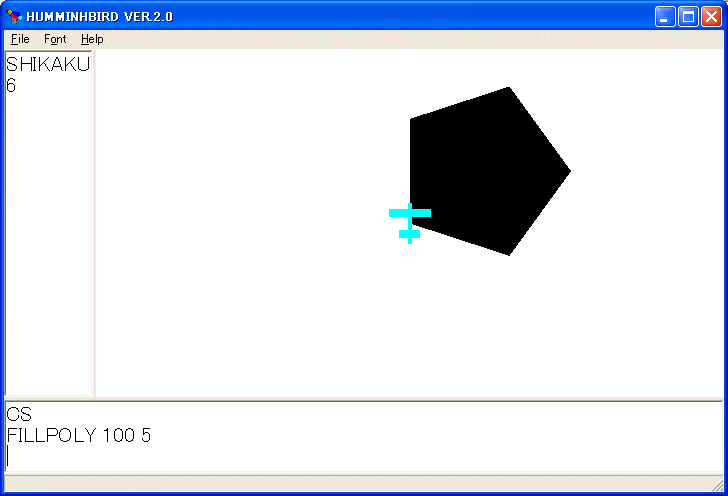
正確に言うと描く凸多角形を反時計回りに描くか時計回りに描くかで面が表向きか裏向きかの違いがあります。光があったっているとき違いが出ます。平面図形ですから、
<![CDATA[
DISABLELIGHTING
]]>
で光を消して、光の影響を受けないようにすれば、描く向きを考えなくてもいいです。これがデフォルトです。
星形正多角形は凸ではありませんから、 POLYMODE と NONPOLYMODE で囲ってもうまくいきません。一つの方法は星形正多角形を凸多角形に分割してそれぞれを塗りつぶすことです。これを簡単に実行するために HUMMINGBIRD にはうまい方法が準備されています。HUMMINGBIRD には飛行機の他にもう一つのタートルであるヘリコプターがあります。ヘリコプターは初期状態では隠れています。見えるようにするには ST2 を実行します。例外もありますが基本的に飛行機に対する命令に 2 を点ければヘリコプターに対する命令になります。
<![CDATA[
CS
HT ST2
]]>
を実行すると
ヘリコプターが現れます。タートルが二つ準備されているのは、二つのタートルを協調させて図形を描くためです。SYNCHRO と NONSYNCHRO で囲うと、飛行機とヘリコプターのペンが共に下がっていれば、ヘリコプターが移動したとき、飛行機の位置と移動した後のヘリコプターの位置を結ぶ線分を描きます。飛行機が移動しても何も描きません。飛行機とヘリコプターで対称ではありませんが、この方が便利だと考えたからです。この機能は正多面体や正多角柱や正多角反柱を描くとき使うと便利です。SYNCHRO SURFMODE と NONSYNCHRO NONSURFMODE で囲うと、飛行機とヘリコプターのペンが共に下がっていれば、タートル（飛行機またはヘリコプター）が移動すれば、移動したタートルと移動しないタートルでできる三角形（移動したタートルの元の位置と移動したタートルの現在の位置と移動しないタートルの現在の位置の三点でできる三角形）を現在の色で塗りつぶします。この場合は、飛行機が移動したときは、移動の向きに進んだときに反時計回りに三角形を描くなら、三角形は表向きで、ヘリコプターが移動したときは、移動の向きに進んだときに時計回りに三角形を描くなら、三角形は表向きになります。向きが重要になるのは双曲空間で三次元の図形を描いたときやユークリッド空間で複雑な図形を描いたとき、色々な光を当てることできれいな図形を描きたいときに問題になります。この場合も平面図形を描いているときは
<![CDATA[
DISABLELIGHTING
]]>
で光を消して、光の影響を受けないようにすれば、描く向きを考えなくてもいいです。この状態がデフォルトです。
次のような手続きを考えます。
<![CDATA[
TO POLY2 :SIZE :N
LOCAL :A
:A = 2 * :SIZE * SIN 180 / :N
PUSH PU FD :SIZE RT 90 + 180 / :N PD
REPEAT :N [FD :A RT 360/:N]
PU POP PD
END
]]>
<![CDATA[
POLY2 100 5 POLY2 100 10
]]>
を実行すると次のような図形を描きます。
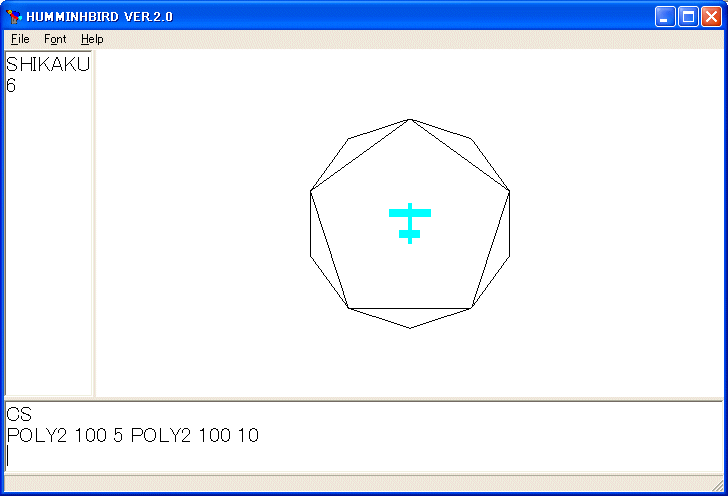
この手続きでは引数として、正 :N 角形の :N と正 :N 角形の重心と頂点との間の距離 :SIZE （順序は逆ですが）を与えて正 :N 角形を描きます。
これを SYNCHRO SURFMODE と NONSYNCHRO NONSURFMODE で囲って次のように修正します。
<![CDATA[
TO FILLPOLY2 :SIZE :N
LOCAL :A
:A = 2 * :SIZE * SIN 180 / :N
PUSH PU FD :SIZE RT 90 + 180 / :N PD
SYNCHRO SURFMODE
REPEAT :N [SETCOLOR RAND RAND RAND FD :A RT 360/:N]
NONSYNCHRO NONSURFMODE
PU POP PD
END
]]>
<![CDATA[
FILLPOLY2 120 10
]]>
を実行すると次のような図形を描きます。
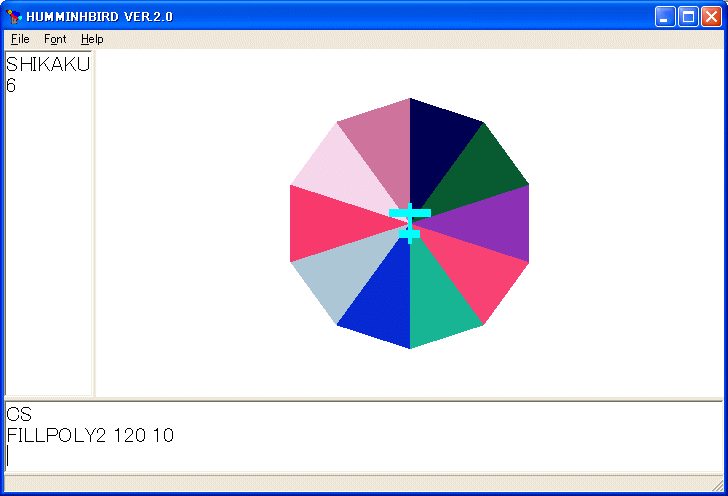
RAND は 0 と 1 の間の乱数を与える引数なしの組み込み関数です。この手続きは表面上ヘリコプターに対する命令は現れていませんが、ヘリコプターが中心にいることが前提になっています。
<![CDATA[
PU FD 50 PD FILLPOLY2 100 10
]]>
を実行すると次のような図形を描きます。
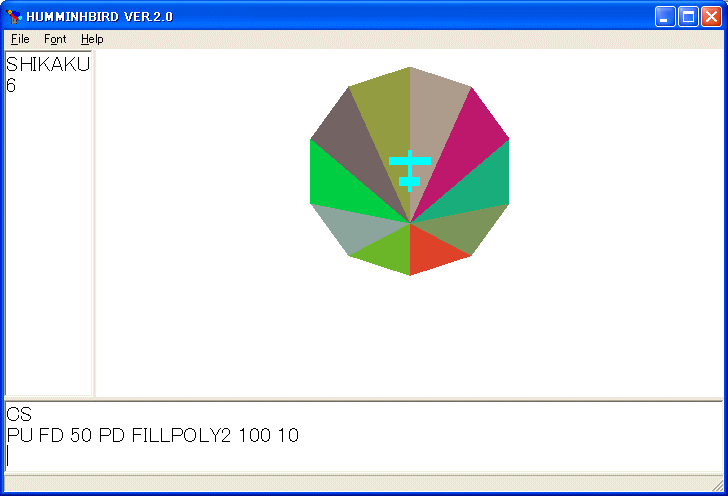
さてこのことをふまえて、塗りつぶされた星形正多角形を描く手続きを作ってみましょう。
次のような手続きを考えます。
<![CDATA[
TO STARPOLY2 :SIZE :N :M
LOCAL :S :A
:S = 2 * :SIZE * SIN 180 * :M / :N
:A = 360 * :M / :N
PUSH PU FD :SIZE RT 90 + 180 * :M / :N PD
REPEAT :N [FD :S RT :A]
PU POP PD
END
]]>
<![CDATA[
STARPOLY2 130 7 3
]]>
を実行すると次のような図形を描きます。
この手続きの考え方は POLY2 と基本的に同じです。これを修正して次のようにします。
<![CDATA[
TO FILLSTARPOLY2 :SIZE :N :M
LOCAL :S :A
:S = 2 * :SIZE * SIN 180 * :M / :N
:A = 360 * :M / :N
PUSH2 PUSH PUSH TF PU2 POP2 PD2
PU FD :SIZE RT 90 + 180 * :M / :N PD
SYNCHRO SURFMODE
REPEAT :N [FD :S RT :A]
NONSYNCHRO NONSURFMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
FILLSTARPOLY2 130 7 3
]]>
を実行すると次のような図形を描きます。
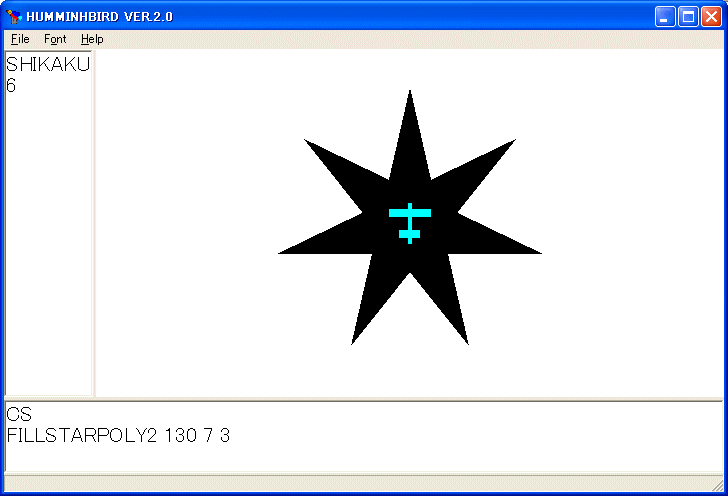
PUSH2 と POP2 はヘリコプターの状態を保存するためのスタックに対する保存と復元の命令です。TF は TRANSFER の省略形で飛行機のためのスタックからヘリコプターのためのスタックへタートルの状態を転送するための命令です。飛行機のスタックからは飛行機の状態が一つ無くなります。逆の命令は TF2 で TRANSFER2 の省略形です。ごちゃごちゃやっているみたいですが、ヘリコプターの状態をスタックに保存し、飛行機の状態を二度スタックに保存し、その一つをヘリコプターのスタックに転送し、ヘリコプターに復元し、飛行機とヘリコプターの状態を同じにします。飛行機を使って星形正多角形を描き、最後に飛行機とヘリコプターを元の状態に戻しています。
このように手続きを作っておけば
<![CDATA[
PU LT 90 FD 150 RT 90 PD FILLSTARPOLY2 130 7 3
]]>
を実行しても次のように正しい星形正多角形を描きます。
更に次のように定義します。
<![CDATA[
TO ZU :SIZE :N :M
LOCAL :A :B
:A=500/:SIZE/2 :B=250/:SIZE/2
FOR :I=-:A/2 TO :A/2 [
FOR :K=-:B/2 TO :B/2 [
PU SETPOS :I*:SIZE*2 :K*:SIZE*2 0 PD
FILLSTARPOLY2 :SIZE :N :M
]
]
END
]]>
<![CDATA[
ZU 40 5 2
]]>
を実行すると次のような図を描きます。。
HUMMINGBIRD は三次元 LOGO です。タートルは三次元空間を動くことが出来ます。左右に向きを変えるだけでなく、上下に向きを変えたり、右肩下がりや左肩下がりに状態を変化することが出来ます。これらの命令はヘルプの手続きのマニュアルを読んでください。これにより前進だけで自由に空間を移動できます。例えば、
<![CDATA[
REPEAT 360 [FD 10 RT 10 UP 20]
]]>
を実行すれば、常螺旋を描きます。
常螺旋であることを実感したければ、マウスで画面をドラッグしてみて下さい。
立方体を描くには次のようにします。
<![CDATA[
TO cube :x
repeat 4 [fd :x down 90 fd :x bk :x up 90 rt 90]
down 90 fd :x up 90
repeat 4 [fd :x rt 90]
down 90 bk :x up 90
end
]]>
と定義すれば、cube 100 のように使う立方体を描く手続きを定義できます。
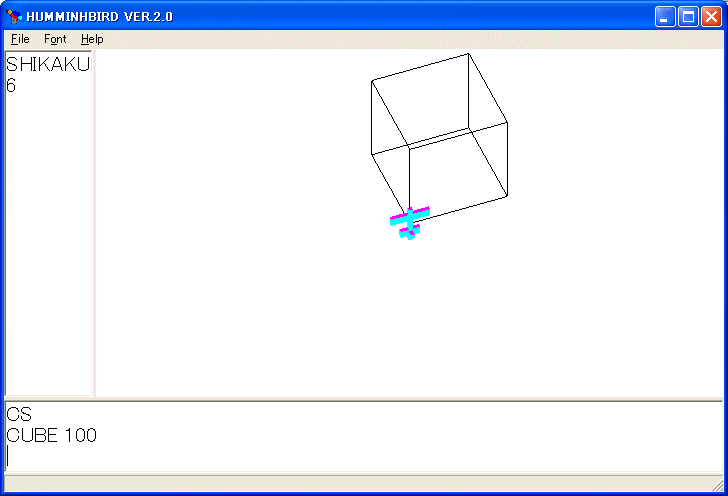
この図は立方体を描いたことが分かるようにマウスで回転しています。down 90 は頭を 90 度下げよという命令で、up 90 は頭を 90 度上げよという命令です。
DOWN 命令は
<![CDATA[
DOWN 式
]]>
の形式で使い、式の値だけ飛行機が頭を下に下げます。逆の動作は UP 命令を使います。UP 命令は
<![CDATA[
UP 式
]]>
の形式で使い、式の値だけ飛行機が頭を上に上げます。
立方体は分かりやすいですね。直方体を描く手続きも同様にできます。自分で考えてください。
このプログラムを次のように修正します。
<![CDATA[
TO CUBE2 :X
REPEAT 4 [
FD :X SPHERE :X/8 DOWN 90 FD :X SPHERE :X/8
BK :X UP 90 RT 90
]
DOWN 90 FD :X UP 90
REPEAT 4 [FD :X RT 90]
DOWN 90 BK :X UP 90
END
]]>
<![CDATA[
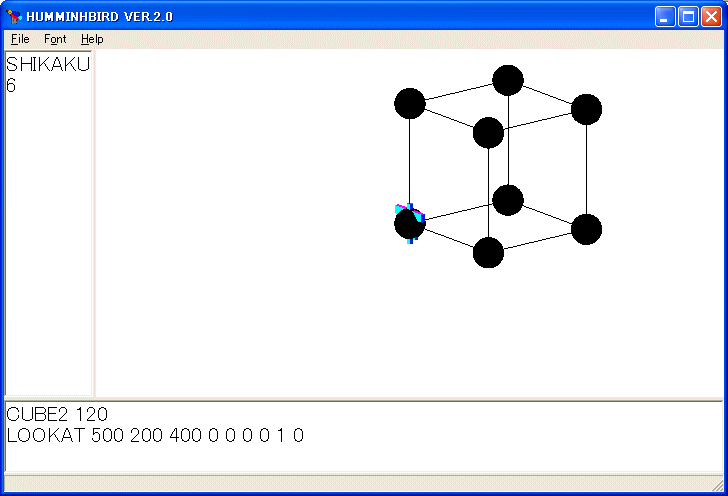
CUBE2 120
LOOKAT 500 200 400 0 0 0 0 1 0
]]>
を実行しました。SPHERE 命令は
<![CDATA[
SPHERE 式
]]>
の形式で使い、飛行機の位置を中心とし、半径が式の値である球を現在の色で描きます。SPHERE2 命令は中心がヘリコプターの位置になります。
立方体や直方体は小学生での理解できると思いますが、その他の図形はとたんに難しくなります。タートルグラフィックスに拘ると、正四面体を描くためには、解析幾何学でもだめで、球面幾何学の知識が必要になります。
<![CDATA[
TO TETRA :S
REPEAT 3 [FD :S RT 120]
YAW 180 - ACOS 1/3
REPEAT 3 [FD :S LT 120]
LT 60 YAW 180 - ACOS 1/3
REPEAT 3 [FD :S LT 120]
YAW -180 + ACOS 1/3 RT 60 YAW -180 + ACOS 1/3
END
]]>
と定義すれば、TETRA 150 のように使う正四面体を描く手続きを定義できます。
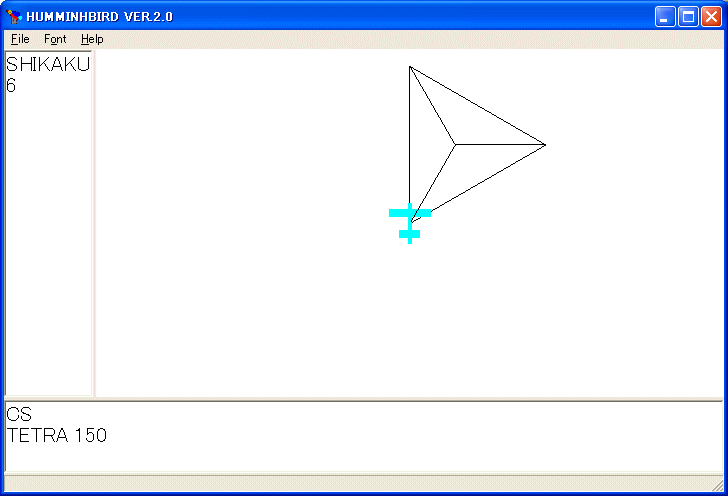
球面幾何学で習う余弦法則を使えば良いです。三角形 ABC は球面三角形で、辺 a は頂点 A に、辺 b は頂点 B に、辺 c は頂点 C に対するものとする。辺の余弦法則：cos a = cos b cos c + sin b sin b cos A と角の余弦法則：cos A = - cos B cos C + sin B sin C cos a というやつです。辺の余弦法則を使って、正四面体の面の間の角が arccos 1/3 であることが分かります。YAW 数値 が体を傾ける命令です。
。YAW 命令は
<![CDATA[
YAW 式
]]>
の形式で使い、式の値だけ飛行機が右肩を下に下げます。ACOS は
<![CDATA[
ACOS 式
]]>
の形式で使い、式の値の逆余弦関数の値を与える組み込み関数です。上のプログラムでは正四面体の二面角（二つの面のなす角）が ACOS 1/3 で与えられるという事実を使っています。
正四面体を描く別の方法を考えて見ます。
まず正四面体の枠組みの二つの線のなす角は
<![CDATA[
arccos(-1/3)
]]>
であることが分かります。
したがって、正四面体の枠組みは次のプログラムで描けます。ここで :A は枠組みの線の長さです。
<![CDATA[
TO TETRAFRAME :A
LOCAL :THETA
:THETA = ACOS -1/3
FD :A BK :A
DOWN :THETA
FD :A BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A BK :A
UP :THETA
END
]]>
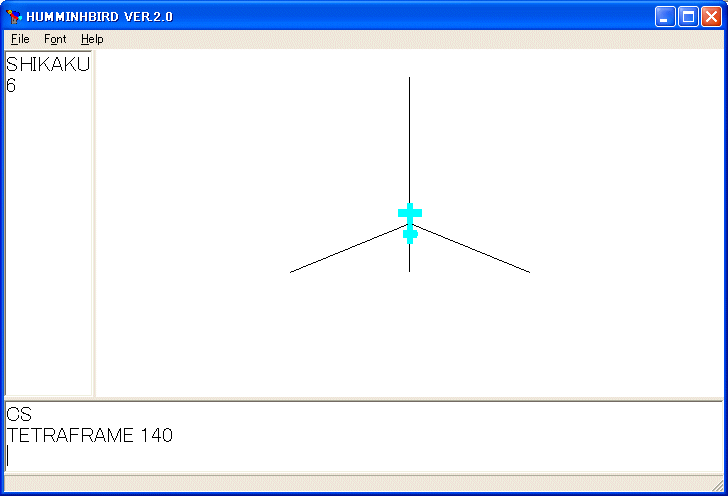
TETRAFRAME 140 を実行しました。このプログラムで定まる頂点の位置を覚えておき、それらを結んで稜線や面を描けば良いです。線画の正四面体を描くプログラムは次のようになります。枠組みは消しています。
<![CDATA[
TO TETRA :A
LOCAL :THETA
:THETA = ACOS -1/3
PU FD :A PUT 1 0 BK :A
DOWN :THETA
FD :A PUT 1 1 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 2 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 3 BK :A
UP :THETA
PUSH PUSH2
GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO
GET2 1 2 GET2 1 3 GET2 1 1
NONSYNCHRO
GET2 1 2 GET2 1 3 GET2 1 1
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
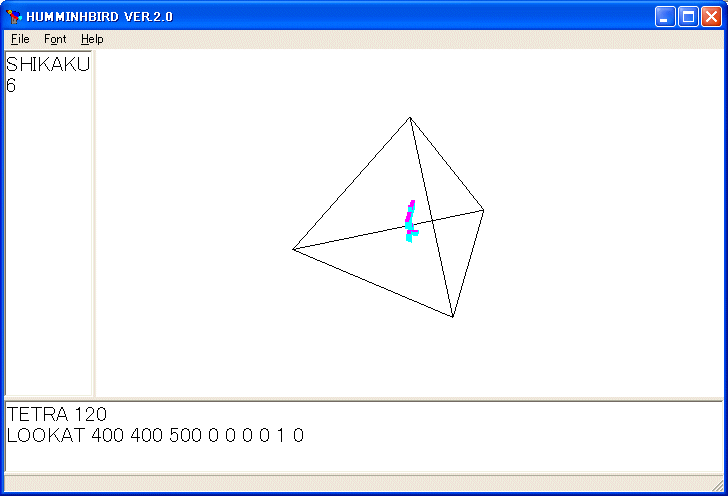
TETRA 120
LOOKAT 400 400 500 0 0 0 0 1 0
]]>
を実行しました。マウスで回転する代わりに、LOOKAT 命令でカメラの位置を指示しています。
LOOKAT 命令はカメラを移動さす命令で
<![CDATA[
LOOKAT 式1 式2 式3 式4 式5 式6 式7 式8 式9
]]>
の形式で使い、カメラを座標（式1 の値、式2 の値、式3 の値）の位置に移動させ、カメラの向きの中心を座標（式4 の値、式5 の値、式6 の値）の点として狙い、カメラの上向きの方向ベクトルを（式7 の値、式8 の値、式9 の値）とせよという命令です。
つまり LOOKAT 命令は引数を９個取り、最初の３個でカメラの位置を指示し、次の３個でカメラが見ている中心点を指示し、最後の３個でカメラの向きを指定するベクトルを指定します。
面を描くプログラムは次のようになります。
<![CDATA[
TO TETRAFILL :A
LOCAL :THETA
:THETA = ACOS -1/3
FD :A PUT 1 0 BK :A
DOWN :THETA
FD :A PUT 1 1 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 2 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 3 BK :A
UP :THETA
PUSH PUSH2
PU GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET2 1 1
NONSYNCHRO NONSURFMODE
SETCOLOR RAND RAND RAND
POLYMODE
GET2 1 2 GET2 1 3 GET2 1 1
NONPOLYMODE
PU POP PD PU2 POP2 PD2
END
]]>
TETRAFILL 140 を実行すると次の図が描かれます。
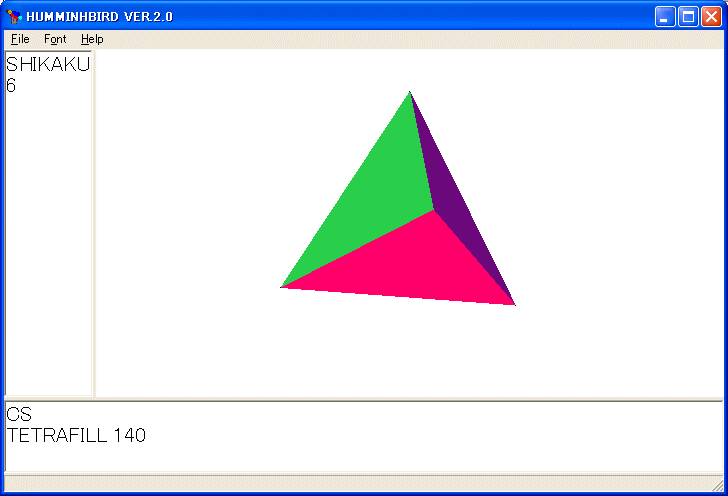
マウスで画面を回転しています。
これらのプログラムは後で説明する双曲空間でもそのまま通用します。
他の正多面体を描くにはどのように定義すればいいのでしょうか？考えてみて下さい。結構面倒くさいです。挑戦してみてください。KITE や KITE3 のサンプルプログラムに一つの解答を与えています。HUMMINGBIRD は座標を使って三次元の図形を描く機能もサポートしましたが、HUMMINGBIRD ではそのようにして描いた図形は柔軟性がありませんから（回転したり平行移動したりして、他のプログラムの部品として使うことがタートルグラフィックスのように自由にはならない）ので、タートルグラフィックスに拘っています。それで、三次元の機能の大部分は大学生しか使いこなせないものになってしまいました。
上で説明したように Synchro という命令を導入しました。Synchro 命令を実行した時には、シンクロ状態になり、二匹目のタートルが移動した時、両方のタートルが PD ならば二匹のタートル間に線が引かれます。NonSynchro 命令を実行すれば、シンクロ状態を抜けます。初期状態はシンクロ状態ではありません。例えば次のように使います。
<![CDATA[
CS PU FD 100 PD UP 90 ST2 UP2 90
SYNCHRO
REPEAT 36 [FD 10 RT 10 FD2 10 RT2 10]
NONSYNCHRO
]]>
で円柱を描きます。
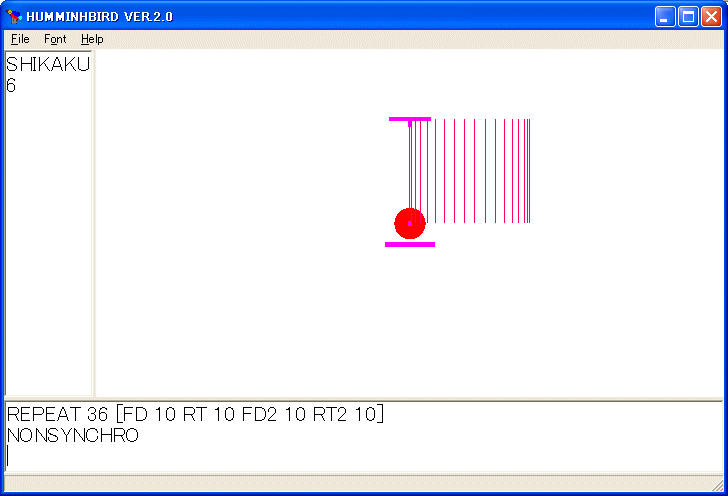
円柱に見えませんね。カメラを移動してみましょう。
<![CDATA[
FOR :I=0 TO 360 [LOOKAT 500*COS :I 500*SIN :I 500 0 0 0 0 1 0]
]]>
面白いでしょう。絵ではお見せできませんから、是非実行してみて下さい。
ヘリコプターが重心にいるとき、ヘリコプターが外接円の半径が :R の正 :N 角形を描くプログラムは
<![CDATA[
TO POLY :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH2 PU2 FD2 :R RT2 90 + 180 / :N PD2
REPEAT :N [FD2 :S RT2 360 / :N]
PU2 POP2 PD2
END
]]>
で与えられるので、高さ :H 、外接円の半径 :R の正 :N 角錐を描くプログラムは
<![CDATA[
TO PYRAMID :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH2 PU2 FD2 :R RT2 90 + 180 / :N PD2
REPEAT :N [FD2 :S RT2 360 / :N]
PUSH PU UP 90 FD :H PD
SYNCHRO
REPEAT :N [FD2 :S RT2 360 / :N]
NONSYNCHRO
PU2 POP2 PD2 PU POP PD
END
]]>
で与えられます。
<![CDATA[
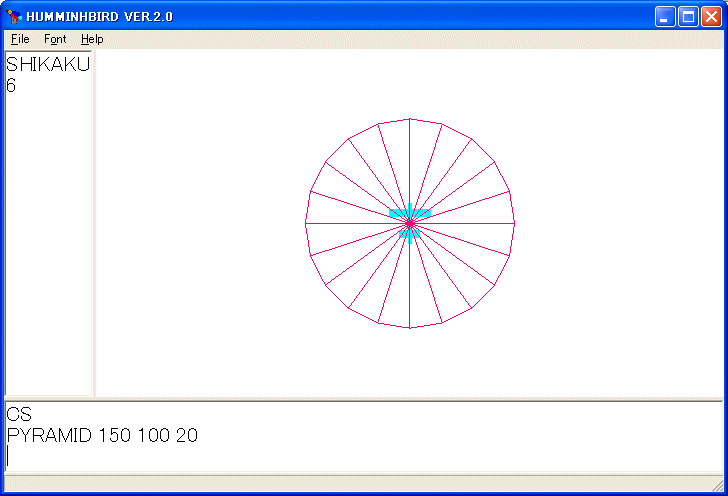
PYRAMID 150 100 20
]]>
を実行しました。マウスで回転すると
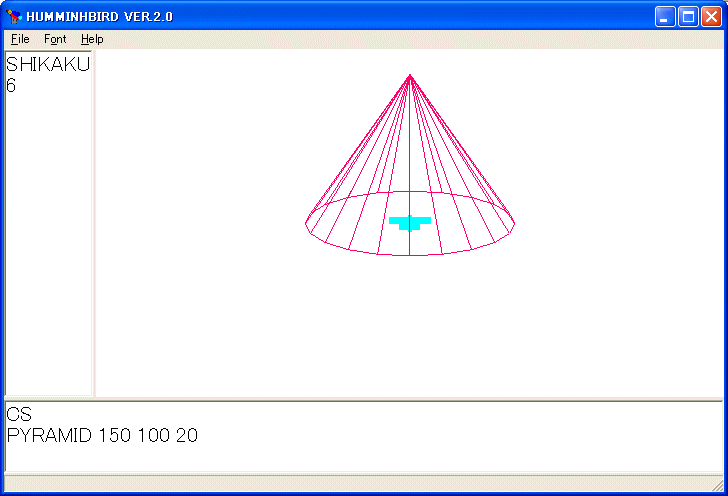
確かに正 20 角錐です。
<![CDATA[
PUSH PU UP 90 FD :H PD
SYNCHRO
REPEAT :N [FD2 :S RT2 360 / :N]
NONSYNCHRO
]]>
の部分で、飛行機を重心上 :H の所に移動させ、SYNCHRO と NONSYNCHRO で囲んでヘリコプターに正 :N 角形を描かせることにより、正 :N 角錐の稜線を描いています。SYNCHRO が実行されるとヘリコプターが移動したとき、飛行機とヘリコプターのペンが下りていれば、飛行機とヘリコプターの間に線が引かれます。飛行機が移動しても何も起こりません。この状態を抜けるのに NONSYNCHRO 命令を使います。上のプログラムを更に次のように修正します。
<![CDATA[
TO PYRAMID2 :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH2 PU2 FD2 :R RT2 90 + 180 / :N PD2
POLYMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONPOLYMODE
PUSH PU UP 90 FD :H PD
SYNCHRO SURFMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONSYNCHRO NONSURFMODE
PU2 POP2 PD2 PU POP PD
END
]]>
<![CDATA[
SETCOLOR 0 0 1
PYRAMID2 150 100 40
]]>
を実行し、マウスで回転すると次の図を描きます。
<![CDATA[
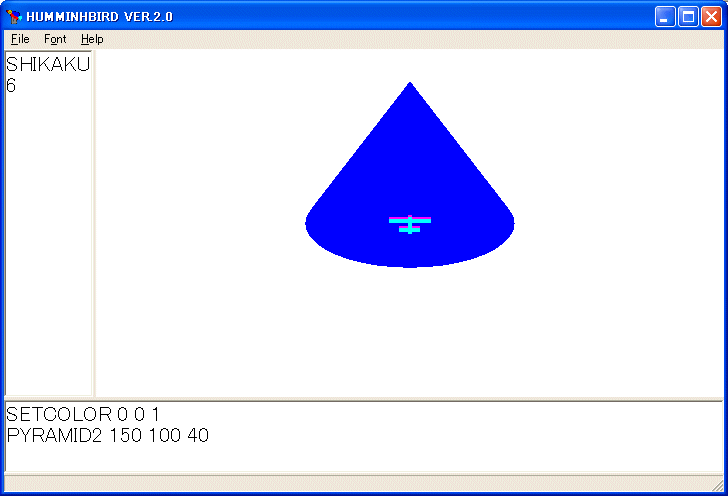
POLYMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONPOLYMODE
]]>
の部分で底面を描いています。POLYMODE と NONPOLYMODE で囲んで凸多角形を描くとその面が現在の色で塗りつぶされます。
<![CDATA[
SYNCHRO SURFMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONSYNCHRO NONSURFMODE
]]>
の部分で側面を描いています。SYNCHRO SURFMODE を実行すると、飛行機とヘリコプターのペンが下りていれば、飛行機またはヘリコプターが移動したとき、移動したタートルの元の位置と移動先と他のタートルの位置を結んでできる三角形を現在の色で塗りつぶします。 NONSYNCHRO NONSURFMODE を実行するとこの状態を抜けます。
単調な図形で何を描いているかはっきりしません。光を当てるには
<![CDATA[
ENABLELIGHTING
]]>
を実行します。次のように立体的な円錐に見えるようになりました。
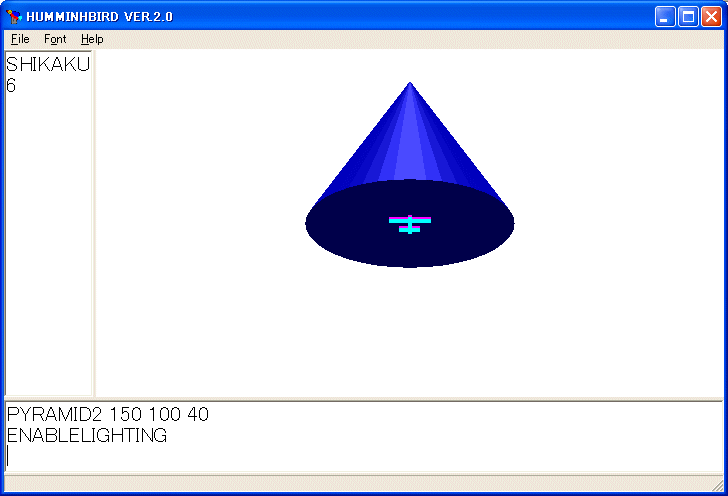
元に戻すには
<![CDATA[
DISABLELIGHTING
]]>
を実行します。
HUMMINGBIRD は OpenGL を使って作っていて、OpenGL の持っている機能の一部が使えます。
材質の設定と光源の設定ができます。
<![CDATA[
光源特性
AMBIENT 環境光成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
デフォルト： 0.1, 0.1, 0.1, 1.0
DIFFUSE 拡散成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
デフォルト： 0.8, 0.8, 0.8, 1.0
SPECULAR 鏡面成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
デフォルト： 0.3, 0.3, 0.3, 0.3
POSITION 平行光源の場合
光源の方向ベクトル＋ 0.0
デフォルト： 0.0 , 0.0, 1.0, 0.0
点光源の場合
点光源の位置＋ 1.0
デフォルト：平行光源の場合
]]>
<![CDATA[
材質の設定
AMBIENT 環境光反射成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
DIFFUSE 拡散反射成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
SPECULAR 鏡面反射成分の設定
設定値は R, G, B, A 強度を 0.0 から 1.0 までの数値で指定
デフォルト： 1.0, 1.0, 1.0, 1.0
SHININESS 鏡面反射光の鋭さを 0.0 から 128.0 までの数値で設定
デフォルト： 20.0
]]>
が設定できます。光源は 0 から 7 までの 8 個が使えます。デフォルト（初期設定）では 0 番目の光源だけが実行可能になっています。
光源は
<![CDATA[
ENABLELIGHT 式
]]>
で式の値の番号の光源が点きます。
<![CDATA[
DISABLELIGHT 式
]]>
で式の値の番号の光源が消えます。
<![CDATA[
SETLIGHTAMBIENT 式1 式2 式3 式4 式5
]]>
で式1 の値の番号の光源の AMBIENT の R 、G、 B、 A 値を式2 の値、式3 の値、式4 の値、式5 の値で設定します。
<![CDATA[
SETLIGHTDIFFUSE 式1 式2 式3 式4 式5
]]>
で式1 の値の番号の光源の DIFUUSE の R 、G、 B、 A 値を式2 の値、式3 の値、式4 の値、式5 の値で設定します。
<![CDATA[
SETLIGHTSPECULATR 式1 式2 式3 式4 式5
]]>
で式1 の値の番号の光源の SPECULAR の R 、G、 B、 A 値を式2 の値、式3 の値、式4 の値、式5 の値で設定します。
<![CDATA[
SETLIGHTPOSITION 式1 式2 式3 式4 式5
]]>
で式1 の値の番号の光源の POSITION の X 、 Y、 Z、 W 値を式2 の値、式3 の値、式4 の値、式5 の値で設定します。W は 0.0 か 1.0 で、W が 0.0 のときは X 、Y、 Z値は平行光源のある方向を示すベクトルを指定し、W が 1.0 のときは X 、Y、 Z値は点光源のある位置の座標を指定します。
<![CDATA[
SETLIGHT 式1 式2 式3 式4 式5 式6 式7 式8 式9 式10 式11 式12
式13 式14 式15 式16 式17
]]>
で式1 の値の番号の光源の AMBIENT 、DIFFUSE 、SPECULAR 、POSITION の値を一括して設定します。
材質の特性のうち AMBIENT と DIFFUSE はデフォルト（NONSHADINGMODE 実行時）では現在の色を使い、SPECULAR と SHININESS はデフォルトの値を使います。
<![CDATA[
SETDEFAULTSPECULATR 式1 式2 式3 式4
]]>
ですべての図形に共通するデフォルトの SPECULAR の R 、G、 B、 A 値を式1 の値、式1 の値、式3 の値、式4 の値で設定します。式4 の値は設定するだけで使いません。
<![CDATA[
SETDEFAULTSHININESS 式1
]]>
ですべての図形に共通するデフォルトの SHININESS の値を式1 の値で設定します。
<![CDATA[
SHADINGMODE
]]>
を実行すると各面の材質の特性値：AMBIENT 、DIFFUSE 、SPECULAR 、SHININESS を設定できます。デフォルトに戻すには
<![CDATA[
NONSHADINGMODE
]]>
を実行します。
<![CDATA[
SETAMBIENT 式1 式2 式3 式4
]]>
で面の材質の AMBIENT の R 、G、 B、 A 値を式1 の値、式2 の値、式3 の値、式4 の値で設定します。式4 の値は混色モードのとき、半透明な状態を表現するのに使います。
<![CDATA[
SETDIFFUSE 式1 式2 式3 式4
]]>
で面の材質の DIFFUSE の R 、G、 B、 A 値を式1 の値、式2 の値、式3 の値、式4 の値で設定します。式4 の値は混色モードのとき、半透明な状態を表現するのに使います。
<![CDATA[
SETSPECULATR 式1 式2 式3 式4
]]>
で面の材質の SPECULAR の R 、G、 B、 A 値を式1 の値、式2 の値、式3 の値、式4 の値で設定します。式4 の値は混色モードのとき、半透明な状態を表現するのに使います。
<![CDATA[
SETSHININESS 式
]]>
で面の材質の SHININESS の値を式の値で設定します。
<![CDATA[
NONSHADINGMODE
]]>
でデフォルトの状態に戻ります。
<![CDATA[
ENABLELIGHTING
SHADINGMODE
SETAMBIENT 0.19225 0.19225 0.19225 1.0
SETDIFFUSE 0.50754 0.50754 0.50754 1.0
SETSPECULAR 0.508273 0.508273 0.508273 1.0
SETSHININESS 51.2
SETLIGHTAMBIENT 0 0 0 0 1
SETLIGHTDIFFUSE 0 1 1 1 1
SETLIGHTSPECULAR 0 1 1 1 1
SETLIGHTPOSITION 0 1 1 1 0
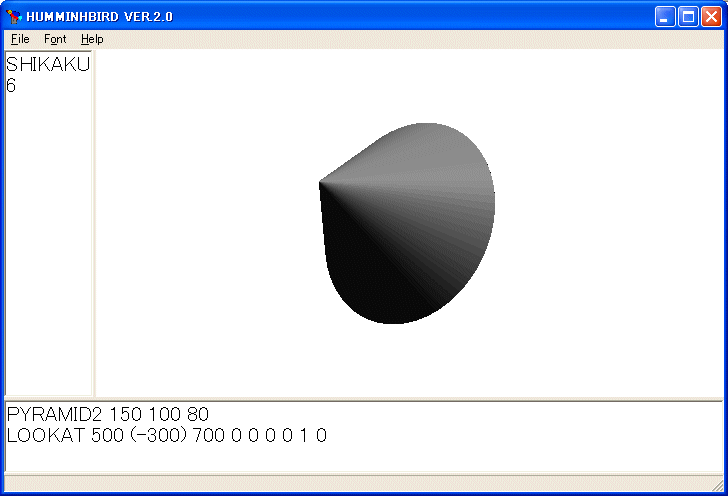
PYRAMID2 150 100 80
LOOKAT 500 (-300) 700 0 0 0 0 1 0
]]>
を実行すると次のようになります。
高さ :H 、外接円の半径 :R の正 :N 角柱を描くプログラムは
<![CDATA[
TO PRISM :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH PU UP 90 FD :H DOWN 90 FD :R RT 90 + 180 / :N PD
REPEAT :N [FD :S RT 360 / :N]
PUSH2 PU2 FD2 :R RT2 90 + 180 / :N PD2
REPEAT :N [FD2 :S RT2 360 / :N]
SYNCHRO
REPEAT :N [FD :S FD2 :S RT 360 / :N RT2 360 / :N]
NONSYNCHRO
PU2 POP2 PD2 PU POP PD
END
]]>
で与えられます。
<![CDATA[
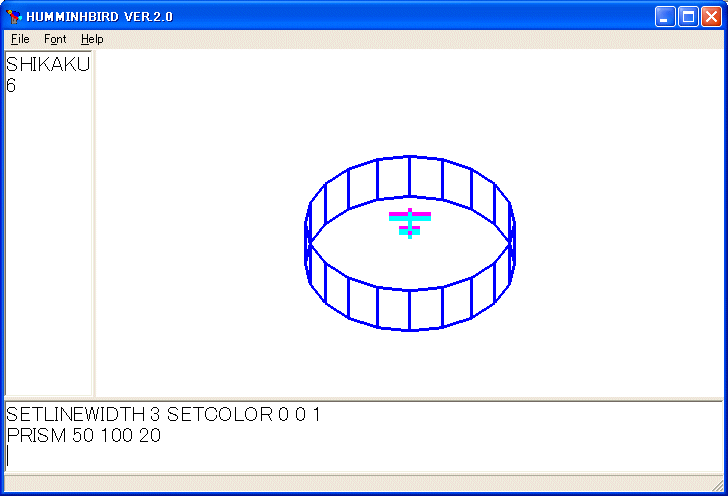
SETLINEWIDTH 3 SETCOLOR 0 0 1
PRISM 50 100 20
]]>
を実行し、マウスで回転しました。この図が簡単に描けるように、
<![CDATA[
SYNCHRO
REPEAT :N [FD :S FD2 :S RT 360 / :N RT2 360 / :N]
NONSYNCHRO
]]>
で、ヘリコプターが移動したときだけ、線を描くようにしています。
高さ :H 、外接円の半径 :R の正 :N 角反柱を描くプログラムは
次のように修正します。
<![CDATA[
TO PRISM2 :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH PU UP 90 FD :H DOWN 90 FD :R RT 90 + 180 / :N PD
REPEAT :N [FD :S RT 360 / :N]
PUSH2 PU2 RT2 180 / :N FD2 :R RT2 90 + 180 / :N PD2
REPEAT :N [FD2 :S RT2 360 / :N]
SYNCHRO
REPEAT :N [FD :S FD2 0 FD2 :S RT 360 / :N RT2 360 / :N]
NONSYNCHRO
PU2 POP2 PD2 PU POP PD
END
]]>
<![CDATA[
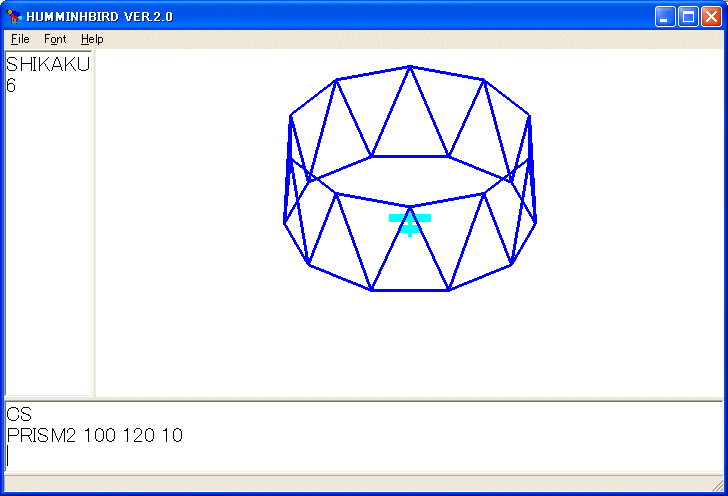
PRISM2 100 120 10
]]>
を実行し、マウスで回転しました。上のプログラムでは一見無駄に見える FD2 0 が必要です。面を塗りつぶすときは FD2 0 は必要ありません。
<![CDATA[
TO PRISM3 :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH PU UP 90 FD :H DOWN 90 FD :R LT 90 + 180 / :N PD
POLYMODE
REPEAT :N [FD :S LT 360 / :N]
NONPOLYMODE
RT 180 + 360 / :N
PUSH2 PU2 RT2 180 / :N FD2 :R RT2 90 + 180 / :N PD2
POLYMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONPOLYMODE
SYNCHRO SURFMODE
REPEAT :N [FD :S FD2 :S RT 360 / :N RT2 360 / :N]
NONSYNCHRO NONSURFMODE
PU2 POP2 PD2 PU POP PD
END
]]>
HUMMINGBIRD を新たに立ち上げ、
<![CDATA[
SETCOLOR 1 1 0
ENABLELIGHTING
PRISM3 100 120 10
LOOKAT 100 (-100) 200 0 0 0 0 1 0
]]>
を実行すると次の図を描きます。
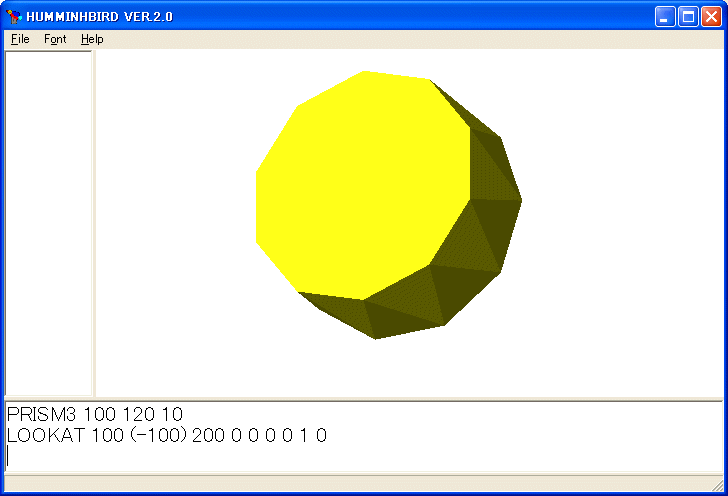
光源が点灯しているとき、POLYMODE と NONPOLYMODE で囲まれた凸多角形は裏と表があり、時計回りに回っている面が裏で、反時計回りに回っている面が表です。
SYNCHRO SURFMODE と NONSYNCHRO NONSURFMODE で囲まれているときは、飛行機が移動してできる三角形は飛行機の進んだ向きに回転下向きが反時計回りであれば表で、時計回りであれば裏ですが、ヘリコプターが移動してできる三角形はヘリコプターの進んだ向きに回転下向きが反時計回りであれば裏で、時計回りであれば表と逆になります。
光を消し、各面に異なる色を塗るなら、面の裏表を考慮する必要はありません。
単に次のプログラムで大丈夫です。
<![CDATA[
TO PRISM4 :H :R :N
LOCAL :S
:S = 2 * :R * COS 90 - 180 / :N
PUSH PU UP 90 FD :H DOWN 90 FD :R RT 90 + 180 / :N PD
SETCOLOR RAND RAND RAND
POLYMODE
REPEAT :N [FD :S RT 360 / :N]
NONPOLYMODE
PUSH2 PU2 RT2 180 / :N FD2 :R RT2 90 + 180 / :N PD2
SETCOLOR RAND RAND RAND
POLYMODE
REPEAT :N [FD2 :S RT2 360 / :N]
NONPOLYMODE
SYNCHRO SURFMODE
REPEAT :N [
SETCOLOR RAND RAND RAND FD :S
SETCOLOR RAND RAND RAND FD2 :S
RT 360 / :N RT2 360 / :N
]
NONSYNCHRO NONSURFMODE
PU2 POP2 PD2 PU POP PD
END
]]>
<![CDATA[
DISABLELIGHTING
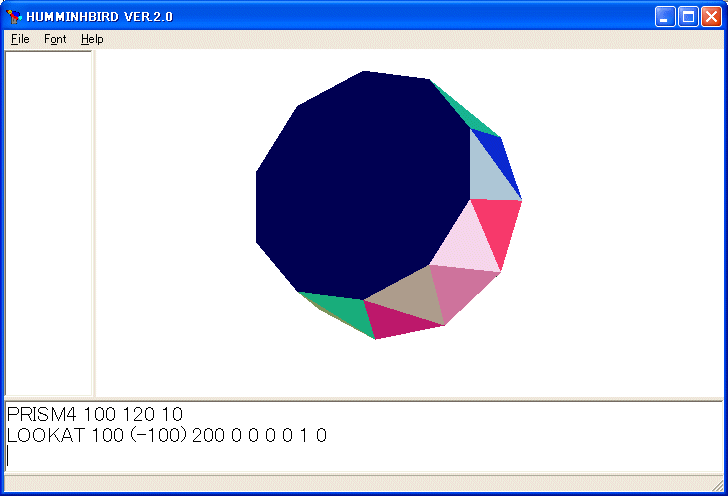
PRISM4 100 120 10
LOOKAT 100 (-100) 200 0 0 0 0 1 0
]]>
を実行すると次の図を描きます。
再帰呼び出しについて補足しておきます。
一辺 :SIZE で回転角 :ANGLE の（星形）正多角形を描くプログラムを再帰的に定義することができます。
<![CDATA[
TO POLY4 :SIZE :ANGLE :TOTAL
LOCAL :S
IF :TOTAL == 0 [
:S = 2 * :SIZE * COS (180 - :ANGLE)/2
PUSH PU FD :SIZE RT 90 + :ANGLE/2 PD
]
FD :SIZE RT :ANGLE
:TOTAL = :TOTAL + :ANGLE
IF :TOTAL % 360 == 0 [
PU POP PD STOP
]
POLY4 :SIZE :ANGLE :TOTAL
END
]]>
<![CDATA[
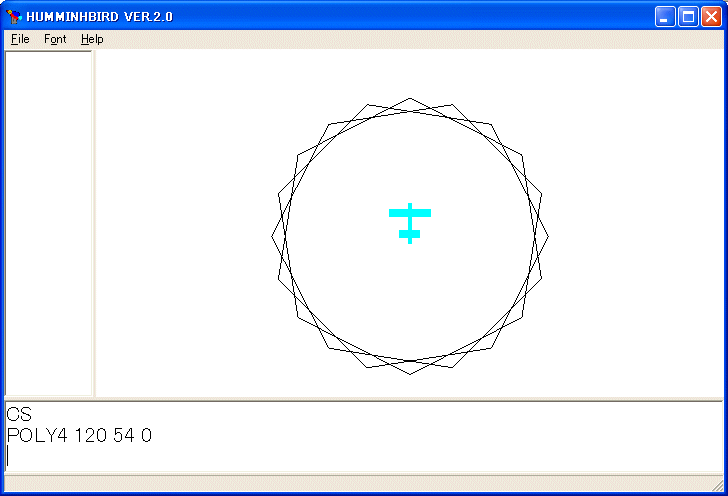
POLY4 120 54 0
]]>
を実行しました。POLY4 は引数に回転角の総量を表す :TOTAL を持っています。:TOTAL が 0 のとき
<![CDATA[
IF :TOTAL == 0 [
:S = 2 * :SIZE * COS (180 - :ANGLE)/2
PUSH PU FD :SIZE RT 90 + :ANGLE/2 PD
]
]]>
で初期設定をし、:TOTAL が 360 の倍数になったとき
<![CDATA[
IF :TOTAL % 360 == 0 [
PU POP PD STOP
]
]]>
で後始末します。STOP を実行すると手続きを終了します。:TOTAL が 360 の倍数でないときは
<![CDATA[
POLY4 :SIZE :ANGLE :TOTAL
]]>
で再帰呼び出しをしています。再帰呼び出しが END 行の一つ前だけに現れる場合を終端再帰（Tail recursion）といいます。HUMMINGBIRD は終端再帰の場合、再帰としての扱いでなく、繰り返しとして処理しています。上のプログラムを
<![CDATA[
TO POLY5 :SIZE :ANGLE :TOTAL
LOCAL :S
IF :TOTAL == 0 [
:S = 2 * :SIZE * COS (180 - :ANGLE)/2
PUSH PU FD :SIZE RT 90 + :ANGLE/2 PD
]
FD :SIZE RT :ANGLE
:TOTAL = :TOTAL + :ANGLE
IF :TOTAL % 360 == 0 [
PU POP PD
][
POLY5 :SIZE :ANGLE :TOTAL
]
END
]]>
と IF 文の第二の形式
<![CDATA[
IF 条件式 [命令の並び] [命令の並び]
]]>
を使っても定義できます。この IF 文は条件式が真のときは最初の命令の並びを実行し、偽のときは後ろの命令の並びを実行します。このように定義すると終端再帰にはなりません。再帰呼び出しの回数が少ないときは問題がありませんが、再帰呼び出しの回数が多くなると記憶領域を使い切って、HUMMINGBIRD が動かなくなります。
再帰呼び出しが END 行の一つ前だけに現れる場合に、再帰呼び出しの後ろに何か命令の並びがあっても HUMMINGBIRD は終端再帰（Tail recursion）と誤認し、再帰呼び出しの後ろの命令の並びは無視するので注意して下さい。
再帰呼び出しは慣れるまでは大変ですが、非常に強力なプログラミング技能です。再帰呼び出しなしには面白いプログラムは作れません。再帰呼び出しを使うと簡単なプログラムで複雑な図形が描けます。 タートル・グラフィックスではフラクタルな図形が簡単に描けます。まず木を描くプログラムです。
<![CDATA[
TO TREE :X :L
IF :L == 0 [STOP]
FD :X RT 30
TREE :X * 0.75 :L-1
LT 60
TREE :X * 0.75 :L-1
RT 30 BK :X
END
]]>
<![CDATA[
PU BK 120 PD TREE 70 8
]]>
を実行しました。TREE は仮引数を二つ持っていて、:L は木を何段階まで描くかのパラメータです。レベル :L が 0 なら何もしません。レベル :L が 0 でなければ :X だけ前進し右に 30 度回転し、大きさが 75 パーセントのレベル :L-1 の木を描き、左に 60 度回転し、大きさが 75 パーセントのレベル :L-1 の木を描き、右に 30 度回転し、 :X だけ後退し元の位置に戻ります。元の位置に戻ることがポイントです。
このような抽象的（間接的）な定義でコンピュータを動かせることを納得することが重要です。たくさん例を打ち込んで動かしていくうちに慣れて、当たり前のように思うようになります。
角度を変えたり、子供の木の大きさを変えたり、子供の木の個数を変えたりすることにより色々な木を描くことができます。例えば、次のように定義します。
<![CDATA[
TO TREE2 :X :L
IF :L == 0 [
LT 30 REPEAT 60[FD 0.3 RT 1] RT 120 REPEAT 60[FD 0.3 RT 1] RT 150
STOP
]
FD :X RT 45
TREE2 :X * 0.7 :L-1
LT 90
TREE2 :X * 0.7 :L-1
RT 45 BK :X
END
]]>
<![CDATA[
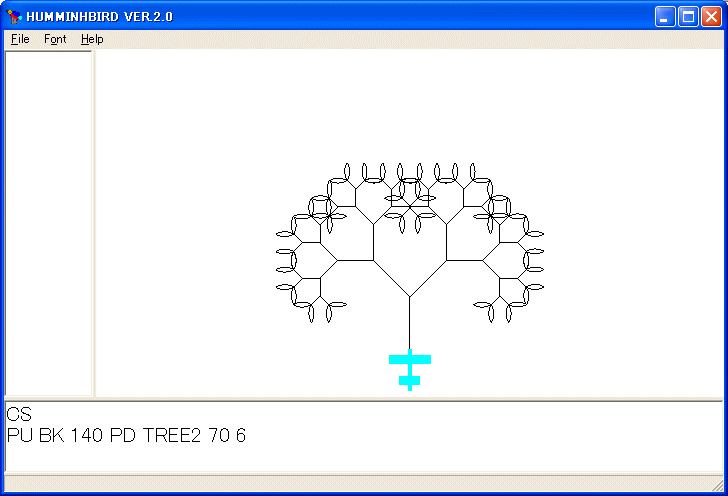
PU BK 140 PD TREE2 70 6
]]>
を実行しました。
次はコッホ曲線を描くプログラムです。
<![CDATA[
TO KOCH :SIZE :LEVEL
IF :LEVEL == 0 [FD :SIZE STOP]
KOCH :SIZE/3 :LEVEL-1
LT 60
KOCH :SIZE/3 :LEVEL-1
RT 120
KOCH :SIZE/3 :LEVEL-1
LT 60
KOCH :SIZE/3 :LEVEL-1
END
]]>
<![CDATA[
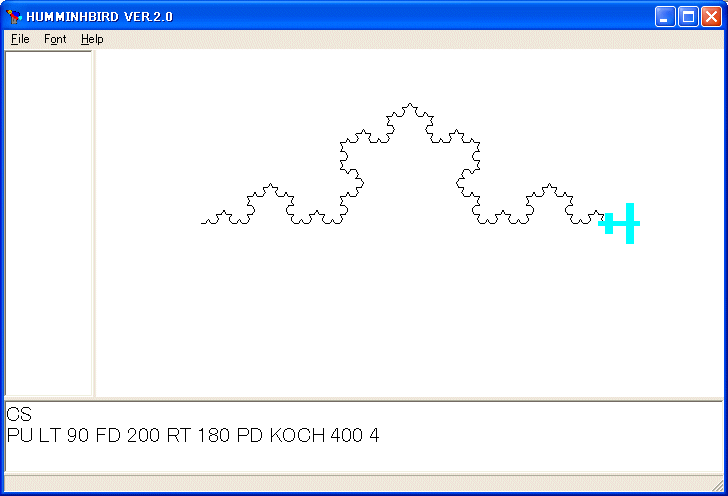
PU LT 90 FD 200 RT 180 PD KOCH 400 4
]]>
を実行しました。KOCH は二つの引数 :SIZE と :LEVEL を持っていて、 :SIZE でトータルの進む長さを、 :LEVEL で何段階まで描くかのレベルを指示します。:LEVEL が 0 ならば、 :SIZE だけ進んで止まります。:LEVEL が 0 でなければ、三分の一の長さでレベルが :LEVEL-1 のコッホ曲線四個を中央の二個を折り曲げて描きます。コッホ曲線は元には戻りません。
<![CDATA[
PU BK 120 PD REPEAT 3 [KOCH 240 3 RT 120]
]]>
を実行すると
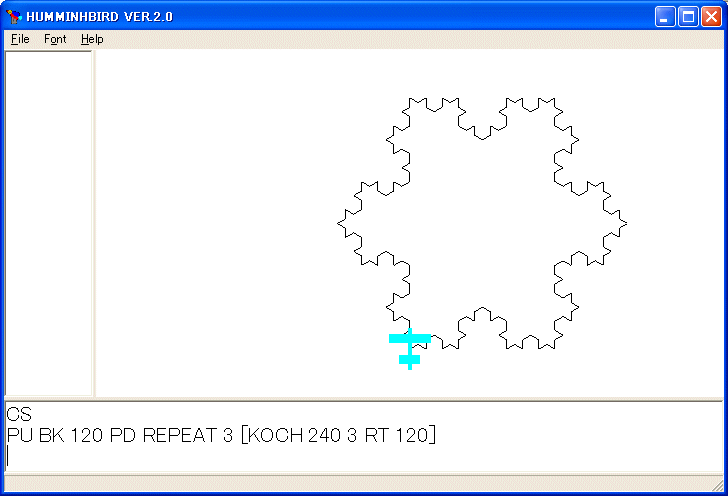
を描きます。さらに、
<![CDATA[
PU BK 120 PD REPEAT 3 [KOCH 240 3 LT 120]
]]>
を実行すると
を描きます。
次にＣ曲線を描くプログラムです。
<![CDATA[
TO C :SIZE :LEVEL
IF :LEVEL == 0 [FD :SIZE STOP]
C :SIZE :LEVEL-1
RT 90
C :SIZE :LEVEL-1
LT 90
END
]]>
<![CDATA[
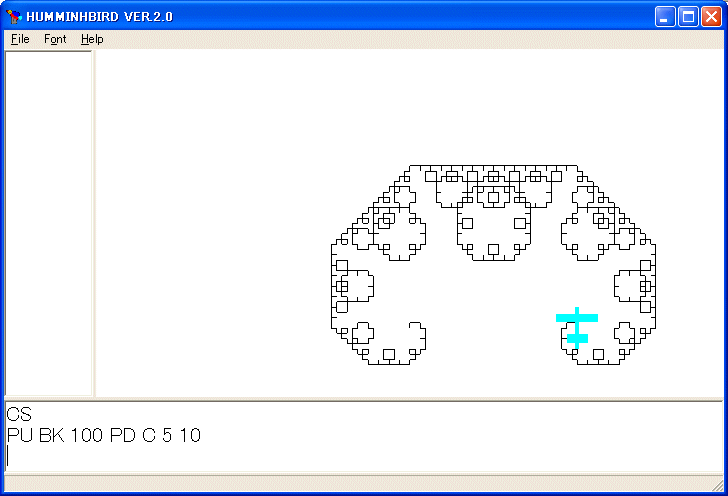
PU BK 100 PD C 5 10
]]>
を実行しました。この C 曲線はこのプログラムから描かれる図形をイメージするのが難しいです。線分からはじめて、中点をつかみ、直角になるまで引っ張る、つぎに出来た二つの線分に対して、中点をつかみ、直角になるまで引っ張る、という操作を繰り返してできる図形です。再帰呼び出しは繰り返しを表現する一つの技法です。
次にドラゴン曲線を描くプログラムです。
<![CDATA[
TO LDRAGON :SIZE :LEVEL
IF :LEVEL == 0 [FD :SIZE STOP]
LDRAGON :SIZE :LEVEL-1
RT 90
RDRAGON :SIZE :LEVEL-1
END
TO RDRAGON :SIZE :LEVEL
IF :LEVEL == 0 [FD :SIZE STOP]
LDRAGON :SIZE :LEVEL-1
LT 90
RDRAGON :SIZE :LEVEL-1
END
]]>
<![CDATA[
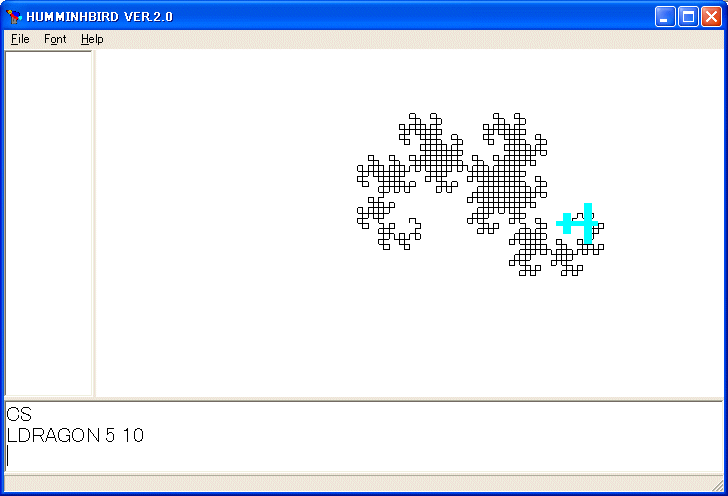
LDRAGON 5 10
]]>
を実行しました。ドラゴン曲線は描かれる図形が西洋の竜に似ていることから名付けられた曲線です。
次は有名なヒルベルト曲線です。
<![CDATA[
TO LHILBERT :SIZE :LEVEL
IF :LEVEL == 0 [STOP]
LT 90
RHILBERT :SIZE :LEVEL-1
FD :SIZE
RT 90
LHILBERT :SIZE :LEVEL-1
FD :SIZE
LHILBERT :SIZE :LEVEL-1
RT 90 FD :SIZE
RHILBERT :SIZE :LEVEL-1
LT 90
END
TO RHILBERT :SIZE :LEVEL
IF :LEVEL == 0 [STOP]
RT 90
LHILBERT :SIZE :LEVEL-1
FD :SIZE
LT 90
RHILBERT :SIZE :LEVEL-1
FD :SIZE
RHILBERT :SIZE :LEVEL-1
LT 90 FD :SIZE
LHILBERT :SIZE :LEVEL-1
RT 90
END
]]>
<![CDATA[
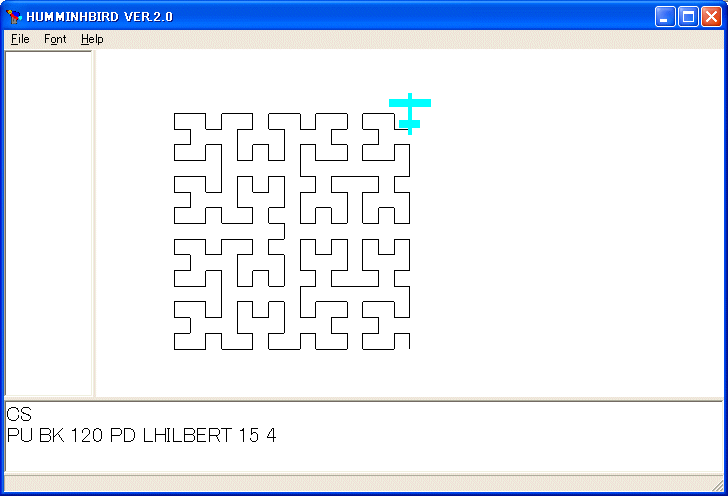
PU BK 120 PD LHILBERT 15 4
]]>
を実行しました。色々なレベルの図を HUMMINGBIRD に描かせてみて、プログラムと見比べてみながら、自分で描いてみるとプログラムの仕組みが理解できると思います。ドラゴン曲線と異なり､馴染みのある図形であることもありますが、プログラムの仕組みは理解しやすいです。
再帰を使ったフラクタルの例は昔沢山出版された LOGO の本に沢山載っていますし、PASCAL や C++ や Java の本にも結構載っています。LOGO の本格的な参考書は TURTLE GEOMETRY がお勧めです。それらのプログラムを HUMMINGBIRD のプログラムに変更するとき、LOGO のプログラムはだいたいそのまま、その他の言語のプログラムであれば、ずっと簡単な形に修正できると思います。
HUMMINGBIRD は以上のようなタートル・グラフィックスだけでなく、座標幾何学によるグラフィックスもサポートしています。
余弦関数 y=cos(x) のグラフは次のプログラムで描けます。
<![CDATA[
TO COS_GRAPH
LINE 0 200 0 0 (-200) 0
LINE -300 0 0 300 0 0
LOCAL :X :K1 :K2
:K1 = 300 / 4 / PI
:K2 = 100
RADIANMODE
PU SETPOS :K1 * (-4) * PI :K2 * COS -4 * PI 0 PD
FOR :X = -4 * PI TO 4 * PI STEP PI / 40 [
SETPOS :K1 * :X :K2 * COS :X 0
]
END
]]>
<![CDATA[
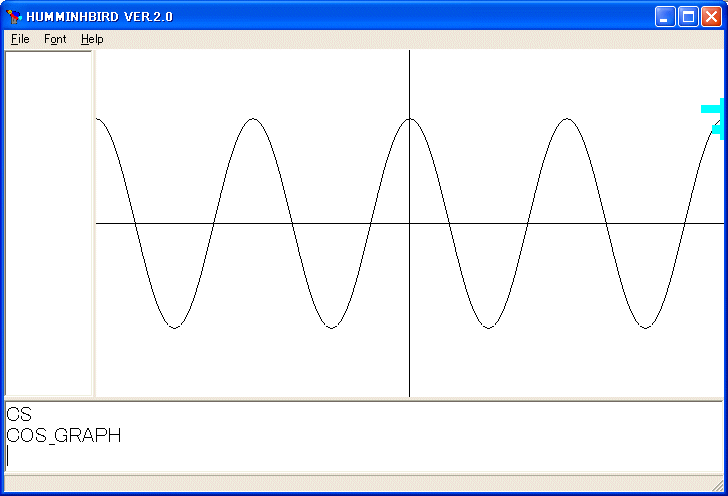
COS_GRAPH
]]>
を実行しました。
<![CDATA[
LINE 0 200 0 0 (-200) 0
LINE -300 0 0 300 0 0
]]>
で座標軸を描いています。LINE 命令は
<![CDATA[
LINE 式1 式2 式3 式4 式5 式6
]]>
の形式で使い、座標が（式1の値、 式2の値、 式3の値）の点と座標が（式4 の値、 式5 の値、 式3 の値）の点を結ぶ線分を描きます。座標が三次元になっているのは、HUMMINGBIRD はデフォルトで三次元ユークリッド空間のコンピュータ・グラフィックスを描くソフトだからです。-200 が括弧で囲われているのは、括弧がないと 0 - 200 が二つの実引数としてではなく、一つの実引数が式の形で与えられていると認識されるからです。
<![CDATA[
:K1 = 300 / 4 / PI
:K2 = 100
]]>
は x 軸と y 軸の拡大率です。
<![CDATA[
RADIANMODE
]]>
は三角関数や逆三角関数を度ではなく、ラジアンで考えるようにするための命令です。元に戻すには
<![CDATA[
DEGREEMODE
]]>
を実行します。
<![CDATA[
PU SETPOS :K1 * (-4) * PI :K2 * COS -4 * PI 0 PD
]]>
で飛行機を書き始めの位置にセットしています。SETPOS 命令は
<![CDATA[
SETPOS 式1 式2 式3
]]>
の形式で使い、座標が（式1の値、 式2の値、 式3の値）の点に飛行機を移動します。ペンが下りていれば線を描きます。
<![CDATA[
FOR :X = -4 * PI TO 4 * PI STEP PI / 40 [
SETPOS :K1 * :X :K2 * COS :X 0
]
]]>
で関数 y=\cos(x) のグラフを -4π <= x <= 4π の範囲で描きます。関数と範囲を入力すると何も考えなくてもきれいなグラフを描いてくれるソフトがたくさんフリーで出回っていますが、自分で少し苦労して描かせてみるのも、良い勉強になると思います。
余弦関数二つの和 y=cos(8x)+cos(9x) のグラフは次のプログラムで描けます。
<![CDATA[
TO COS_GRAPH2
LINE 0 200 0 0 (-200) 0
LINE -300 0 0 300 0 0
LOCAL :X :K1 :K2
:K1 = 300 / 4 / PI
:K2 = 70
RADIANMODE
PU SETPOS :K1 * (-4) * PI :K2 * COS -4 * PI 0 PD
FOR :X = -4 * PI TO 4 * PI STEP PI / 40 [
SETPOS :K1 * :X :K2 * ((COS 8 * :X) + COS 9 * :X) 0
]
END
]]>
<![CDATA[
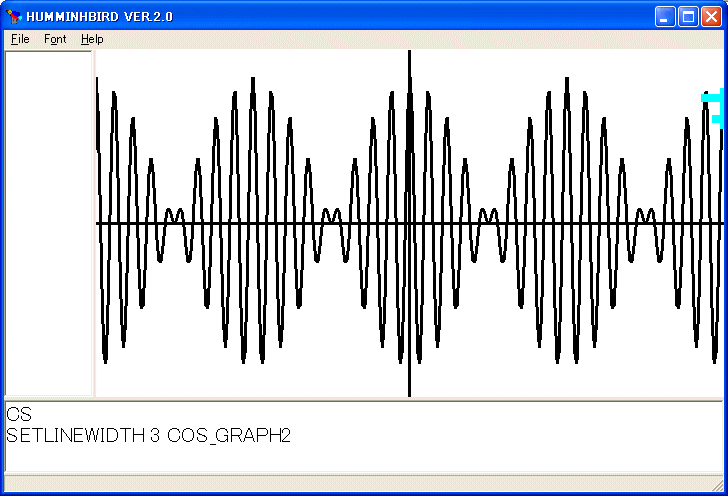
SETLINEWIDTH 3 COS_GRAPH2
]]>
を実行しました。ここで
<![CDATA[
SETPOS :K1 * :X :K2 * ((COS 8 * :X) + COS 9 * :X) 0
]]>
と COS 8 * :X が括弧で囲まれているのは COS の範囲を明示するためです。括弧がないと (COS ((8 * :X) + (COS (9 * :X))) と解釈されてしまいます。これは関数や手続きが引数を括弧で囲まなくて良いようにしたことの副作用です。通常のプログラミング言語と異なるところですから気を付けて下さい。
次にバラ曲線（正葉線）を描いてみます。媒介変数で与えられる曲線です。
<![CDATA[
TO ROSE :A
LOCAL :K :X :Y :T
:K=150 :T = 0
RADIANMODE
PU SETPOS :K 0 0 PD
DO [
:T = :T + PI/50
:X = :K*(COS :A*:T)*COS :T
:Y = :K*(COS :A*:T)*SIN :T
SETPOS :X :Y 0
] UNTIL ((ABS:X-:K)<0.01) && ((ABS :Y)<0.01)
DEGREEMODE
END
]]>
<![CDATA[
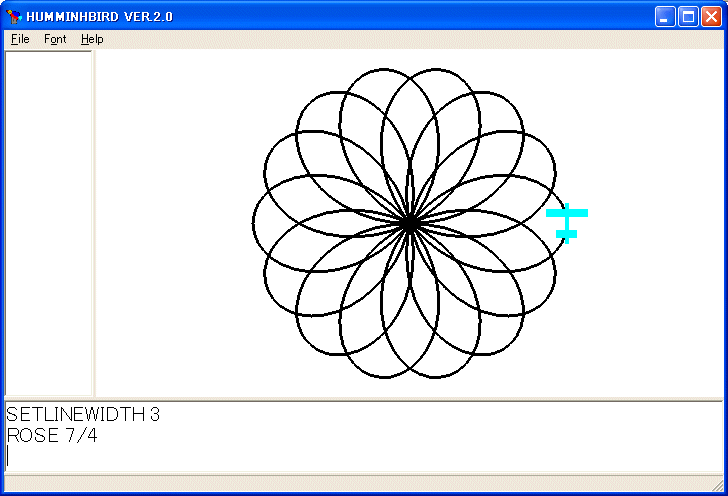
SETLINEWIDTH 3
ROSE 7/4
]]>
を実行しました。:A には正の有理数（整数か分数）を与えます。バラ曲線の全体が描かれたかどうかは、出発点に戻ったかどうかで判断し、コンピュータに調べさせています。:X = :K*(COS :A*:T)*COS :T と COS :A*:T が括弧で囲まれているのは COS の範囲を明示するためです。括弧がないと :X = :K*COS (:A*:T*COS :T) と解釈されてしまいます。
次にトロコイドを描いてみます。次の手続きは二つの引数を持っています。:A に正の有理数を与えたとき、:B の値に応じて、半径１の円の外側を半径 :A の円を転がしたとき、転がる円の内側（:B<1 のとき）か外側（:B>1 のとき）にある一点が描く軌跡である外トロコイドか、転がる円の円周上（:B==1 のとき）の一点が描く軌跡である外サイクロイドを描きます。:A に負の有理数を与えたとき、:B の値に応じて、半径１の円の外側を半径 -:A の円を転がしたとき、転がる円の内側（:B<1 のとき）か外側（:B>1 のとき）にある一点が描く軌跡である内トロコイドか、転がる円の円周上（:B==1 のとき）の一点が描く軌跡である内サイクロイドを描きます。
<![CDATA[
TO TROCHOID :A :B
LOCAL :X :Y :T :K :SX
:T = 0
RADIANMODE
IF :A > 0 [
:SX = ((1+:A)-:A*:B)
:K = 150 /(1+:A+:A*:B)
][
:SX = ((1+:A)+:A*:B)
IF -:A*(1+:B)-1 > 1 [
:K = 150 /(-:A*(1+:B)-1)
][
:K = 150
]
]
SETCOLOR 0 0 0
:SX = :K * :SX
PU SETPOS :SX 0 0 PD
DO [
:T = :T + PI/50
IF :A > 0 [
:X = :K*((1+:A)*(COS :T)-:A*:B*COS(1/:A+1)*:T)
:Y = :K*((1+:A)*(SIN :T)-:A*:B*SIN(1/:A+1)*:T)
SETPOS :X :Y 0
][
:X = :K*((1+:A)*(COS :T)+:A*:B*COS(-1/:A-1)*:T)
:Y = :K*((1+:A)*(SIN :T)-:A*:B*SIN(-1/:A-1)*:T)
SETPOS :X :Y 0
]
] UNTIL ((ABS:X-:SX)<0.01) && ((ABS :Y)<0.01)
SETCOLOR 1 0 0
PU SETPOS :K 0 0 PD
FOR :T = 0 TO 2*PI STEP PI/20 [
SETPOS :K*COS :T :K * SIN :T 0
]
SETCOLOR 0 0 0
DEGREEMODE
END
]]>
<![CDATA[
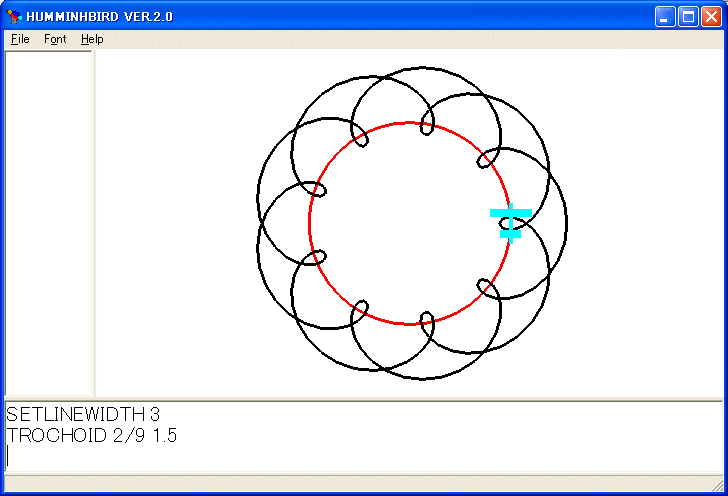
SETLINEWIDTH 3
TROCHOID 2/9 1.5
]]>
を実行しました。同じくトロコイドの全体が描かれたかどうかは、出発点に戻ったかどうかで判断し、コンピュータに調べさせています。
最後にリマソンを描いてみます。極座標で
<![CDATA[
r = a cos θ + b
]]>
で与えられる曲線です。a=b のときはカーディオイドといいます。
<![CDATA[
TO LIMACON :A :B
LOCAL :X :Y :T
RADIANMODE
PU SETPOS :A+:B 0 0 PD
FOR :T=0 TO 2*PI STEP PI/50 [
:X = (:A*(COS :T)+:B)*COS :T
:Y = (:A*(COS :T)+:B)*SIN :T
SETPOS :X :Y 0
]
DEGREEMODE
END
]]>
<![CDATA[
SETLINEWIDTH 3
LIMACON 140 70
]]>
を実行しました。
ユークリッド空間のプログラミングの最後に三次元のグラフを描いてみます。まず双曲放物面を描くプログラムです。
<![CDATA[
TO HYPERBOLIC_PARABOLOID
LOCAL :X :Y :DX :DY :K
:K = 50
:DX = 0.1 :DY = 0.1
SETCOLOR 1 0 0
FD 200 BK 400 FD 200 RT 90
FD 300 BK 600 FD 300 UP 90 FD 200 BK 400 FD 200
SETCOLOR 0 1 1
FOR :X=-2 TO 2 STEP :DX [
FOR :Y=-2 TO 2 STEP :DY [
PU SETPOS :K*:X :K*:Y :K*(-:X*:X+:Y*:Y) PD
POLYMODE
SETPOS :K*(:X+:DX) :K*:Y :K*(-(:X+:DX)*(:X+:DX)+:Y*:Y)
SETPOS :K*(:X+:DX) :K*(:Y+:DY)
:K*(-(:X+:DX)*(:X+:DX)+(:Y+:DY)*(:Y+:DY))
SETPOS :K*:X :K*:Y :K*(-:X*:X+:Y*:Y)
NONPOLYMODE
POLYMODE
SETPOS :K*(:X+:DX) :K*(:Y+:DY)
:K*(-(:X+:DX)*(:X+:DX)+(:Y+:DY)*(:Y+:DY))
SETPOS :K*:X :K*(:Y+:DY) :K*(-:X*:X+(:Y+:DY)*(:Y+:DY))
SETPOS :K*:X :K*:Y :K*(-:X*:X+:Y*:Y)
NONPOLYMODE
]
]
END
]]>
<![CDATA[
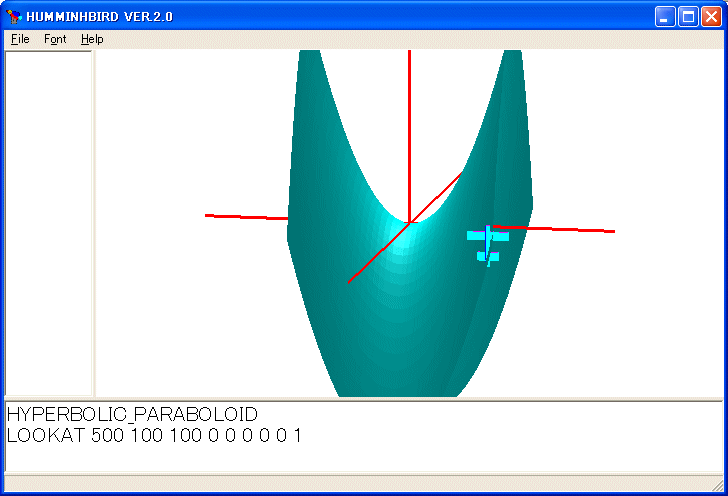
ENABLELIGHTING
HYPERBOLIC_PARABOLOID
LOOKAT 500 100 100 0 0 0 0 0 1
]]>
を実行すると次の図を描きます。
最後にトーラス（輪環面）を描くプログラムを与えます。
<![CDATA[
TO TORUS :R :T
LOCAL :U :V :DU :DV :K :X :Y :Z
:K = 50
:DU = PI/20 :DV = PI/20
RADIANMODE
FOR :V=0 TO 2*PI STEP :DV [
FOR :U=0 TO 2*PI STEP :DU [
:X = :K*(:R+:T*COS :U)*COS :V
:Y = :K*(:R+:T*COS :U)*SIN :V
:Z = :K*:T*SIN :U
PU SETPOS :X :Y :Z PD
POLYMODE
:X = :K*(:R+:T*COS :U)*COS :V+:DV
:Y = :K*(:R+:T*COS :U)*SIN :V+:DV
:Z = :K*:T*SIN :U
SETPOS :X :Y :Z
:X = :K*(:R+:T*COS :U+:DU)*COS :V+:DV
:Y = :K*(:R+:T*COS :U+:DU)*SIN :V+:DV
:Z = :K*:T*SIN :U+:DU
SETPOS :X :Y :Z
:X = :K*(:R+:T*COS :U)*COS :V
:Y = :K*(:R+:T*COS :U)*SIN :V
:Z = :K*:T*SIN :U
SETPOS :X :Y :Z
NONPOLYMODE
POLYMODE
:X = :K*(:R+:T*COS :U+:DU)*COS :V+:DV
:Y = :K*(:R+:T*COS :U+:DU)*SIN :V+:DV
:Z = :K*:T*SIN :U+:DU
SETPOS :X :Y :Z
:X = :K*(:R+:T*COS :U+:DU)*COS :V
:Y = :K*(:R+:T*COS :U+:DU)*SIN :V
:Z = :K*:T*SIN :U+:DU
SETPOS :X :Y :Z
:X = :K*(:R+:T*COS :U)*COS :V
:Y = :K*(:R+:T*COS :U)*SIN :V
:Z = :K*:T*SIN :U
SETPOS :X :Y :Z
NONPOLYMODE
]
]
END
]]>
<![CDATA[
ENABLELIGHTING
SETCOLOR 0 0 1
TORUS 2 1
LOOKAT 500 100 400 0 0 0 0 0 1
]]>
を実行すると次の図を描きます。
媒介変数の式で表される色々の三次元の図形を描下さい。どんな図形でも描けるようになっているはずです。
次に HUMMINGBIRD が活躍する三つの舞台を簡単に紹介します。いままで考察したのは二次元および三次元ユークリッド空間でした。ユークリッド空間は小学校以来のなじみのある空間です。
<![CDATA[
REPEAT 3 [FD 120 RT 120]
]]>
を実行すると一辺 120 の正三角形を描きます。
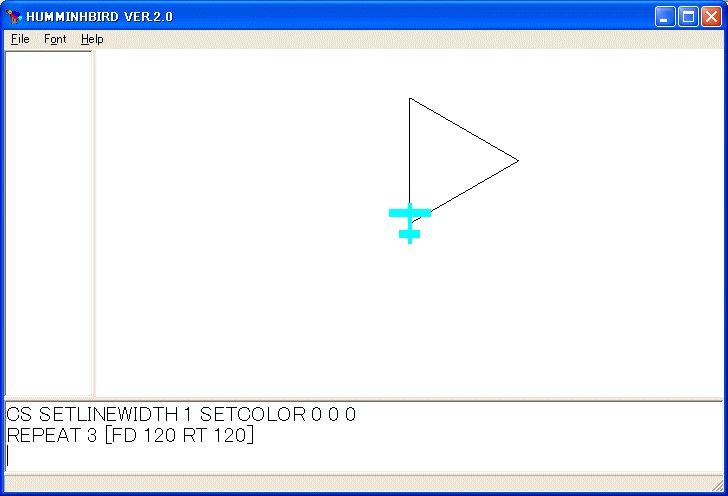
ユークリッド空間では一般に三角形（凸多角形でも同じことです）の外角の和は 360 度ですから正三角形を描くには 3 で割って 120 度づつ回転すれば良いです。
次に球面幾何学を考察します。
<![CDATA[
SETG_MODE 2
]]>
を実行します。
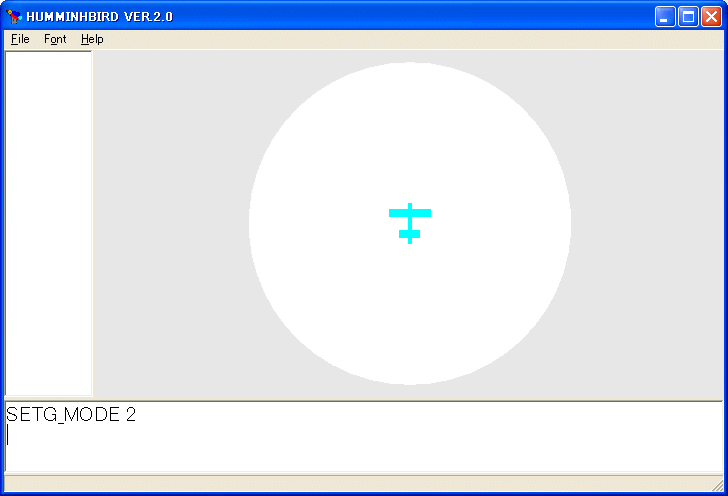
更に
<![CDATA[
ENABLELIGHTING
]]>
を実行します。
<![CDATA[
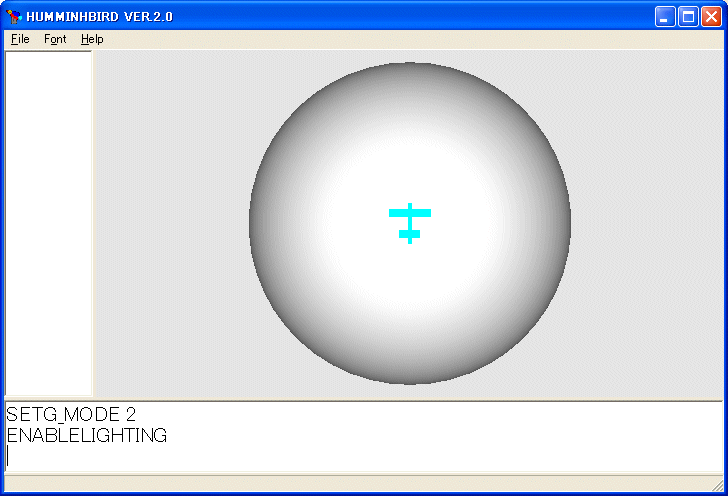
ENABLELIGHTING
]]>
を実行しないと球面が円板のように見えます。
今度はタートルは球面上（デフォルトでは単位球面：半径 1 の球面）を移動します。デフォルトではという意味は明示的に SETRADIUS 命令によって半径を変えなければと言う意味です。
<![CDATA[
SETRADIUS 式
]]>
の形式で球面の半径を式の値に変えることができます。
基本的な命令はユークリッド平面の時と同じです。ユークリッド空間に戻るには、
<![CDATA[
SETG_MODE 1
]]>
を実行します。単位球面上で正三角形を描くつもりで、
<![CDATA[
SETWIDTH 3
REPEAT 3 [FD 1 RT 120]
]]>
を実行すると次のようになります。
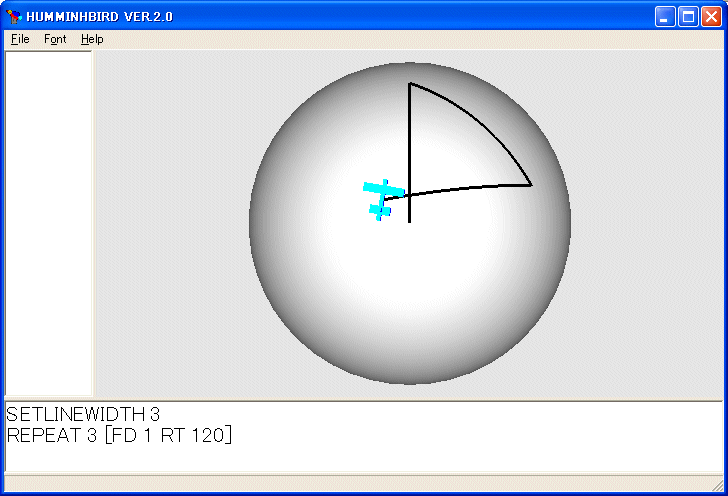
飛行機は元には戻りません。球面上の幾何学（球面幾何学）では、大円（球面の中心を通る平面と球面の交線）を直線と考え、大円の一部を線分と考えます。
△ABC は球面三角形とする時、∠A + ∠B + ∠C は 180 度ではありません。正確には、単位球面で考えた時、角度をラジアン（180 度 $= π ラジアン）ではかった時、∠A + ∠B + ∠C = π + △ABC となります。ここで π は円周率（3.141592653589793238462643383279・・・）で、
△ABC は球面三角形の面積です。したがって、∠A + ∠B + ∠C は
180 度より大きくなります。正確な正三角形を描く方法は後で考えます。
<![CDATA[
SETG_MODE 3
]]>
を実行します。画面が次のようになります。
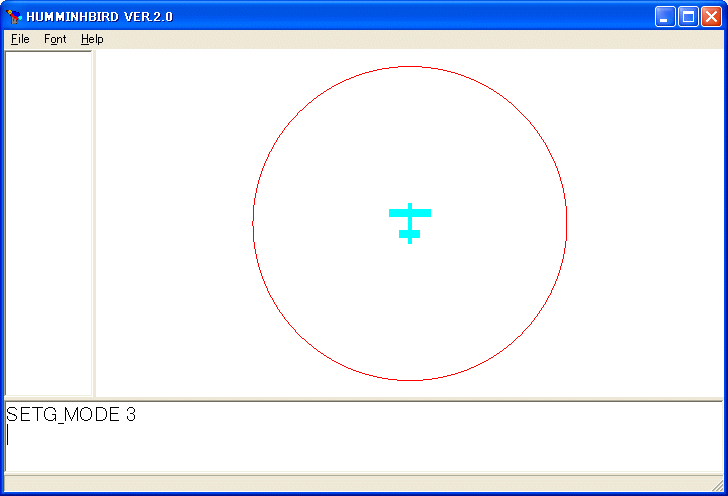
今度はタートルはポアンカレの円板モデル（正確には、三次元空間で、ポアンカレの球体モデルです）を移動します。基本的な命令はユークリッド空間の時と同じです。
今度も正三角形を描くつもりで、
<![CDATA[
REPEAT 3 [FD 2 RT 120]
]]>
を実行すると次のようになります。
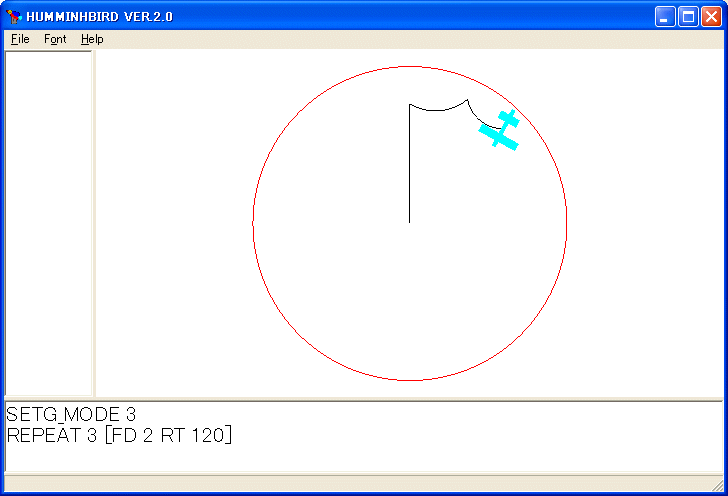
今度も飛行機は元には戻りません。ポアンカレの円板モデル（双曲幾何学）は、双曲平面を単位円板の中に押し込んだものです。双曲平面の一つの地図です。世界地図は色々ありますがどの地図も歪んでいて、距離と角の正確なものは無いように、双曲平面のこの地図も長さが歪んでいます。中心から外れるほど見た目の距離は小さくなります。
球面の中心からの双曲距離を x とし、見た目の距離（ユークリッド空間内の単位球面としての距離）を y とすると
<![CDATA[
y = (exp(x)-1)/(exp(x)+1)
x = log (1+y)/(1-y)
]]>
の関係があります。実はこのような関係式が成り立つ（y が 1 に非常に近い場合が多く大きな誤差が出る）ためにコンピュータでは誤差がすぐ累積して正確な図を描くのに苦労します。
角は見た目の通りです。ポアンカレの円板モデルでは
「円板の中心を通る直線」と「円板と両端で直交する円孤」を直線と考えます。ポアンカレの球体モデルでもその類比を直線と考えます。
△ABC は双曲三角形とする時、∠A + ∠B + ∠C は
180 度ではありません。正確には、角度をラジアン（180 度 = π ラジアン）で測った時、∠A + ∠B + ∠C = π - △ABC となります。ここで π は円周率で、
△ABC は双曲三角形の面積です。したがって、∠A + ∠B + ∠C は
180 度より小さくなります。
ユークリッド幾何学、球面幾何学および双曲幾何学における三角形について調べます。
ユークリッド幾何学の三角形の辺と角度の関係は
高等学校で習います。
△ABC は三角形で、辺 a は頂点 A に、辺 b は頂点 B に、
辺 c は頂点 C に対応するとする時、
正弦法則は
<![CDATA[
sin A/a = sin B/b = sin C/c
]]>
で、
余弦法則は
<![CDATA[
a^2 = b^2 + c^2 - 2bc cos A
b^2 = c^2 + a^2 - 2ca cos B
c^2 = a^2 + b^2 - 2ab cos C
]]>
となります。
高知大学教育学部にくる学生さん達は「数学とは公式を覚え、それを使って計算をするものだった」と口々に言いますが、公式を覚えるのでなく、それぞれの公式の導き方を覚えるようにすれば、自ずから数学において何が基礎・基本か自然と分かり、数学を楽しく学べるのではないかと思います。
これを使うと三辺 a,b,c が与えられた時、対応する角を余弦法則で
計算することが出来るので、この三角形を描く
プログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI :A :B :C
LOCAL :ALPHA :BETA :GAMMA
:ALPHA = ACOS (:B*:B+:C*:C-:A*:A)/(2*:B*:C)
:BETA = ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
:GAMMA = ACOS (:A*:A+:B*:B-:C*:C)/(2*:A*:B)
FD :A RT 180-:GAMMA FD :B RT 180-:ALPHA FD :C RT 180-:BETA
END
]]>
<![CDATA[
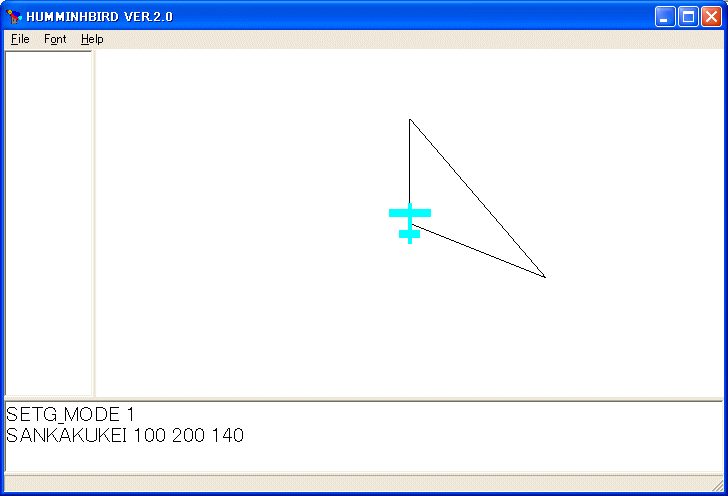
SANKAKUKEI 100 200 140
]]>
を実行すると次のような三角形を描きます。任意の二辺の和は他の辺より大きくなければなりません。
このプログラムを次のように修正します。
<![CDATA[
TO SANKAKUKEI2 :A :B :C :N
LOCAL :ALPHA :BETA :GAMMA :INDEX :K
:ALPHA = ACOS (:B*:B+:C*:C-:A*:A)/(2*:B*:C)
:BETA = ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
:GAMMA = ACOS (:A*:A+:B*:B-:C*:C)/(2*:A*:B)
FD :A/:N PUT 1 0 FD (:N-1)*:A/:N
RT 180-:GAMMA
FD :B/:N PUT 1 1 FD (:N-1)*:B/:N
RT 180-:ALPHA
FD :C/:N PUT 1 2 FD (:N-1)*:C/:N
RT 180-:BETA
:INDEX = 0
WHILE :INDEX <= 9 [
PU2 GET2 1 :INDEX PD2
FOR :K=1 TO 3 [
PU GET 1 :INDEX+:K%3 PD
TOWARD2
FD2 DISTANCE2/:N PUT2 1 :INDEX+:K+2 FD2 DISTANCE2
]
:INDEX = :INDEX+3
]
END
]]>
<![CDATA[
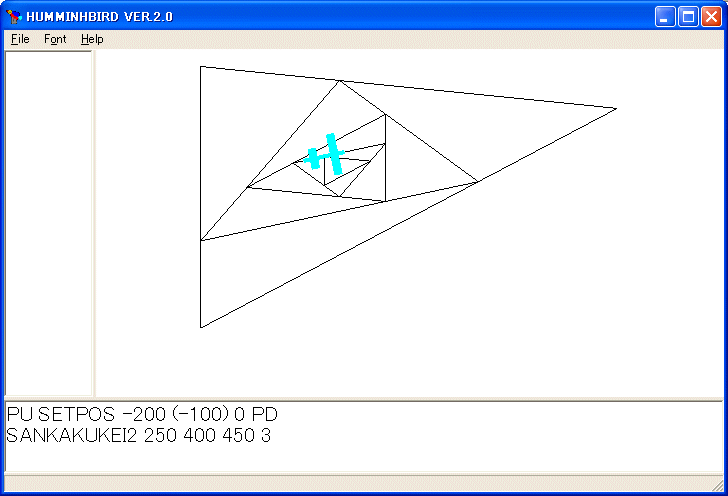
PU SETPOS -200 (-100) 0 PD
SANKAKUKEI2 250 400 450 3
]]>
を実行すると次のようなネストした三角形を描きます。
TOWARD2 命令は
<![CDATA[
TOWARD2
]]>
の形式で使い、ヘリコプターを飛行機の方に向けます。
DISTANCE2 関数は
<![CDATA[
DISTANCE2
]]>
の形式で使い、ヘリコプターから飛行機までの距離を与えます。
TOWARD 命令は
<![CDATA[
TOWARD 式1 式2 式3
]]>
の形式で使い、飛行機を（式1、 式2、 式3）で表される点の方に向けます。
DISTANCE 関数は
<![CDATA[
DISTANCE 式1 式2 式3
]]>
の形式で使い、飛行機から（式1、 式2、 式3）で表される点までの距離を与えます。
ユークリッド空間では三角形の三つの角度が与えられただけでは三角形は一意に決まりません。それらの三角形は相似三角形と呼ばれます。
次に球面幾何学の三角形を考察します。
単位球面上で考えます。余弦法則は二つあり、辺の余弦法則と角の余弦法則です。
△ABC は球面三角形で、辺 a は頂点 A に、辺 b は頂点 B に、
辺 c は頂点 C に対応するとする時、辺の余弦法則は
<![CDATA[
cos ∠a = cos ∠b cos ∠c + sin ∠b sin ∠c cos ∠A
cos ∠b = cos ∠c cos ∠a + sin ∠c sin ∠a cos ∠B
cos ∠c = cos ∠a cos ∠b + sin ∠a sin ∠b cos ∠C
]]>
で与えられます。角の余弦法則は
<![CDATA[
cos ∠A = - cos ∠B cos ∠C + sin ∠B sin ∠C cos ∠a
cos ∠B = - cos ∠C cos ∠A + sin ∠C sin ∠A cos ∠b
cos ∠C = - cos ∠A cos ∠B + sin ∠A sin ∠B cos ∠c
]]>
です。さらに、球面三角形の正弦法則
<![CDATA[
sin ∠a / sin ∠A = sin ∠b / sin ∠B = sin ∠c / sin ∠C
]]>
が成り立ちます｡
球面幾何学の三角形は、三つの辺の長さで決定できます｡対応する角の大きさは
辺の余弦法則で与えられます。三辺 :SIZE1、 :SIZE2、 :SIZE3 が与えられた
球面三角形を描くプログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI3 :SIZE1 :SIZE2 :SIZE3
LOCAL :A :B :C :ANGLE1 :ANGLE2 :ANGLE3
:A = :SIZE1 / RADIUS * 180 / PI
:B = :SIZE2 / RADIUS * 180 / PI
:C = :SIZE3 / RADIUS * 180 / PI
:ANGLE1 = ACOS ((COS :A)-(COS :B)*(COS :C))/((SIN :B)*(SIN :C))
:ANGLE2 = ACOS ((COS :B)-(COS :C)*(COS :A))/((SIN :C)*(SIN :A))
:ANGLE3 = ACOS ((COS :C)-(COS :A)*(COS :B))/((SIN :A)*(SIN :B))
:ANGLE1 = 180 - :ANGLE1
:ANGLE2 = 180 - :ANGLE2
:ANGLE3 = 180 - :ANGLE3
FD :SIZE1 RT :ANGLE3 FD :SIZE2 RT :ANGLE1 FD :SIZE3 RT :ANGLE2
END
]]>
局所変数 :A、 :B、 :C、 :ANGLE1、 :ANGLE2、 :ANGLE3 を宣言します。
HUMMINGBIRD の球面の半径 RADIUS （デフォルトは RADIUS = 1）を変更した場合は、辺の余弦法則を使うために、上のように補正が必要です。
:A、 :B、 :C にそれぞれ :SIZE1、 :SIZE2、 :SIZE3 に対応する中心角を
セットします。辺の余弦法則を使って、対応する内角 :ANGLE1、 :ANGLE2、 :ANGLE3 を
計算します｡ 三つの辺の長さ :SIZE1、 :SIZE2、 :SIZE3 と対応する内角
:ANGLE1、 :ANGLE2、 :ANGLE3 を使って三角形を描きます。
<![CDATA[
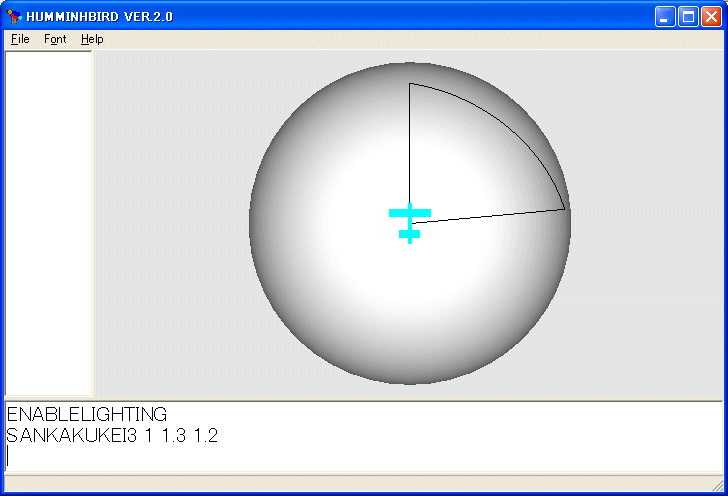
SETG_MODE 2
ENABLELIGHTING
SANKAKUKEI3 1 1.3 1.2
]]>
を実行します。
特別な場合として、一辺 :SIZE の正三角形を描くプログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI4 :SIZE
LOCAL :ANGLE :S
:S = :SIZE / RADIUS * 180 / PI
:ANGLE = ACOS ((COS :S)-(COS :S)*(COS :S))/((SIN :S)*(SIN :S))
REPEAT 3 [FD :SIZE RT 180-:ANGLE]
END
]]>
SANKAKUKEI4 1 を実行すれば、一辺 1 の正三角形を描きます。
球面三角形は三つの角を指定しても、角の余弦法則により、ただ一つに決まります。
球面三角形の内角の和は１８０度より大きいことに注意して下さい。
三つの内角 :A、 :B、 :C が与えられた
球面三角形を描くプログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI5 :A :B :C
LOCAL :SIDE1 :SIDE2 :SIDE3
:SIDE1 = ACOS ((COS :A)+(COS :B)*(COS :C))/((SIN :B)*(SIN :C))
:SIDE2 = ACOS ((COS :B)+(COS :C)*(COS :A))/((SIN :C)*(SIN :A))
:SIDE3 = ACOS ((COS :C)+(COS :A)*(COS :B))/((SIN :A)*(SIN :B))
:SIDE1 = :SIDE1 * PI / 180 * RADIUS
:SIDE2 = :SIDE2 * PI / 180 * RADIUS
:SIDE3 = :SIDE3 * PI / 180 * RADIUS
FD :SIDE3 RT 180 - :B FD :SIDE1 RT 180 - :C FD :SIDE2 RT 180 - :A
END
]]>
局所変数 :SIDE1、 :SIDE2、 :SIDE3 を宣言します｡角の余弦法則により、
対応する辺の大きさを計算します｡さらに、HUMMINGBIRD の球面の実際の辺の
長さを計算する。最後に三角形を描く。
特別な場合として、各内角が :A の正三角形を描くプログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI6 :A
LOCAL :S
:S = ACOS ((COS :A)+(COS :A)*(COS :A))/((SIN :A)*(SIN :A))
:S = :S * PI / 180 * RADIUS
REPEAT 3 [FD :S RT 180-:A]
END
]]>
SANKAKUKEI6 70 を実行すれば、各内角が７０度である正三角形を描きます。
次に平面双曲幾何を考えます。
双曲幾何学の正弦法則、余弦法則は次のようなものです。
△ABC は双曲三角形で、三辺の長さが a,b,c で、対応する内角が
α、β、γ の時､
正弦法則は
<![CDATA[
sinh a / sin α = sinh b / sin β = sinh c / sin γ
]]>
で、余弦法則は
<![CDATA[
cosh a = cosh b cosh c - sinh b sinh c cos α
cosh b = cosh c cosh a - sinh c sinh a cos β
cosh c = cosh a cosh b - sinh a sinh b cos γ
]]>
です。さらに､第二余弦法則
<![CDATA[
cosh a = (cos β cos γ + cos α) / (sin β sin γ)
cosh b = (cos γ cos α + cos β) / (sin γ sin α)
cosh c = (cos α cos β + cos γ) / (sin α sin β)
]]>
が成り立ちます。
余弦定理を使うと三つの辺の長さが与えられた三角形を描くプログラムは
次のようになります。
<![CDATA[
TO SANKAKUKEI7 :A :B :C
LOCAL :ALPHA :BETA :GAMMA
:ALPHA = ACOS ((COSH :B)*(COSH :C)-(COSH :A))/((SINH :B)*(SINH :C))
:BETA = ACOS ((COSH :C)*(COSH :A)-(COSH :B))/((SINH :C)*(SINH :A))
:GAMMA = ACOS ((COSH :A)*(COSH :B)-(COSH :C))/((SINH :A)*(SINH :B))
FD :A RT 180-:BETA FD :C RT 180-:ALPHA FD :B RT 180-:GAMMA
END
]]>
<![CDATA[
SETG_MODE 3
SANKAKUKEI7 1 3 2.5
]]>
を実行します。
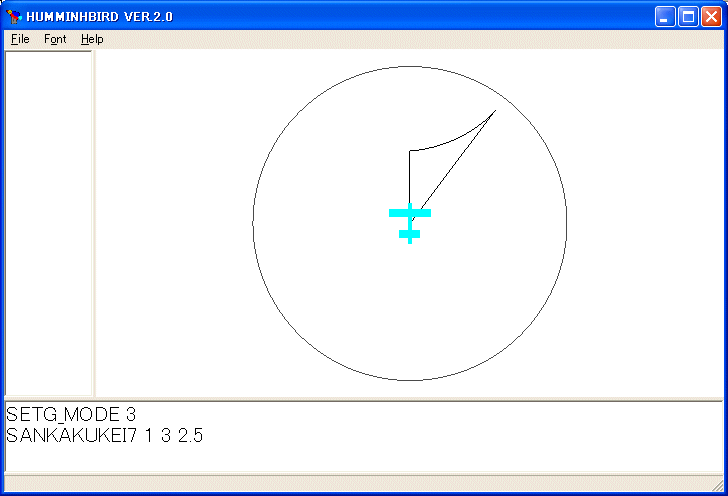
双曲幾何学でも、第二余弦法則により、三つの内角が与えられたとき、その内角を持つ三角形がただ一つ決まります。双曲三角形の内角の和は１８０度より小さいことに注意して下さい。
三つの内角 :ALPHA、 :BETA、 :GAMMA が与えられた
双曲三角形を描くプログラムは次のようになります。
<![CDATA[
TO SANKAKUKEI8 :ALPHA :BETA :GAMMA
LOCAL :A :B :C
:A = ACOSH ((COS :BETA)*(COS :GAMMA)+(COS :ALPHA))
/((SIN :BETA)*(SIN :GAMMA))
:B = ACOSH ((COS :GAMMA)*(COS :ALPHA)+(COS :BETA))
/((SIN :GAMMA)*(SIN :ALPHA))
:C = ACOSH ((COS :ALPHA)*(COS :BETA)+(COS :GAMMA))
/((SIN :ALPHA)*(SIN :BETA))
FD :A RT 180-:BETA FD :C RT 180-:ALPHA FD :B RT 180-:GAMMA
END
]]>
次に球面と双曲平面のタイル貼りを考察します。まず球面の場合を考察します。
４面角万華鏡を描くプログラムは角の余弦法則より
<![CDATA[
TO TETRA
LOCAL :SHORT :LONG
:SHORT = PI / 180 * ACOS 1 / SQRT 3
:LONG = PI / 180 * ACOS 1 / 3
PUSH
SETCOLOR 1 0 0 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 60
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:SHORT RT 60
SETCOLOR 1 0 0 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 60
PU FD :LONG PD RT 60
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT RT 60
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 60
PU BK :SHORT PD RT 90
SETCOLOR 1 0 0 FD :SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD :SHORT RT 90
PU POP PD
END
]]>
で与えられます。紙で模型を作って考えるといいです。
<![CDATA[
SETG_MODE 2
ENABLELIGHTING
TETRA
]]>
を実行すると次の図を描きます。
<![CDATA[
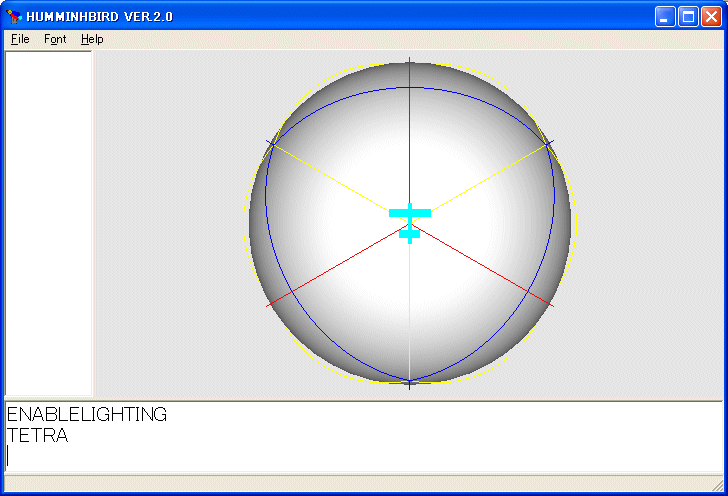
HS
]]>
を実行すると球面が消え次に用になります。
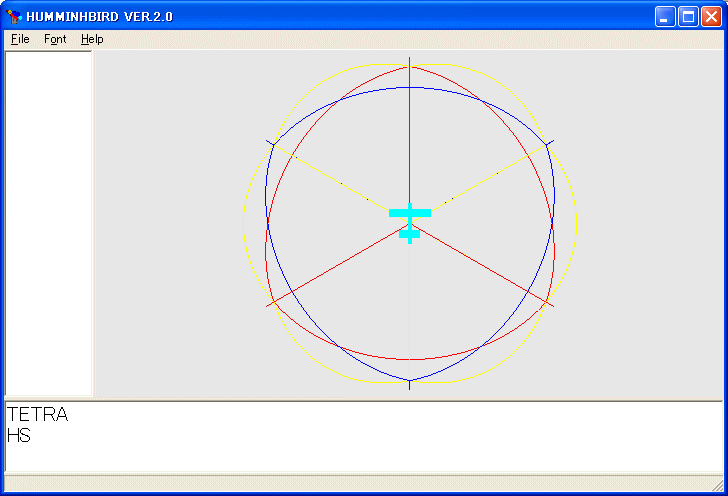
HS は HIDESPHERE の省略形です。
元に戻すには
<![CDATA[
SS
]]>
を実行します。SS は SHOWSPHERE の省略形です。
<![CDATA[
SURFACE 0.1
]]>
を実行すると線が面になり次のようになります。マウスで回転しています。
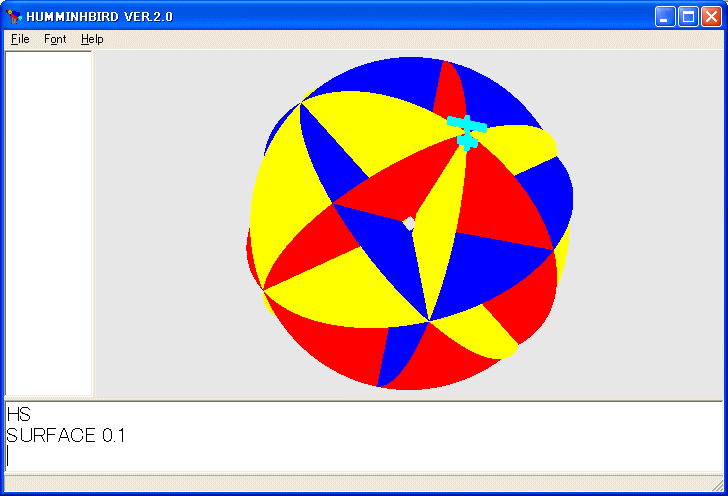
SURFACE は
<![CDATA[
SURFACE 式
]]>
の形式で使い、球面の表面から半径の式の値（0 から 1 まで）の割合の点まで結んだ面を描きます。元に戻すには
<![CDATA[
NONSURFACE
]]>
を実行します。
８面角万華鏡は次のプログラムで与えられます。
<![CDATA[
TO CUBE
LOCAL :SHORT :MIDDLE :LONG
:SHORT = PI / 180 * ACOS (SQRT 2)/(SQRT 3)
:MIDDLE = PI / 4
:LONG = PI / 180 * ACOS 1 / SQRT 3
PUSH
SETCOLOR 1 0 0 FD 2*PI RT 45
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD 2*:LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG RT 45
SETCOLOR 1 0 0 FD 2*PI RT 45
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD 2*:LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG RT 45
PU FD :MIDDLE PD RT 90
SETCOLOR 0 0 1 FD :SHORT SETCOLOR 1 1 0 FD 2*:LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD 2*:LONG
SETCOLOR 0 0 1 FD :SHORT RT 90
PU BK :MIDDLE PD RT 45
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD 2*:LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG RT 45
SETCOLOR 1 0 0 FD 2*PI RT 45
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD 2*:LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG RT 45
PU FD :MIDDLE PD RT 90
SETCOLOR 0 0 1 FD :SHORT SETCOLOR 1 1 0 FD 2*:LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD 2*:LONG
SETCOLOR 0 0 1 FD :SHORT
PU POP PD
END
]]>
<![CDATA[
CUBE
]]>
を実行すると次の図が描かれます。
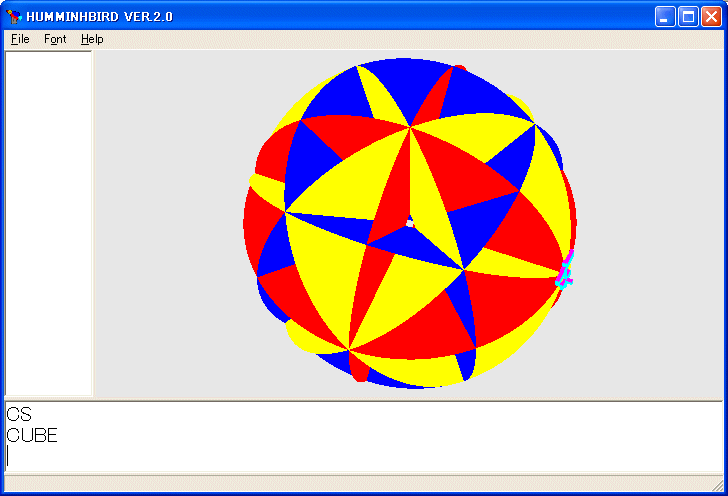
２０面角万華鏡を描くプログラムは次のようになります。
<![CDATA[
TO ICOSA
LOCAL :SHORT :MIDDLE :LONG
:SHORT = PI*20.9/180
:MIDDLE = PI*31.7166/180
:LONG = PI*37.3833/180
PUSH
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE RT 36
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 36
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE RT 36
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 36
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE RT 36
PU FD :MIDDLE PD RT 90
SETCOLOR 0 0 1 FD :SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD :SHORT RT 90
PU BK :MIDDLE PD RT 36
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE RT 36
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 36
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE RT 36
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG RT 36
PU FD :LONG PD RT 60
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT RT 60
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG RT 60
PU BK :SHORT PD RT 90
SETCOLOR 1 0 0 FD :MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD :MIDDLE RT 90
PU FD :SHORT PD RT 60
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG
SETCOLOR 0 0 1 FD 2*:SHORT SETCOLOR 1 1 0 FD :LONG
SETCOLOR 1 0 0 FD 2*:MIDDLE SETCOLOR 1 1 0 FD :LONG RT 60
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT
SETCOLOR 1 1 0 FD :LONG SETCOLOR 1 0 0 FD 2*:MIDDLE
SETCOLOR 1 1 0 FD :LONG SETCOLOR 0 0 1 FD 2*:SHORT RT 60
PU POP PD
END
]]>
<![CDATA[
ICOSA
]]>
を実行すると次の図が描かれます。
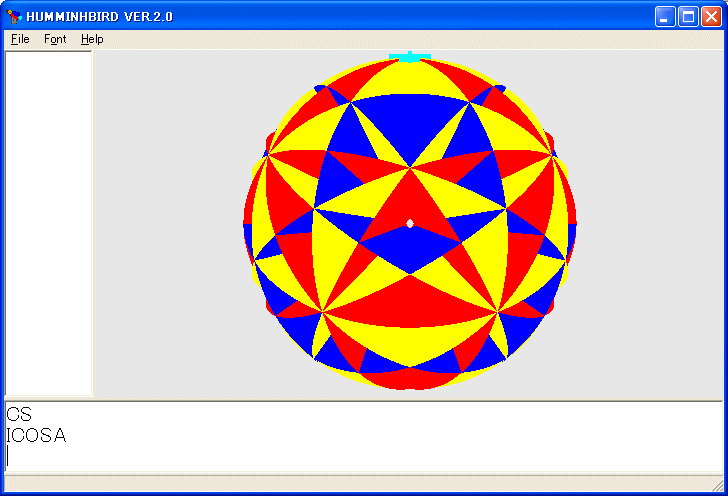
次に双曲平面のタイル貼りについて考えます。三角形は三つの角度を合計が 180 度より小さければ自由に選べますから、色々なタイル貼りが選べます。:N1 、 :N2 、 :N3 を 1/:N1 + 1/:N2 + 1/:N3 < 1/2 を満たす偶数として、:N を 0 以上の整数とするとき、少し長いですが次のプログラムで三角形のタイル貼りを描くことが出来ます。
<![CDATA[
TO TILING :N1 :N2 :N3 :N
LOCAL :ALPHA :BETA :GAMMA :A :B :C :I :K :SIND :TIND :IND :FLAG
:ALPHA = 360/:N1
:BETA = 360/:N2
:GAMMA = 360/:N3
:A = ACOSH((COS :BETA)*(COS :GAMMA)+(COS :ALPHA))/(SIN :BETA)/(SIN :GAMMA)
:B = ACOSH((COS :ALPHA)*(COS :GAMMA)+(COS :BETA))/(SIN :ALPHA)/(SIN :GAMMA)
:C = ACOSH((COS :ALPHA)*(COS :BETA)+(COS :GAMMA))/(SIN :ALPHA)/(SIN :BETA)
:LEN = 0
PUSH
FOR :I=0 TO :N1-1 [
IF :I % 2 == 0 [
FD :C RT 180-:BETA
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
FD :A RT 180-:GAMMA
FD :B RT 180-:ALPHA
][
FD :B RT 180-:GAMMA
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
FD :A RT 180-:BETA
FD :C RT 180-:ALPHA
]
RT :ALPHA
]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :N [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
:IND = GA :SIND*2
:FLAG = GA :SIND*2+1
IF :IND == 0 [
FOR :I=0 TO :N1-1 [
IF :I % 2 == :FLAG [
FD :C RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :A RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :B RT 180-:ALPHA
][
FD :B RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :A RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :C RT 180-:ALPHA
]
RT :ALPHA
]
]
IF :IND == 1 [
FOR :I=0 TO :N2-1 [
IF :I % 2 == :FLAG [
FD :A RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :B RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :C RT 180-:BETA
][
FD :C RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :B RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :A RT 180-:BETA
]
RT :BETA
]
]
IF :IND == 2 [
FOR :I=0 TO :N3-1 [
IF :I % 2 == :FLAG [
FD :B RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :C RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :A RT 180-:GAMMA
][
FD :A RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :C RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :B RT 180-:GAMMA
]
RT :GAMMA
]
]
:SIND = :SIND+1
]
:SIND = :TIND :TIND = :LEN
]
PU POP PD
END
]]>
<![CDATA[
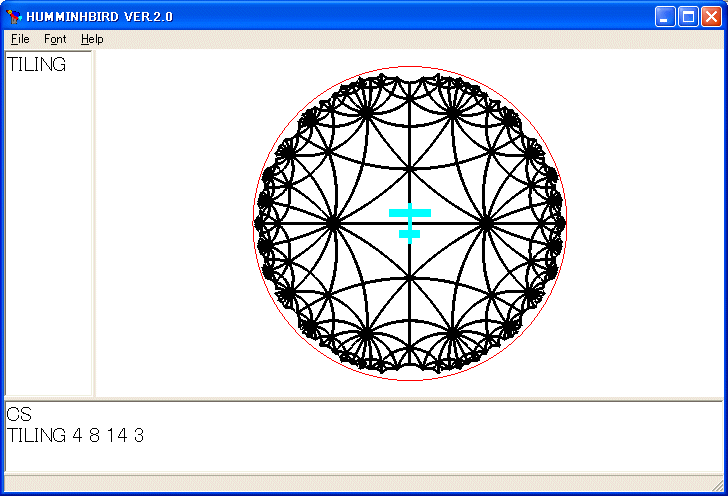
SETG_MODE 3
SETLINEWIDTH 3
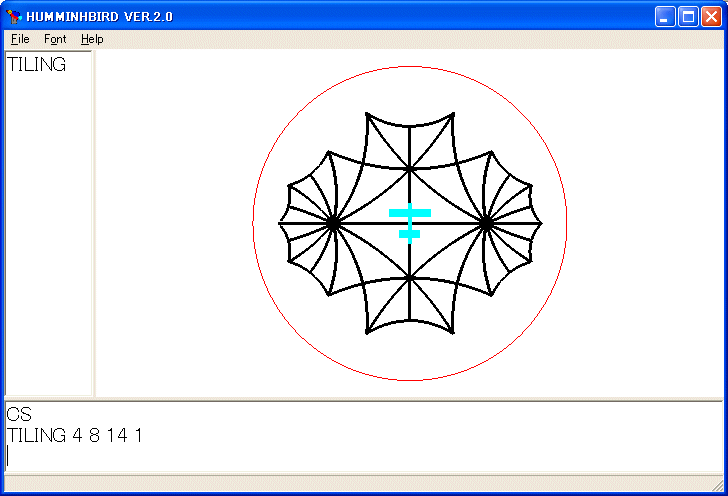
TILING 4 8 14 3
]]>
を実行しました。
上のプログラムの構造を調べてみます。まず
<![CDATA[
TILING 4 8 14 0
]]>
を実行します。
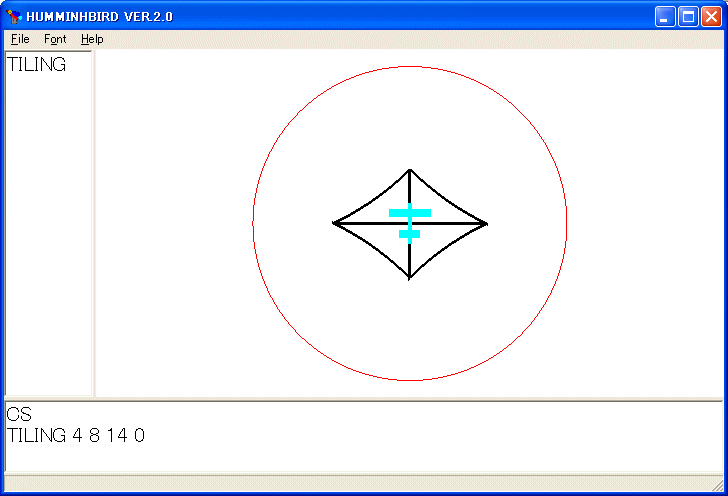
原点の周りに交互に三角形を描きました。
<![CDATA[
LOCAL :ALPHA :BETA :GAMMA :A :B :C :I :K :SIND :TIND :IND :FLAG
:ALPHA = 360/:N1
:BETA = 360/:N2
:GAMMA = 360/:N3
:A = ACOSH ((COS :BETA)*(COS :GAMMA)+
(COS :ALPHA))/(SIN :BETA)/(SIN :GAMMA)
:B = ACOSH ((COS :ALPHA)*(COS :GAMMA)+
(COS :BETA))/(SIN :ALPHA)/(SIN :GAMMA)
:C = ACOSH ((COS :ALPHA)*(COS :BETA)+
(COS :GAMMA))/(SIN :ALPHA)/(SIN :BETA)
:LEN = 0
PUSH
FOR :I=0 TO :N1-1 [
IF :I % 2 == 0 [
FD :C RT 180-:BETA
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
FD :A RT 180-:GAMMA
FD :B RT 180-:ALPHA
][
FD :B RT 180-:GAMMA
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
FD :A RT 180-:BETA
FD :C RT 180-:ALPHA
]
RT :ALPHA
]
]]>
の部分でそれをやっています。まず三角形のそれぞれの頂点の周りに三角形がいくつ描かれるべきかの数字が :N1 、 :N2 、 :N3 で与えられているので、それぞれの内角を :ALPHA 、 :BETA 、 :GAMMA にセットし、対応する辺の長さを第二余弦法則で計算し、:A 、 :B 、 :C にセットします。そして、三角形を表向きと裏向きと交互に :N1 個描きます。
次はその外側に三角形を交互に描く必要があります。その為に外側の頂点の位置と三角形をどのような順番で描くべきかの情報を保存しておき、その情報を使って三角形をそれぞれの頂点の周りに描きます。これをするために、飛行機の位置と向きを PUT 命令で配列に保存し、PA 命令で三角形の描き初めの頂点の番号と描く向きを記号化して保存しています。
プログラムの以下の部分で保存した情報を順次、GET 命令を使って飛行機の位置と向きを復元し、GA 命令で三角形の描き初めの頂点の番号と描く向きを記号化したものを取り出し、その頂点の周りに三角形を交互に描きます。さらに外側の三角形を描くために、配列を CONTAINED 命令を使って、データを保存していない新しい頂点に来たときは、その頂点に関する情報を保存します。この操作を指示されただけ繰り返しています。:N でこれを何段階までするかを制御しています。これはアルゴリズム的に見れば、描かれる図形をグラフとして見たとき、原点をルートとする横優先探索をしていることに当たります。これでずいぶん無駄な動きを省略することが可能になっています。
<![CDATA[
TILING 4 8 14 1
]]>
を実行すると次のようになります。
<![CDATA[
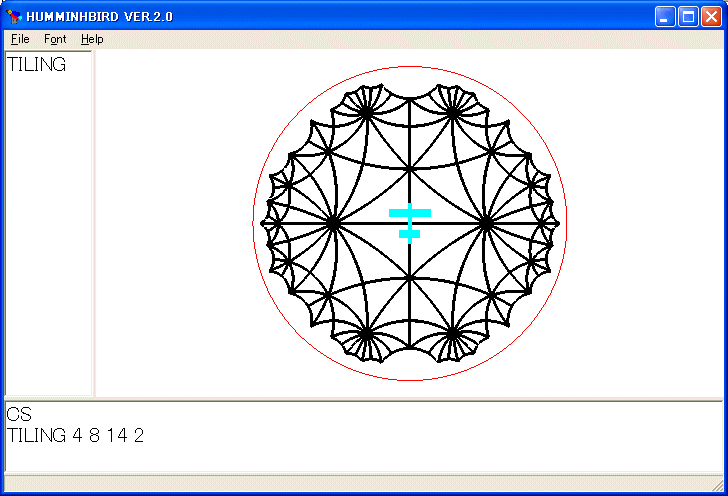
TILING 4 8 14 2
]]>
を実行すると次のようになります。
裏返しの三角形を塗ってみます。次のように修正します。
<![CDATA[
TO TILING2 :N1 :N2 :N3 :N
LOCAL :ALPHA :BETA :GAMMA :A :B :C :I :K :SIND :TIND :IND :FLAG
:ALPHA = 360/:N1
:BETA = 360/:N2
:GAMMA = 360/:N3
:A = ACOSH ((COS :BETA)*(COS :GAMMA)+(COS :ALPHA))/(SIN :BETA)/(SIN :GAMMA)
:B = ACOSH ((COS :ALPHA)*(COS :GAMMA)+(COS :BETA))/(SIN :ALPHA)/(SIN :GAMMA)
:C = ACOSH ((COS :ALPHA)*(COS :BETA)+(COS :GAMMA))/(SIN :ALPHA)/(SIN :BETA)
:LEN = 0
PUSH
FOR :I=0 TO :N1-1 [
IF :I % 2 == 0 [
FD :C RT 180-:BETA
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
FD :A RT 180-:GAMMA
FD :B RT 180-:ALPHA
][
POLYMODE
FD :B RT 180-:GAMMA
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
FD :A RT 180-:BETA
FD :C RT 180-:ALPHA
NONPOLYMODE
]
RT :ALPHA
]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :N [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
:IND = GA :SIND*2
:FLAG = GA :SIND*2+1
IF :IND == 0 [
FOR :I=0 TO :N1-1 [
IF :I % 2 == :FLAG [
FD :C RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :A RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :B RT 180-:ALPHA
][
POLYMODE
FD :B RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :A RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :C RT 180-:ALPHA
NONPOLYMODE
]
RT :ALPHA
]
]
IF :IND == 1 [
FOR :I=0 TO :N2-1 [
IF :I % 2 == :FLAG [
FD :A RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :B RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :C RT 180-:BETA
][
POLYMODE
FD :C RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :B RT 180-:GAMMA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 2 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :A RT 180-:BETA
NONPOLYMODE
]
RT :BETA
]
]
IF :IND == 2 [
FOR :I=0 TO :N3-1 [
IF :I % 2 == :FLAG [
FD :B RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :C RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 0 :LEN = :LEN+1
]
FD :A RT 180-:GAMMA
][
POLYMODE
FD :A RT 180-:BETA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 1 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :C RT 180-:ALPHA
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN PA :LEN*2 0 PA :LEN*2+1 1 :LEN = :LEN+1
]
FD :B RT 180-:GAMMA
NONPOLYMODE
]
RT :GAMMA
]
]
:SIND = :SIND+1
]
:SIND = :TIND :TIND = :LEN
]
PU POP PD
END
]]>
<![CDATA[
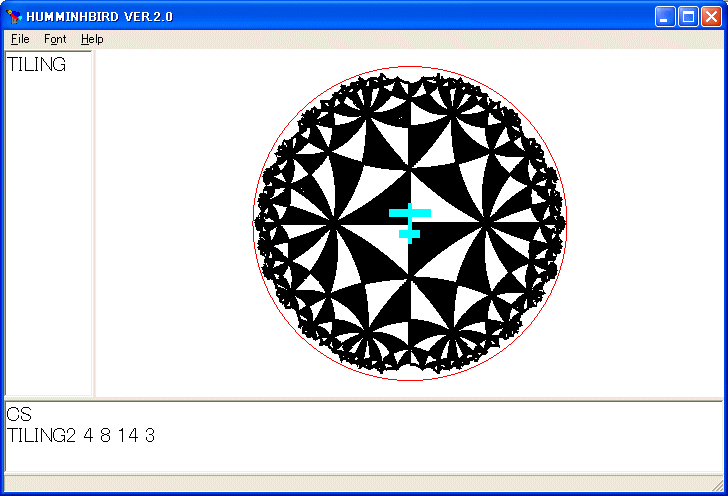
TILING2 4 8 14 3
]]>
を実行しました。プログラムの裏返しの三角形を描いている部分を POLYMODE と NONPOLYMODE で囲っているだけです。
次に正多角形のタイル張りを考えてみます。一つの内角 :ANGLE が与えられた正 :N 角形を描くプログラムを考察しました。このとき :ANGLE<(180(:N-2))/:N でなければなりません。双曲空間の正多角形の内角はかなり自由に変えることが出来るので、内角を調整すれば任意の正 :N 角形のタイル張りが可能です。ここでは正 :N 角形の各頂点の周りに :M 個正 :N 角形が並ぶタイル張りを考察します。ただし、$2/:M<(:N-2)/:N でなければなりません。プログラムは次のようになります。:L は何段階までタイル張りをするかの数字です。三角形の場合に比べ場合分けが必要ない文だけプログラムが簡単になりました。
<![CDATA[
TO POLYTILING :N :M :L
LOCAL :ANGLE :R :S :LEN :SIND :TIND
IF 2/:M >= (:N-2)/:N [STOP]
:ANGLE = 360 / :M
:S = ACOSH ((COS :ANGLE/2)*(COS :ANGLE/2)+(COS 360/:N))/((SIN :ANGLE/2)*(SIN :ANGLE/2))
:R = ACOSH ((COS :ANGLE/2)*(COS 360/:N)+(COS :ANGLE/2))/((SIN :ANGLE/2)*(SIN 360/:N))
PUSH PU FD :R RT 180 - :ANGLE/2 PD
:ANGLE = 180 - :ANGLE
:LEN = 0
REPEAT :N [FD :S RT :ANGLE PUT 1 :LEN :LEN = :LEN+1]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :L [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
REPEAT :M [
REPEAT :N [
FD :S RT :ANGLE
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN :LEN = :LEN+1
]
]
RT 180-:ANGLE
]
:SIND = :SIND+1
]
:SIND = :TIND
:TIND = :LEN
]
PU POP PD
END
]]>
<![CDATA[
POLYTILING 5 4 3
]]>
を実行しました。
<![CDATA[
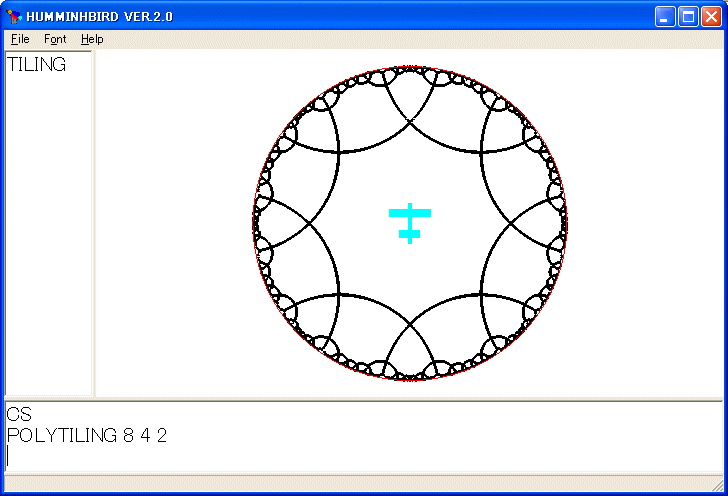
POLYTILING 8 4 2
]]>
を実行しました。
正 :N 角形を星形正 :N 角形に変更するために、STARPOLY を使います。STARTILING では、何回転しているかの数を :P で指示します。
<![CDATA[
TO STARPOLY :SIZE :N :M
LOCAL :X :ANGLE
:X = ACOSH (COSH :SIZE)*(COSH :SIZE)-(SINH :SIZE)*(SINH :SIZE)*(COS :M*360/:N)
:ANGLE = ACOS ((COSH :SIZE)*(COSH :X)-(COSH :SIZE))/((SINH :SIZE)*(SINH :X))
PUSH PU FD :SIZE RT 180-:ANGLE PD
:ANGLE = 180 - 2 * :ANGLE
REPEAT :N [ FD :X RT :ANGLE ]
PU POP PD
END
]]>
<![CDATA[
TO STARTILING :N :M :P :L
LOCAL :ANGLE :R :S :LEN :SIND :TIND
IF 2/:M >= (:N-2)/:N [STOP]
:ANGLE = 360 / :M
:S = ACOSH ((COS :ANGLE/2)*(COS :ANGLE/2)+(COS 360/:N))/((SIN :ANGLE/2)*(SIN :ANGLE/2))
:R = ACOSH ((COS :ANGLE/2)*(COS 360/:N)+(COS :ANGLE/2))/((SIN :ANGLE/2)*(SIN 360/:N))
STARPOLY :R :N :P
PUSH PU FD :R RT 180 - :ANGLE/2 PD
:ANGLE = 180 - :ANGLE
:LEN = 0
PU
REPEAT :N [FD :S RT :ANGLE PUT 1 :LEN :LEN = :LEN+1]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :L [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
REPEAT :M [
PUSH PU LT 90+:ANGLE/2 BK :R STARPOLY :R :N :P PU POP
REPEAT :N [
FD :S RT :ANGLE
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN :LEN = :LEN+1
]
]
RT 180-:ANGLE
]
:SIND = :SIND+1
]
:SIND = :TIND
:TIND = :LEN
]
PU POP PD
END
]]>
<![CDATA[
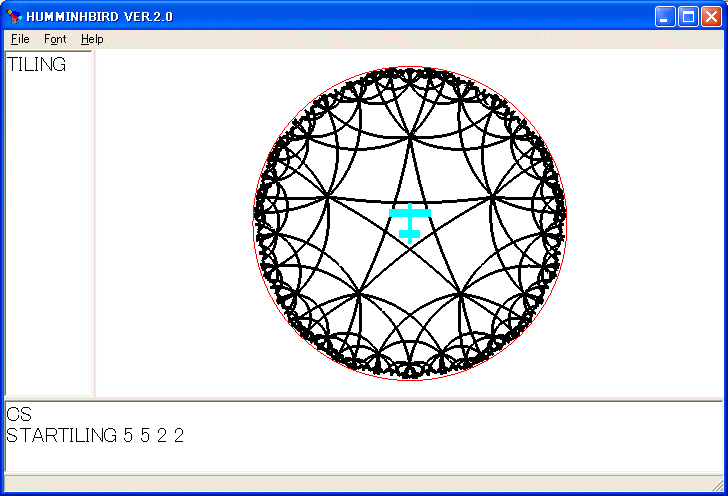
SETG_MODE 3
STARTILING 5 5 2 2
]]>
を実行しました。
星形正 :N 角形を塗りつぶすように上のプログラムを修正します。
<![CDATA[
TO STARFILL :SIZE :N :M
LOCAL :X :ANGLE
:X = ACOSH (COSH :SIZE)*(COSH :SIZE)-
(SINH :SIZE)*(SINH :SIZE)*(COS :M*360/:N)
:ANGLE = ACOS ((COSH :SIZE)*(COSH :X)-
(COSH :SIZE))/((SINH :SIZE)*(SINH :X))
PUSH PUSH TF PU2 POP2 PD2 PU FD :SIZE RT 180-:ANGLE PD
:ANGLE = 180 - 2 * :ANGLE
SYNCHRO SURFMODE
REPEAT :N [ FD :X RT :ANGLE ]
NONSYNCHRO NONSURFMODE
PU POP PD
END
]]>
<![CDATA[
TO STARFILLTILING :N :M :P :L
LOCAL :ANGLE :R :S :LEN :SIND :TIND :LEN2
IF 2/:M >= (:N-2)/:N [STOP]
:ANGLE = 360 / :M
:S = ACOSH ((COS :ANGLE/2)*(COS :ANGLE/2)+(COS 360/:N))/
((SIN :ANGLE/2)*(SIN :ANGLE/2))
:R = ACOSH ((COS :ANGLE/2)*(COS 360/:N)+(COS :ANGLE/2))/
((SIN :ANGLE/2)*(SIN 360/:N))
:LEN2 = 0
STARFILL :R :N :P PUT 2 :LEN2 :LEN2 = :LEN2+1
PUSH PU FD :R RT 180 - :ANGLE/2 PD
:ANGLE = 180 - :ANGLE
:LEN = 0
PU
REPEAT :N [FD :S RT :ANGLE PUT 1 :LEN :LEN = :LEN+1]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :L [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
REPEAT :M [
PUSH PU LT 90+:ANGLE/2 BK :R
IF CONTAINED 2 0 :LEN2 [
PU POP
][
PUT 2 :LEN2 :LEN2 = :LEN2+1 STARFILL :R :N :P PU POP
REPEAT :N [
FD :S RT :ANGLE
IF CONTAINED 1 0 :LEN [][
PUT 1 :LEN :LEN = :LEN+1
]
]
]
RT 180-:ANGLE
]
:SIND = :SIND+1
]
:SIND = :TIND
:TIND = :LEN
]
PU POP PD
END
]]>
<![CDATA[
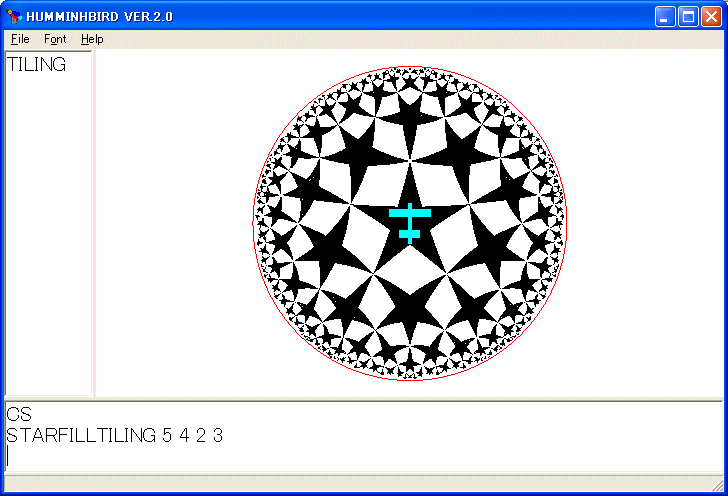
SETG_MODE 3
STARFILLTILING 5 4 2 3
]]>
を実行しました。上のプログラムではさらに、タートルを保存する二つ目の配列を使って、高速化しています。PUT2 命令と CONTAINED2 命令です。色々面白いタイル張りを考えて実行してみて下さい。
次に正多面体を描くプログラムを考えて見ます。
ユークリッド空間の正四面体のプログラムはすでに考えました。
正四面体の枠組みは次のプログラムで描けました。:A は枠組みの線の長さです。
<![CDATA[
TO TETRAFRAME :A
LOCAL :THETA
:THETA = ACOS -1/3
FD :A BK :A
DOWN :THETA
FD :A BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A BK :A
UP :THETA
END
]]>
線画の正四面体を描くプログラムは次のようなものでした。
<![CDATA[
TO TETRA :A
LOCAL :THETA
:THETA = ACOS -1/3
PU FD :A PUT 1 0 BK :A
DOWN :THETA
FD :A PUT 1 1 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 2 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 3 BK :A
UP :THETA
PUSH PUSH2
GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO
GET2 1 2 GET2 1 3 GET2 1 1
NONSYNCHRO
GET2 1 2 GET2 1 3 GET2 1 1
PU POP PD PU2 POP2 PD2
END
]]>
でした。
このプログラムは双曲空間でもそのまま通用します。
<![CDATA[
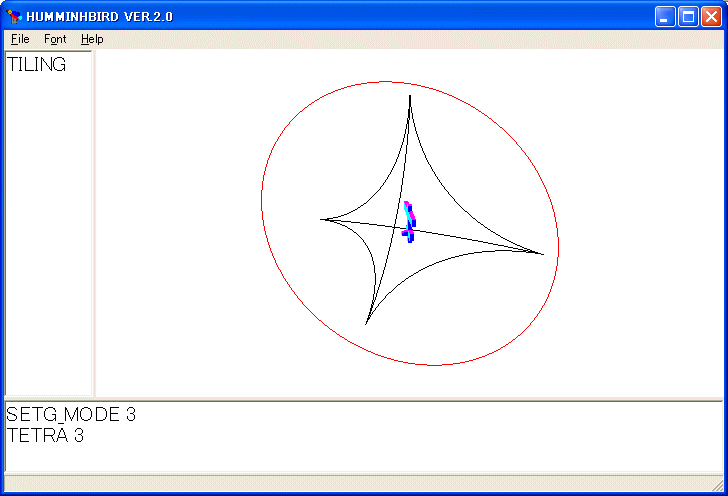
SETG_MODE 3
TETRA 3
]]>
を実行しました。マウスで画面を回転しています。
面を描くプログラムは次で与えられました。
<![CDATA[
TO TETRAFILL :A
LOCAL :THETA
:THETA = ACOS -1/3
FD :A PUT 1 0 BK :A
DOWN :THETA
FD :A PUT 1 1 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 2 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 3 BK :A
UP :THETA
PUSH PUSH2
PU GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET2 1 1
NONSYNCHRO NONSURFMODE
SETCOLOR RAND RAND RAND
POLYMODE
GET2 1 2 GET2 1 3 GET2 1 1
NONPOLYMODE
PU POP PD PU2 POP2 PD2
END
]]>
このプログラムは双曲空間でもそのまま通用します。
<![CDATA[
TETRAFILL 3
]]>
を実行すると次の図が描かれます。マウスで画面を回転しています。ENABLELIGHTING で照明を点けています。
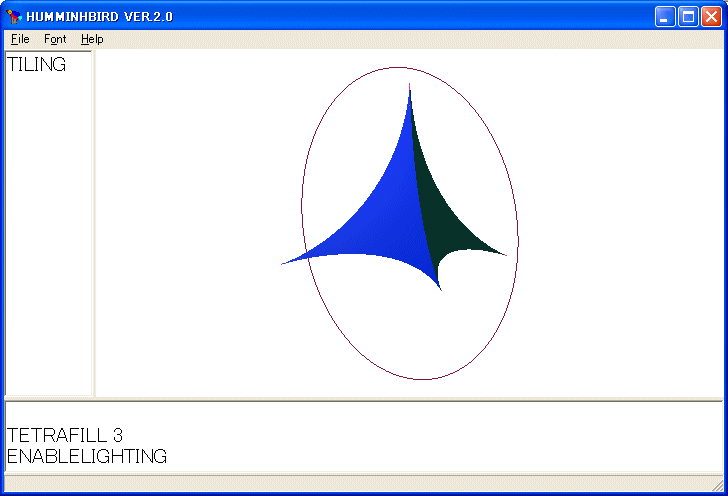
次に立方体を考えます。枠組みは次のプログラムで描けます。:A は枠組みの線の長さです。
<![CDATA[
TO CUBEFRAME :A
LOCAL :THETA
:THETA = ACOS 1/3
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA RT 120 UP 90
END
]]>
<![CDATA[
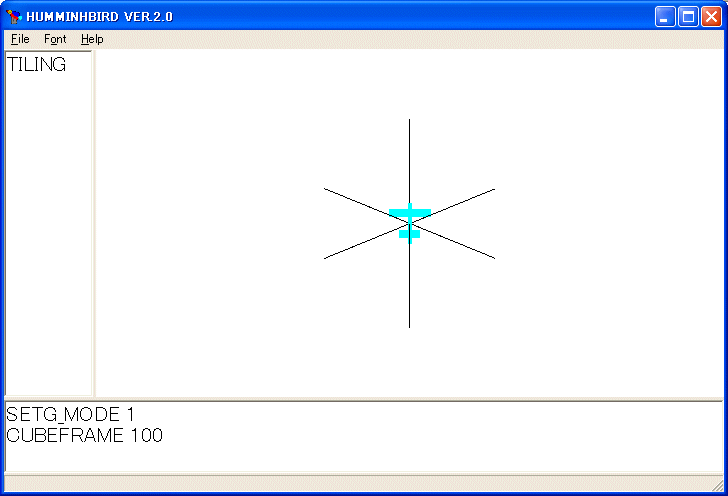
CUBEFRAME 100
]]>
を実行しました。
稜線を描いてみます。プログラムは以下のようになります。稜線を描くだけなら無駄な部分がありますが、面を描くことも考えて、すべての面に対して辺を描いています。
<![CDATA[
TO CUBE :A
LOCAL :THETA
:THETA = ACOS 1/3
PU
FD :A PUT 1 0 BK 2*:A PUT 1 6 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 5 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 2 FD :A
DOWN 90-:THETA RT 120 UP 90
PUSH PUSH2
PU GET 1 0 PD
GET 1 3 GET 1 2 GET 1 1 GET 1 0
GET 1 1 GET 1 5 GET 1 4 GET 1 0
GET 1 4 GET 1 7 GET 1 3 GET 1 0
PU GET 1 6 PD
GET 1 5 GET 1 1 GET 1 2 GET 1 6
GET 1 2 GET 1 3 GET 1 7 GET 1 6
GET 1 7 GET 1 4 GET 1 5 GET 1 6
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
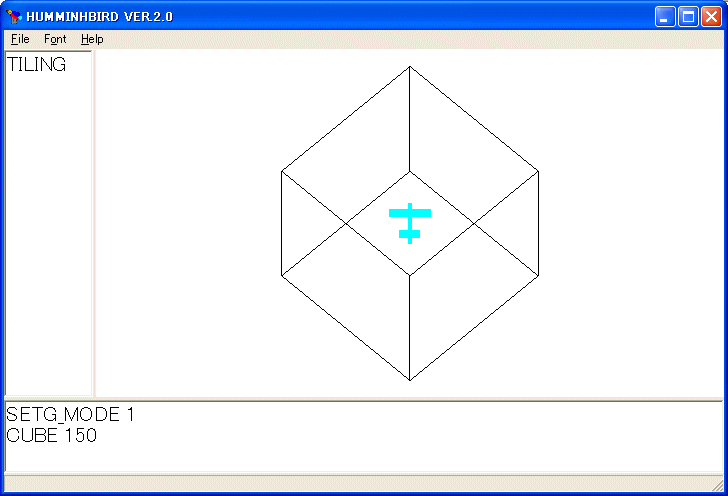
CUBE 150
]]>
を実行しました。双曲空間も同じプログラムで可能です。
<![CDATA[
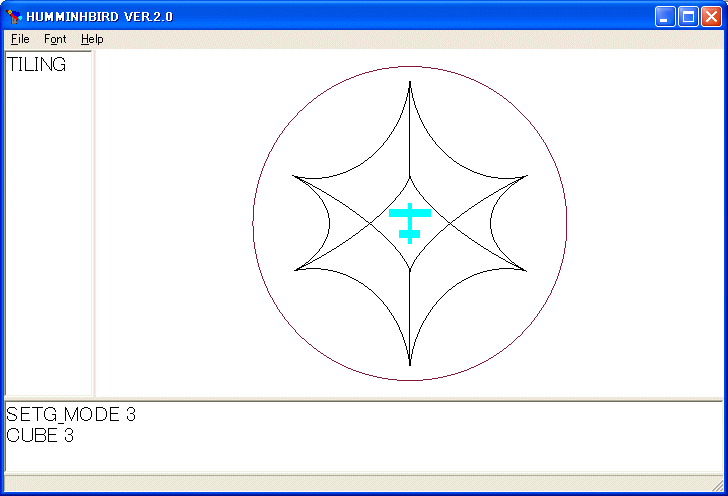
CUBE 3
]]>
を実行しました。面を描くには次のようにします。
<![CDATA[
TO CUBEFILL :A
LOCAL :THETA
:THETA = ACOS 1/3
FD :A PUT 1 0 BK 2*:A PUT 1 6 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 5 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 2 FD :A
DOWN 90-:THETA RT 120 UP 90
PUSH PUSH2
PU GET 1 0 PD
SETCOLOR 1 0 0 POLYMODE
GET 1 3 GET 1 2 GET 1 1 GET 1 0
NONPOLYMODE
SETCOLOR 0 1 0 POLYMODE
GET 1 1 GET 1 5 GET 1 4 GET 1 0
NONPOLYMODE
SETCOLOR 0 0 1 POLYMODE
GET 1 4 GET 1 7 GET 1 3 GET 1 0
NONPOLYMODE
PU GET 1 6 PD
SETCOLOR 1 1 0 POLYMODE
GET 1 5 GET 1 1 GET 1 2 GET 1 6
NONPOLYMODE
SETCOLOR 1 0 1 POLYMODE
GET 1 2 GET 1 3 GET 1 7 GET 1 6
NONPOLYMODE
SETCOLOR 0 1 1 POLYMODE
GET 1 7 GET 1 4 GET 1 5 GET 1 6
NONPOLYMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
CUBEFILL 150
]]>
を実行すると次の図が描かれます。
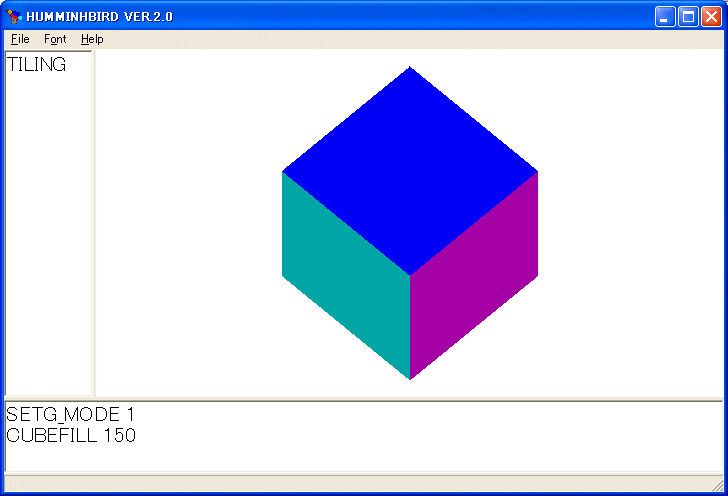
双曲空間も同じプログラムで可能です。
<![CDATA[
CUBEFILL 3
]]>
を実行すると次の図が描かれます。ENABLELIGHTING で照明を点けています。
次に正八面体を考えます。正八面体の枠組みは一番簡単です。次のようなプログラムで与えられます。
<![CDATA[
TO OCTAFRAME :A
FOR :I=0 TO 3 [FD :A BK :A RT 90]
UP 90 FD :A BK :A
UP 180 FD :A BK :A UP 90
END
]]>
<![CDATA[
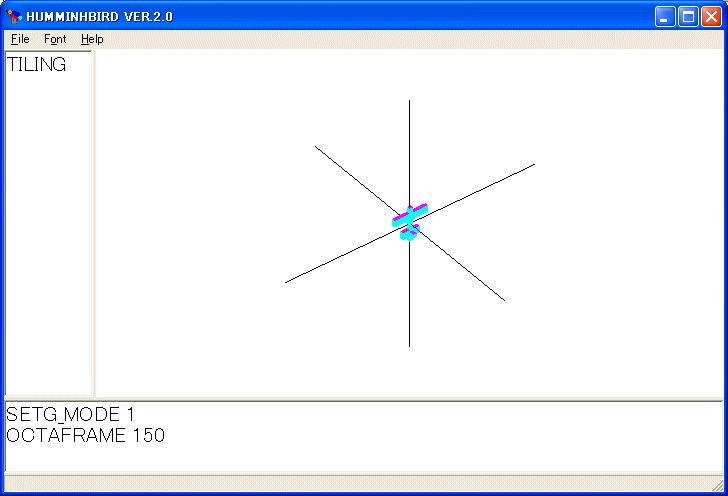
OCTAFRAME 150
]]>
を実行しました。マウスで回転しています。
稜線を描くには次のように修正します。
<![CDATA[
TO OCTA :A
PU
FOR :I=0 TO 3 [FD :A PUT 1 :I BK :A RT 90]
UP 90 FD :A PUT 1 4 BK :A
UP 180 FD :A PUT 1 5 BK :A UP 90
PUSH PUSH2
GET 1 4 PD PU2 GET2 1 0 PD2
SYNCHRO
GET2 1 1 GET2 1 2 GET2 1 3 GET2 1 0
NONSYNCHRO
GET2 1 1 GET2 1 2 GET2 1 3 GET2 1 0
PU GET 1 5 PD
SYNCHRO
GET2 1 3 GET2 1 2 GET2 1 1 GET2 1 0
NONSYNCHRO
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
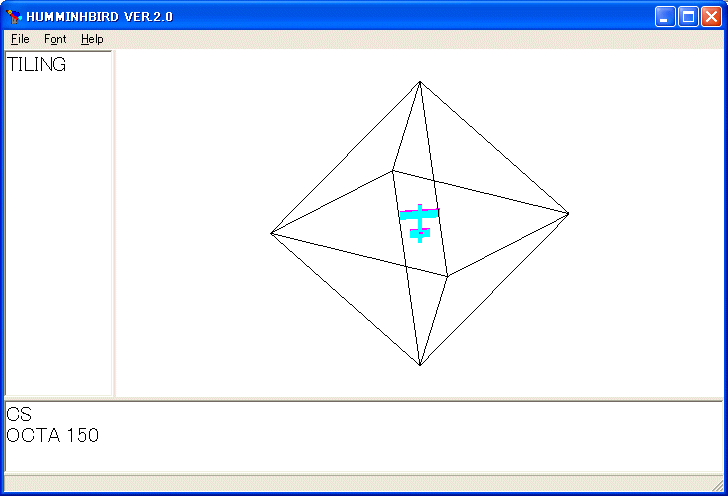
OCTA 150
]]>
を実行しました。マウスで回転しています。双曲空間も同じプログラムで可能です。
<![CDATA[
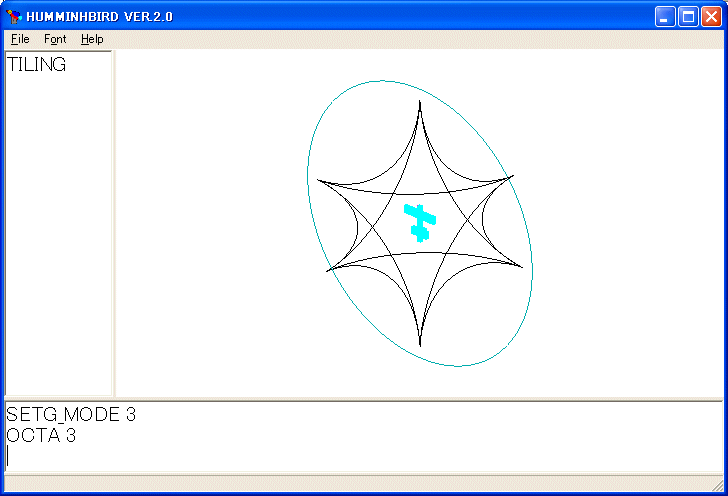
OCTA 3
]]>
を実行しました。マウスで回転しています。
面を描くには次のように修正します。
<![CDATA[
TO OCTAFILL :A
FOR :I=0 TO 3 [FD :A PUT 1 :I BK :A RT 90]
UP 90 FD :A PUT 1 4 BK :A
UP 180 FD :A PUT 1 5 BK :A UP 90
PUSH PUSH2
GET 1 4 PD PU2 GET2 1 0 PD2
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 1
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET2 1 0
NONSYNCHRO NONSURFMODE
PU GET 1 5 PD
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET2 1 1
SETCOLOR RAND RAND RAND GET2 1 0
NONSYNCHRO NONSURFMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
OCTAFILL 150
]]>
を実行すると次の図が描かれます。
<![CDATA[
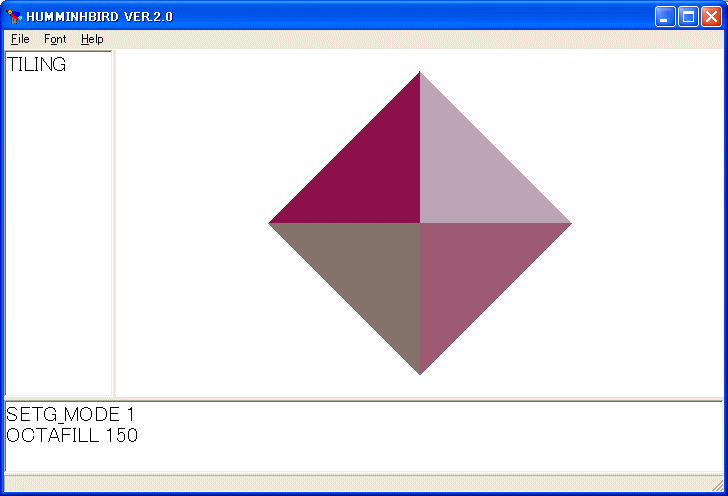
SETCOLOR RAND RAND RAND
]]>
と乱数を使って色を指定しています。実行するたびに色が変化します。
双曲空間も同じプログラムで可能です。
<![CDATA[
OCTAFILL 3
]]>
を実行すると次の図が描かれます。
ENABLELIGHTING で照明を点けています。
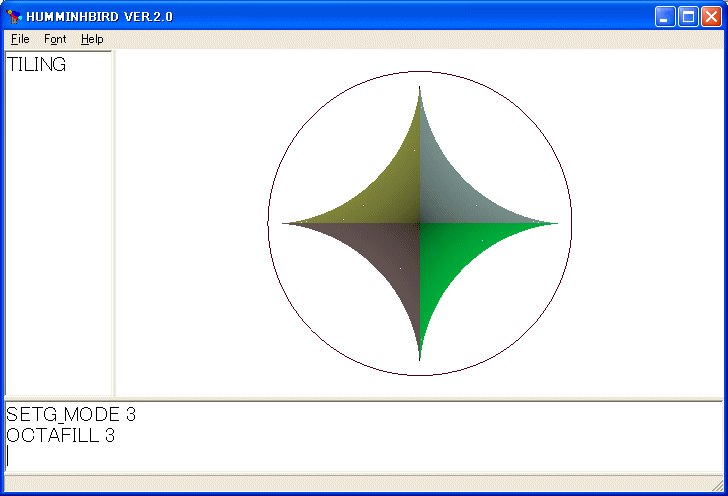
次に正十二面体を考察します。枠組みは次のプログラムで描けます。:A は枠組みの線の長さです。
<![CDATA[
TO DODECAFRAME :A
LOCAL :PHI :THETA
:PHI=ACOS (COT 36)*(COT 60)
:THETA=2*ACOS (COS 36)/(SIN 60)
DOWN :PHI
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90
END
]]>
<![CDATA[
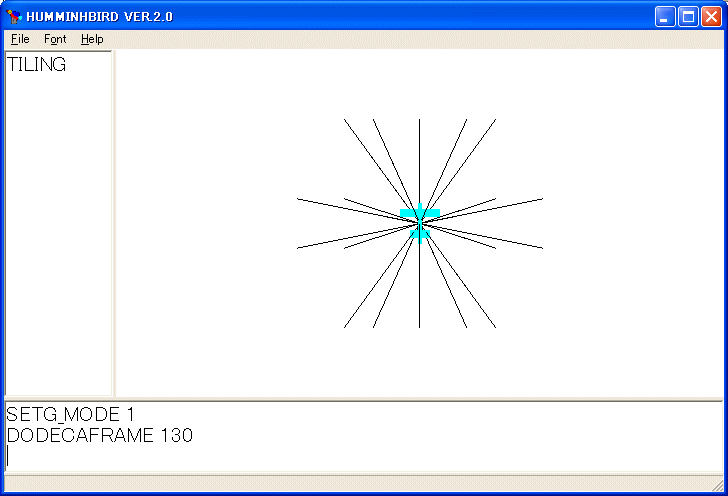
DODECAFRAME 130
]]>
を実行しました。
稜線を描くには次のように修正します。
<![CDATA[
TO DODECA :A
LOCAL :PHI :THETA
:PHI=ACOS (COT 36)*(COT 60)
:THETA=2*ACOS (COS 36)/(SIN 60)
PU
DOWN :PHI
FD :A PUT 1 0 BK 2*:A PUT 1 18 FD :A
DOWN :THETA
FD :A PUT 1 5 BK 2*:A PUT 1 12 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 1 BK 2*:A PUT 1 19 FD :A
DOWN :THETA
FD :A PUT 1 6 BK 2*:A PUT 1 13 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 2 BK 2*:A PUT 1 15 FD :A
DOWN :THETA
FD :A PUT 1 7 BK 2*:A PUT 1 14 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 3 BK 2*:A PUT 1 16 FD :A
DOWN :THETA
FD :A PUT 1 8 BK 2*:A PUT 1 10 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 4 BK 2*:A PUT 1 17 FD :A
DOWN :THETA
FD :A PUT 1 9 BK 2*:A PUT 1 11 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD
GET 1 1 GET 1 2 GET 1 3 GET 1 4 GET 1 0
GET 1 5 GET 1 10 GET 1 6 GET 1 1 GET 1 0
PU GET 1 1 PD
GET 1 6 GET 1 11 GET 1 7 GET 1 2 GET 1 1
PU GET 1 2 PD
GET 1 7 GET 1 12 GET 1 8 GET 1 3 GET 1 2
PU GET 1 3 PD
GET 1 8 GET 1 13 GET 1 9 GET 1 4 GET 1 3
PU GET 1 4 PD
GET 1 9 GET 1 14 GET 1 5 GET 1 0 GET 1 4
PU GET 1 5 PD
GET 1 14 GET 1 15 GET 1 16 GET 1 10 GET 1 5
PU GET 1 6 PD
GET 1 10 GET 1 16 GET 1 17 GET 1 11 GET 1 6
PU GET 1 7 PD
GET 1 11 GET 1 17 GET 1 18 GET 1 12 GET 1 7
PU GET 1 8 PD
GET 1 12 GET 1 18 GET 1 19 GET 1 13 GET 1 8
PU GET 1 9 PD
GET 1 13 GET 1 19 GET 1 15 GET 1 14 GET 1 9
PU GET 1 15 PD
GET 1 19 GET 1 18 GET 1 17 GET 1 16 GET 1 15
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
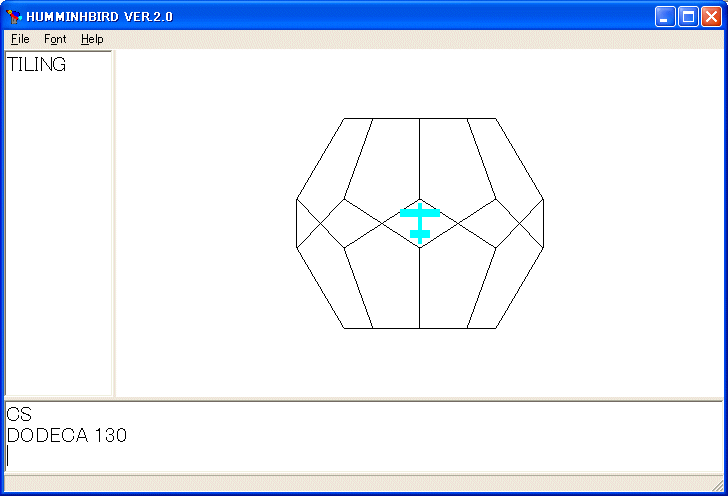
DODECA 130
]]>
を実行しました。マウスで回転しています。双曲空間も同じプログラムで可能です。
<![CDATA[
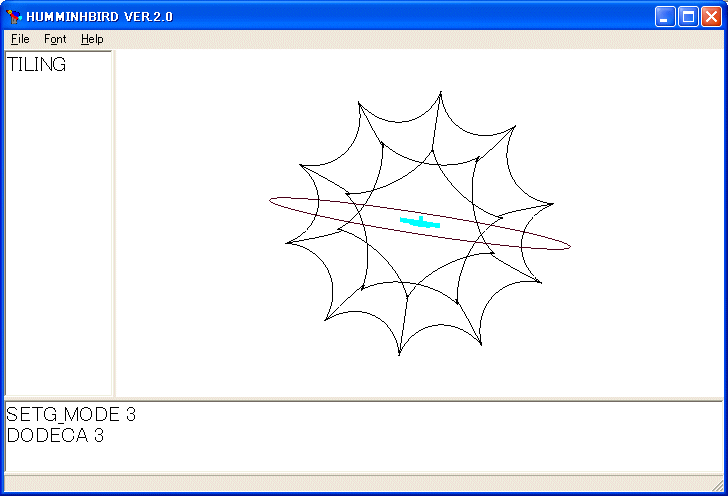
SETG_MODE 3
DODECA 3
]]>
を実行しました。マウスで回転しています。
面を描くには次のように修正します。
<![CDATA[
TO DODECAFILL :A
LOCAL :PHI :THETA
:PHI=ACOS (COT 36)*(COT 60)
:THETA=2*ACOS (COS 36)/(SIN 60)
PUSH PUSH2
DOWN :PHI
FD :A PUT 1 0 BK 2*:A PUT 1 18 FD :A
DOWN :THETA
FD :A PUT 1 5 BK 2*:A PUT 1 12 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 1 BK 2*:A PUT 1 19 FD :A
DOWN :THETA
FD :A PUT 1 6 BK 2*:A PUT 1 13 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 2 BK 2*:A PUT 1 15 FD :A
DOWN :THETA
FD :A PUT 1 7 BK 2*:A PUT 1 14 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 3 BK 2*:A PUT 1 16 FD :A
DOWN :THETA
FD :A PUT 1 8 BK 2*:A PUT 1 10 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 4 BK 2*:A PUT 1 17 FD :A
DOWN :THETA
FD :A PUT 1 9 BK 2*:A PUT 1 11 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90
PU GET 1 0 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 1 GET 1 2 GET 1 3 GET 1 4 GET 1 0
NONPOLYMODE
SETCOLOR RAND RAND RAND POLYMODE
GET 1 5 GET 1 10 GET 1 6 GET 1 1 GET 1 0
NONPOLYMODE
PU GET 1 1 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 6 GET 1 11 GET 1 7 GET 1 2 GET 1 1
NONPOLYMODE
PU GET 1 2 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 7 GET 1 12 GET 1 8 GET 1 3 GET 1 2
NONPOLYMODE
PU GET 1 3 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 8 GET 1 13 GET 1 9 GET 1 4 GET 1 3
NONPOLYMODE
PU GET 1 4 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 9 GET 1 14 GET 1 5 GET 1 0 GET 1 4
NONPOLYMODE
PU GET 1 5 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 14 GET 1 15 GET 1 16 GET 1 10 GET 1 5
NONPOLYMODE
PU GET 1 6 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 10 GET 1 16 GET 1 17 GET 1 11 GET 1 6
NONPOLYMODE
PU GET 1 7 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 11 GET 1 17 GET 1 18 GET 1 12 GET 1 7
NONPOLYMODE
PU GET 1 8 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 12 GET 1 18 GET 1 19 GET 1 13 GET 1 8
NONPOLYMODE
PU GET 1 9 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 13 GET 1 19 GET 1 15 GET 1 14 GET 1 9
NONPOLYMODE
PU GET 1 15 PD
SETCOLOR RAND RAND RAND POLYMODE
GET 1 19 GET 1 18 GET 1 17 GET 1 16 GET 1 15
NONPOLYMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
DODECAFILL 130
]]>
を実行すると次の図が描かれます。マウスで回転しています。
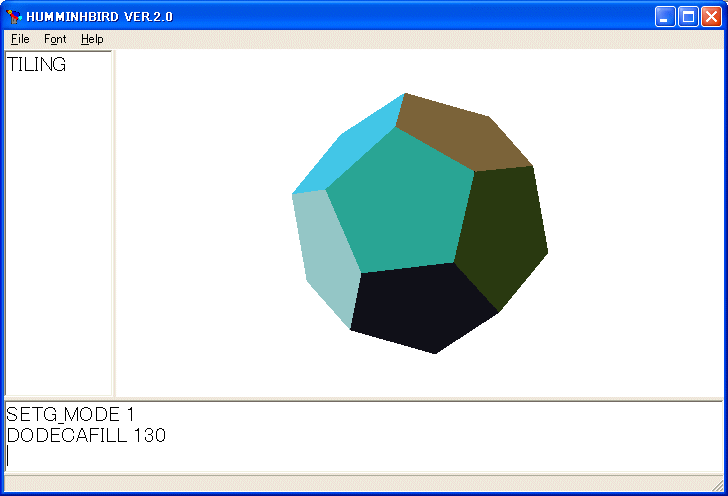
双曲空間も同じプログラムで可能です。
<![CDATA[
SETG_MODE 3 DODECAFILL 3 ENABLELIGHTING
]]>
を実行すると次の図が描かれます。
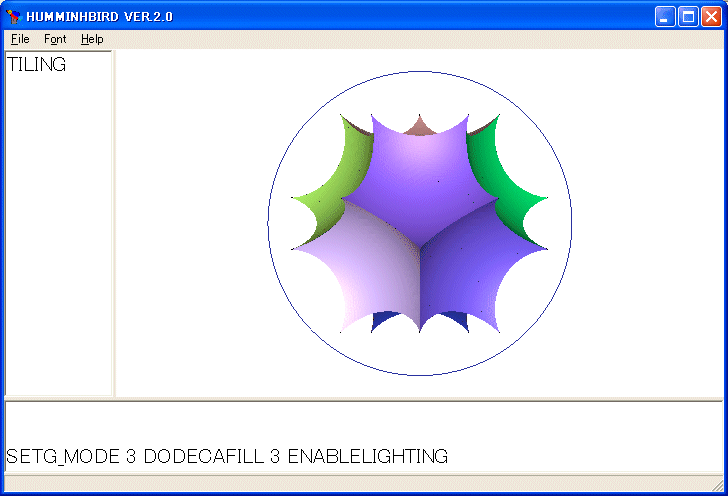
最後の正多面体は正二十面体です。枠組みは次のプログラムで与えられます。
<![CDATA[
TO ICOSAFRAME :A
LOCAL :THETA
:THETA = 2*ACOS (COS 60)/(SIN 36)
FD :A BK 2*:A FD :A
DOWN :THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A BK 2*:A FD :A
DOWN 90-:THETA LT 72 UP 90
END
]]>
<![CDATA[
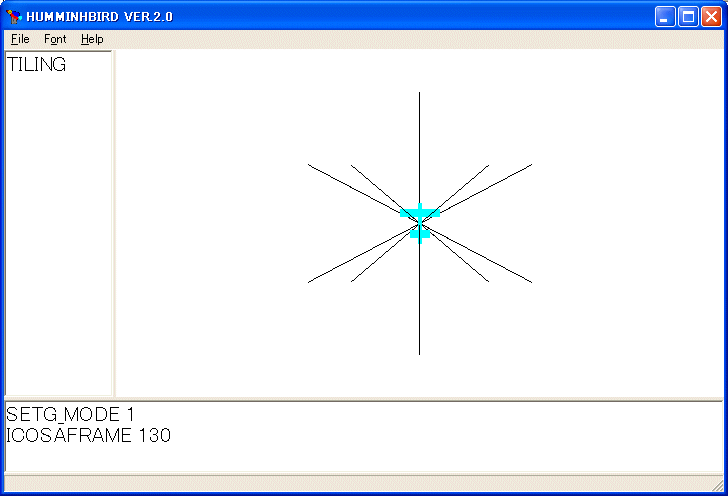
ICOSAFRAME 130
]]>
を実行しました。稜線を描くには次のように修正します。
<![CDATA[
TO ICOSA :A
LOCAL :THETA
:THETA = 2*ACOS (COS 60)/(SIN 36)
PU
FD :A PUT 1 0 BK 2*:A PUT 1 11 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 8 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 2 BK 2*:A PUT 1 9 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 10 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 6 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 5 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO
GET2 1 5 GET2 1 4 GET2 1 3 GET2 1 2 GET2 1 1
NONSYNCHRO
GET2 1 5 GET2 1 4 GET2 1 3 GET2 1 2 GET2 1 1
PU GET 1 6 PD
SYNCHRO
GET2 1 2 GET 1 7 GET2 1 2 GET2 1 3 GET 1 8 GET2 1 3 GET2 1 4
GET 1 9 GET2 1 4 GET2 1 5 GET 1 10 GET2 1 5 GET2 1 1 GET 1 6 GET2 1 1
NONSYNCHRO
PU GET 1 11 PD PU2 GET2 1 6 PD2
SYNCHRO
GET2 1 10 GET2 1 9 GET2 1 8 GET2 1 7 GET2 1 6
NONSYNCHRO
GET2 1 10 GET2 1 9 GET2 1 8 GET2 1 7 GET2 1 6
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
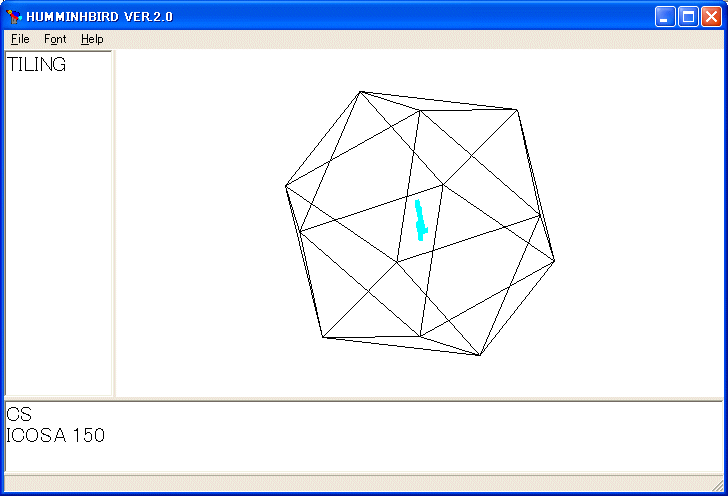
ICOSA 150
]]>
を実行しました。マウスで回転しています。双曲空間も同じプログラムで可能です。
<![CDATA[
ICOSA 3
]]>
を実行しました。マウスで回転しています。面を描くためには次のように修正します。
<![CDATA[
TO ICOSAFILL :A
LOCAL :THETA
:THETA = 2*ACOS (COS 60)/(SIN 36)
FD :A PUT 1 0 BK 2*:A PUT 1 11 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 8 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 2 BK 2*:A PUT 1 9 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 10 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 6 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 5 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 5
SETCOLOR RAND RAND RAND GET2 1 4
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET2 1 1
NONSYNCHRO NONSURFMODE
PU GET 1 6 PD
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET2 1 2
SETCOLOR RAND RAND RAND GET 1 7
SETCOLOR RAND RAND RAND GET2 1 3
SETCOLOR RAND RAND RAND GET 1 8
SETCOLOR RAND RAND RAND GET2 1 4
SETCOLOR RAND RAND RAND GET 1 9
SETCOLOR RAND RAND RAND GET2 1 5
SETCOLOR RAND RAND RAND GET 1 10
SETCOLOR RAND RAND RAND GET2 1 1
SETCOLOR RAND RAND RAND GET 1 6
NONSYNCHRO NONSURFMODE
PU2 GET2 1 11 PD2
SYNCHRO SURFMODE
SETCOLOR RAND RAND RAND GET 1 10
SETCOLOR RAND RAND RAND GET 1 9
SETCOLOR RAND RAND RAND GET 1 8
SETCOLOR RAND RAND RAND GET 1 7
SETCOLOR RAND RAND RAND GET 1 6
NONSYNCHRO NONSURFMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
ICOSAFILL 130
]]>
を実行すると次の図が描かれます。マウスで回転しています。
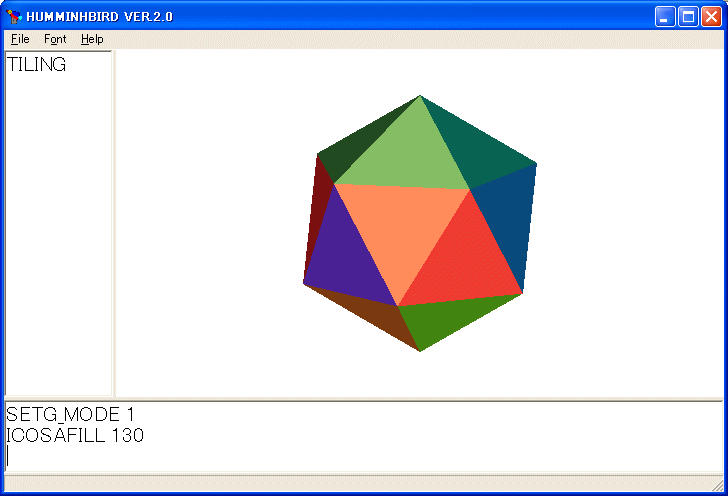
双曲空間も同じプログラムで可能です。
<![CDATA[
ICOSAFILL 3
]]>
を実行すると次の図が描かれます。
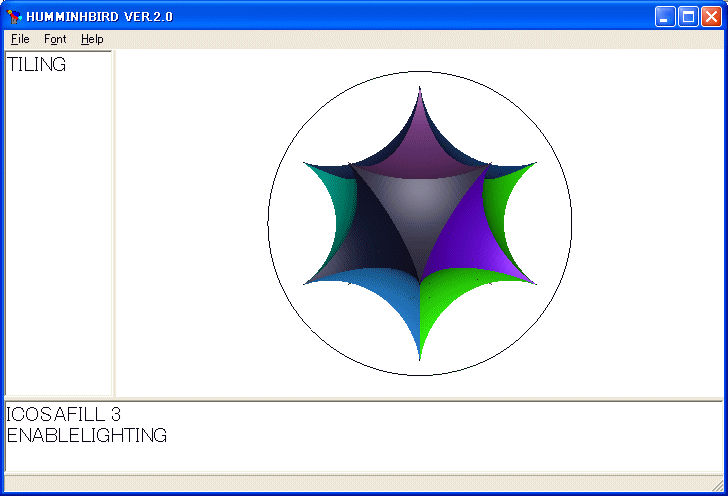
ICOSAFILL を次のように修正します。即ち、SETCOLOR RAND RAND RAND をすべて削除します。
<![CDATA[
TO ICOSAFILL :A
LOCAL :THETA
:THETA = 2*ACOS (COS 60)/(SIN 36)
FD :A PUT 1 0 BK 2*:A PUT 1 11 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 8 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 2 BK 2*:A PUT 1 9 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 10 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 6 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 5 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD PU2 GET2 1 1 PD2
SYNCHRO SURFMODE
GET2 1 5
GET2 1 4
GET2 1 3
GET2 1 2
GET2 1 1
NONSYNCHRO NONSURFMODE
PU GET 1 6 PD
SYNCHRO SURFMODE
GET2 1 2
GET 1 7
GET2 1 3
GET 1 8
GET2 1 4
GET 1 9
GET2 1 5
GET 1 10
GET2 1 1
GET 1 6
NONSYNCHRO NONSURFMODE
PU2 GET2 1 11 PD2
SYNCHRO SURFMODE
GET 1 10
GET 1 9
GET 1 8
GET 1 7
GET 1 6
NONSYNCHRO NONSURFMODE
PU POP PD PU2 POP2 PD2
END
]]>
<![CDATA[
SETG_MODE 3
SETCOLOR 1 1 1
ICOSAFILL 3
]]>
を事項すると次のような図を描きます。
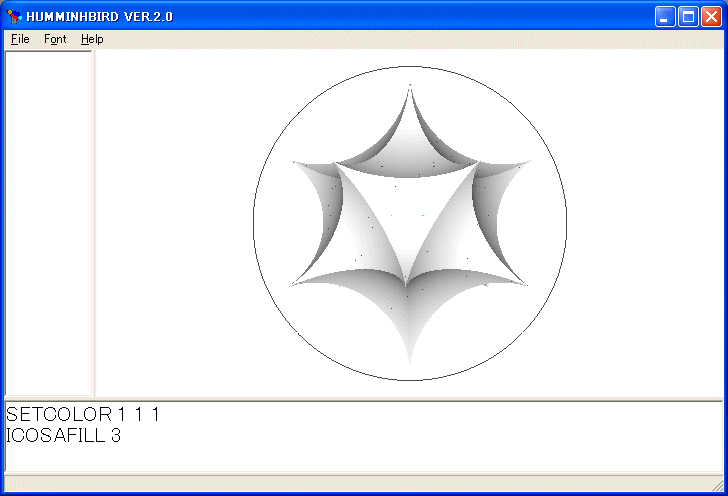
主な使い方は紹介しました。残りの機能が知りたいときは、ヘルプを見て下さい。面白いプログラムが出来たら、作者にも教えてください。osamu@kochi-u.ac.jp までメールをいただければ幸いです。バグ情報やこんな機能があれば非常に便利だというものを思いつかれたら同様に教えてください。では、三次元 LOGO の世界をお楽しみください。