■ サンプルプログラムを幾つか与えます。
平面図形のサンプルは Harold Abelson and Andrea diSessa : TURTLE GEOMETRY (The Computer as a Medium for Exploring Mathmatics), The MIT Press にたくさんあります。この本には生物の動きのシミュレーションのプログラムなどおもしろいものがたくさん載っています。翻訳が出る話もあったみたいですが、中止になったみたいです。英語の本ですが易しいですから、LOGO に興味が出てきたなら是非お読み下さい。かってはLOGO は子供向けの教育言語として、またKITEには備わっていませんが、LIST処理を使った人工知能のための言語として人気があり、古い本で良ければ平面 LOGO の本は沢山出版されています。
KITE は 空間 LOGO ですから、ここからは三次元のプログラミングを考えてみましょう。プログラムを理解するのはちょっと難しいかも分かりません。球面幾何学の公式を使います。正四面体を描く手続きを一般化してみます。四面体の模型を作って考えると良いです。
例:
TO TETRA :A :B :C :D :E :F
FD :A
RT 180 - ACOS (:A*:A+:B*:B-:C*:C)/(2*:A*:B)
FD :B
RT 180 - ACOS (:B*:B+:C*:C-:A*:A)/(2*:B*:C)
FD :C
RT 180 - ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
LOCAL :X :Y :Z
:X = ACOS (:C*:C+:A*:A-:B*:B)/(2*:C*:A)
:Y = ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
:Z = ACOS (:D*:D+:C*:C-:F*:F)/(2*:D*:C)
YAW 180 - ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
FD :A
LT 180 - ACOS (:A*:A+:E*:E-:D*:D)/(2*:A*:E)
FD :E
LT 180 - ACOS (:E*:E+:D*:D-:A*:A)/(2*:E*:D)
FD :D
LT 180 - ACOS (:D*:D+:A*:A-:E*:E)/(2*:D*:A)
LT :Y
YAW 180 - ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
FD :D
LT 180 - ACOS (:D*:D+:F*:F-:C*:C)/(2*:D*:F)
FD :F
LT 180 - ACOS (:F*:F+:C*:C-:D*:D)/(2*:F*:C)
FD :C
LT 180 - ACOS (:C*:C+:D*:D-:F*:F)/(2*:C*:D)
YAW -180 + ACOS ((COS :X)-(COS :Y)*(COS :Z))/((SIN :Y)*(SIN :Z))
RT :Y
YAW -180 + ACOS ((COS :Z)-(COS :X)*(COS :Y))/((SIN :X)*(SIN :Y))
END
これは四面体 ABCD の各辺 AB, BC, CA, AD, BD, CD の長さを与えたとき、その条件を満たす四面体を描くプログラムです。
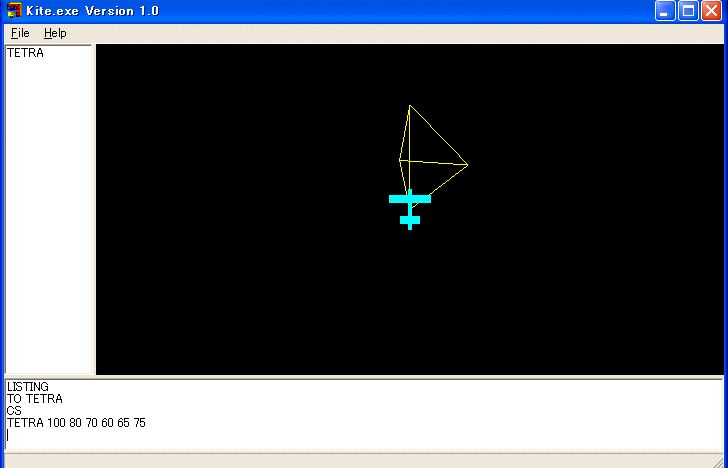
例:
正四面体を一般化します。
TO KAKUSUI :N :X
IF (:N < 3) || (:N > 5) [STOP]
LOCAL :Y :H
:Y = :X / 2 / SIN 180 / :N
:H = SQRT :X*:X-:Y*:Y
PU FD :H PD
PU2 DOWN2 90 FD2 :Y RT2 90 + 180 / :N PD2
ST2
REPEAT :N [FD2 :X RT2 360 / :N]
SYNCHRO
REPEAT :N [FD2 :X RT2 360 / :N]
NONSYNCHRO
PU BK :H PD
PU2 LT2 90 + 180 / :N FD2 -:Y UP2 90 PD2 HT2
END
は正三角錐(正四面体)、正四角錐、正五角錐を描く手続きです。
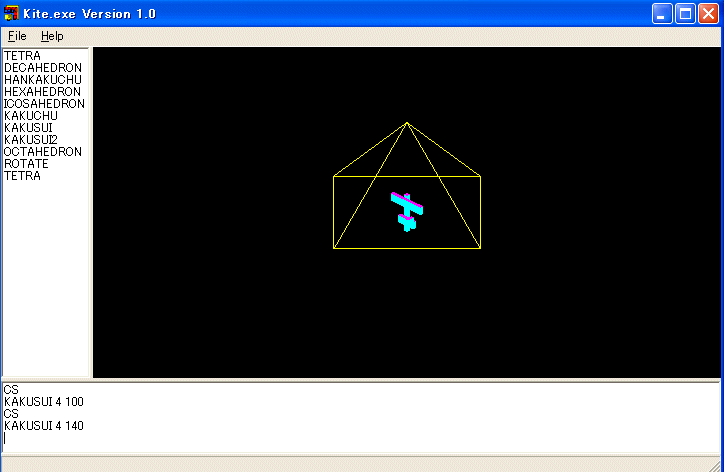
少し修正して、次のような手続きも正二十面体のために作っておきます。
TO KAKUSUI2 :N :X
IF (:N < 3) || (:N > 5) [STOP]
LOCAL :Y :H
:Y = :X / 2 / SIN 180 / :N
:H = SQRT :X*:X-:Y*:Y
PU FD :H PD
PU2 DOWN2 90 RT2 180 / :N FD2 :Y RT2 90 + 180 / :N PD2
ST2
REPEAT :N [FD2 :X RT2 360 / :N]
SYNCHRO
REPEAT :N [FD2 :X RT2 360 / :N]
NONSYNCHRO
PU BK :H PD
PU2 LT2 90 + 180 / :N FD2 -:Y LT2 180 / :N UP2 90 PD2 HT2
END
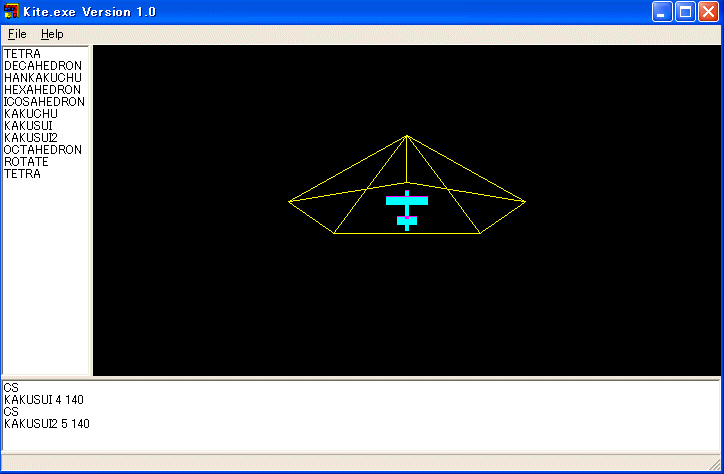
例:
KAKUSUI を使えば、正八面体を描く手続きが作れます。
TO OCTAHEDRON :X
KAKUSUI 4 :X
RT 180 RT2 180
KAKUSUI 4 :X
RT 180 RT2 180
END
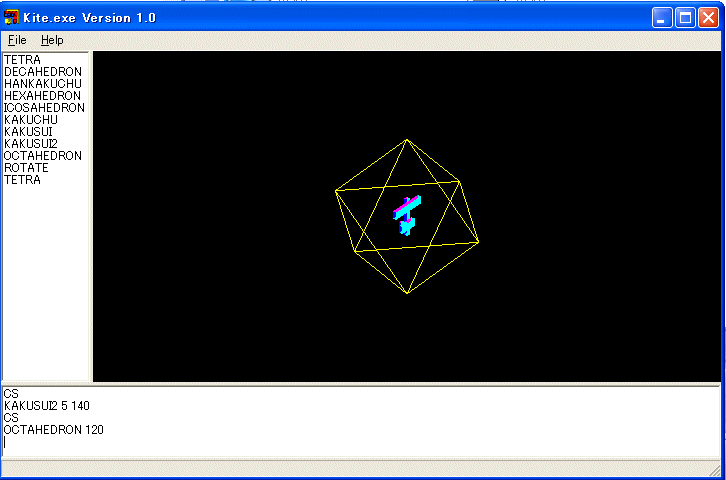
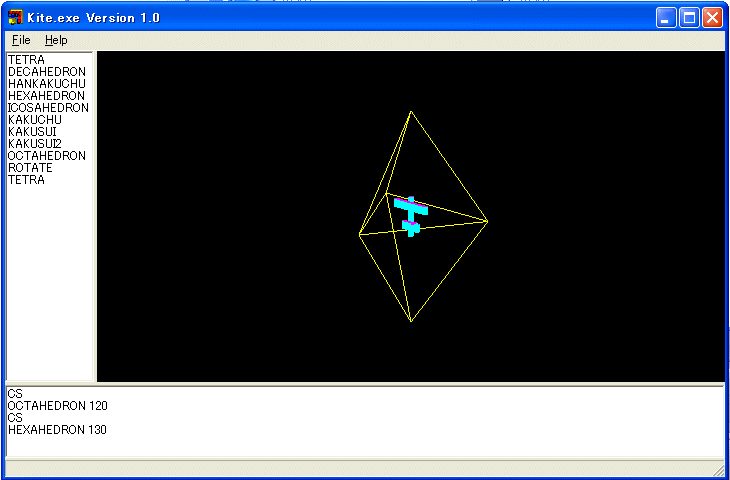
さらに、デルタ多面体の六面体と十面体です。
TO HEXAHEDRON :X
KAKUSUI 3 :X
RT 180 RT2 180
KAKUSUI 3 :X
RT 180 RT2 180
END
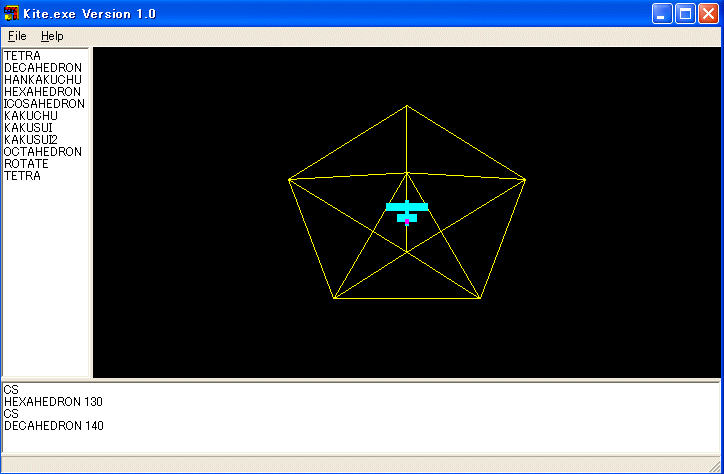
TO DECAHEDRON :X
KAKUSUI 5 :X
RT 180 RT2 180
KAKUSUI 5 :X
RT 180 RT2 180
END
例:
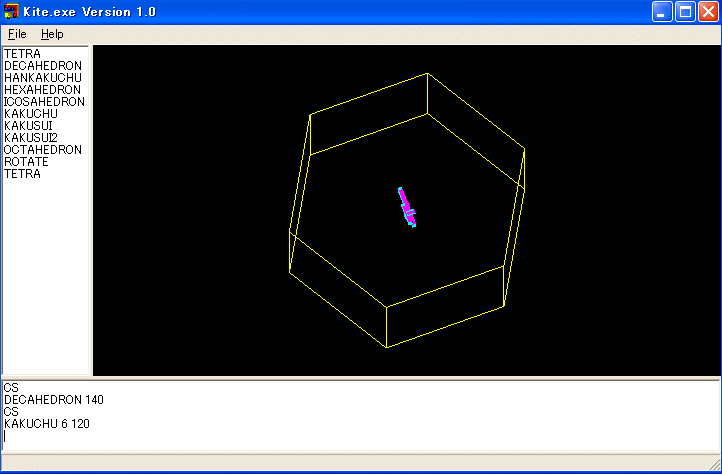
正多角柱を描く手続きです。
TO KAKUCHU :N :X
LOCAL :Y :H
:Y = :X / 2 / SIN 180 / :N
:H = :X / 2
PU FD :H DOWN 90 FD :Y RT 90+180/:N PD
REPEAT :N [FD :X RT 360 / :N]
PU2 FD2 -:H DOWN2 90 FD2 :Y RT2 90+180/:N PD2
ST2
REPEAT :N [FD2 :X RT2 360 / :N]
SYNCHRO
REPEAT :N [FD :X RT 360 / :N FD2 :X RT2 360 / :N]
NONSYNCHRO
PU LT 90+180/:N FD -:Y UP 90 BK :H PD
PU2 LT2 90+180/:N FD2 -:Y UP2 90 BK2 -:H PD2
HT2
END
例:
正多角反柱を描く手続きです。
TO HANKAKUCHU :N :X
LOCAL :Y :Z :H
:Y = :X / 2 / SIN 180 / :N
:Z = 2 * :Y * SIN 90 / :N
:H = (SQRT :X*:X - :Z*:Z) / 2
PU FD :H DOWN 90 FD :Y RT 90+180/:N PD
REPEAT :N [FD :X RT 360 / :N]
PU2 FD2 -:H DOWN2 90 RT2 180/:N FD2 :Y RT2 90+180/:N PD2
ST2
REPEAT :N [FD2 :X RT2 360 / :N]
SYNCHRO
REPEAT :N [FD :X RT 360 / :N FD2 0 FD2 :X RT2 360 / :N]
NONSYNCHRO
PU LT 90+180/:N FD -:Y UP 90 BK :H PD
PU2 LT2 90+180/:N FD2 -:Y LT2 180/:N UP2 90 BK2 -:H PD2
HT2
END
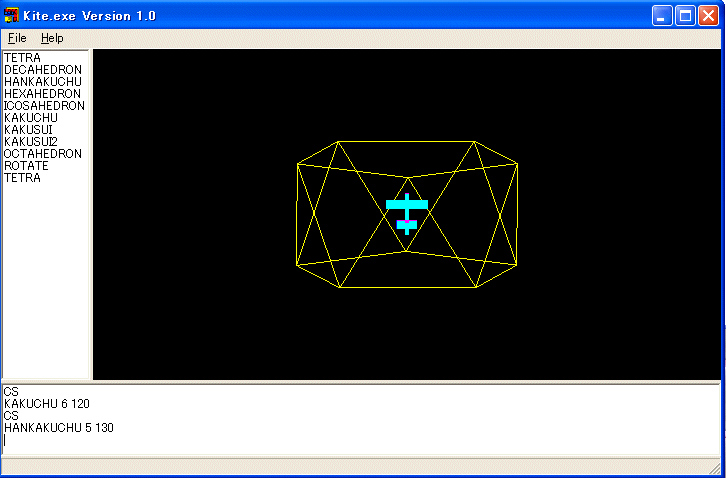
例: KAKUSUI, KAKUSUI2, HANKAKUCHU を使えば、正二十面体を描く手続きが定義できます。正五角反柱の上下に正五角錐を載せます。
TO ICOSAHEDRON :X
LOCAL :Y :Z :H
:Y = :X / 2 / SIN 180 / 5
:Z = 2 * :Y * SIN 90 / 5
:H = (SQRT :X*:X - :Z*:Z) / 2
PU FD :H PD
PU2 FD2 :H PD2
KAKUSUI 5 :X
PU FD -:H PD
PU2 FD2 -:H PD2
HANKAKUCHU 5 :X
PU FD -:H RT 180 PD
PU2 FD2 -:H RT2 180 PD2
KAKUSUI2 5 :X
PU RT 180 FD :H PD
PU2 RT2 180 FD2 :H PD2
END
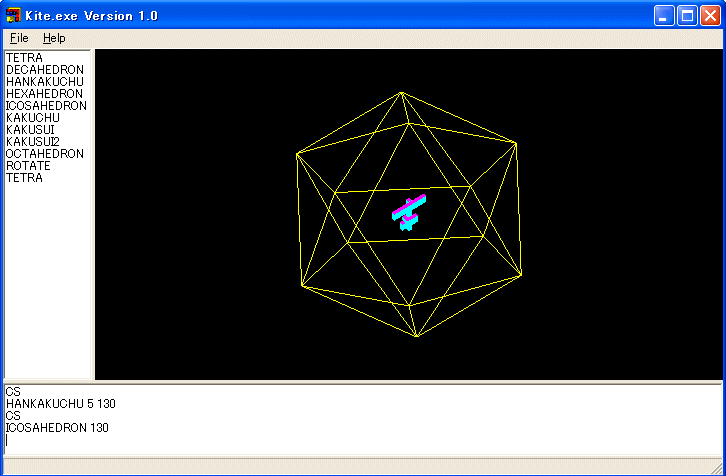
例:最後は正十二面体です。参考書は一松信著「正多面体を解く」東海大学出版会です。内接球の半径と外接球の半径と二面角の情報が必要です。
TO DODECA :X
LOCAL :Z :PHI :D :R :H :Y
:Z = ((SIN 180/5)*(SIN 180/5)-2*(COS 180/3)*(COS 180/3))/((SIN 180/5)*(SIN 180/5))
:PHI = ACOS :Z
:D = SQRT 1 - (COS 180/5)*(COS 180/5)-(COS 180/3)*(COS 180/3)
:H = :X / (TAN 180/5)*(COS 180/3)/(2*:D)
:R = :X * (SIN 180/3)/(2*:D)
:Y = SQRT (:R*:R - :H*:H)
PUSH
PU FD :H DOWN 90 FD :Y RT 126 PD
REPEAT 5 [FD :X RT 72]
YAW -180 +:PHI LT 108
REPEAT 5 [
REPEAT 4 [FD :X RT 72]
RT 108 YAW 180 - :PHI
]
PU POP PD
PUSH
PU FD -:H DOWN 90 RT 36 FD :Y RT 126 PD
REPEAT 5 [FD :X RT 72]
YAW 180 -:PHI LT 108
REPEAT 5 [
REPEAT 4 [FD :X RT 72]
RT 108 YAW -180 + :PHI
]
PU POP PD
END
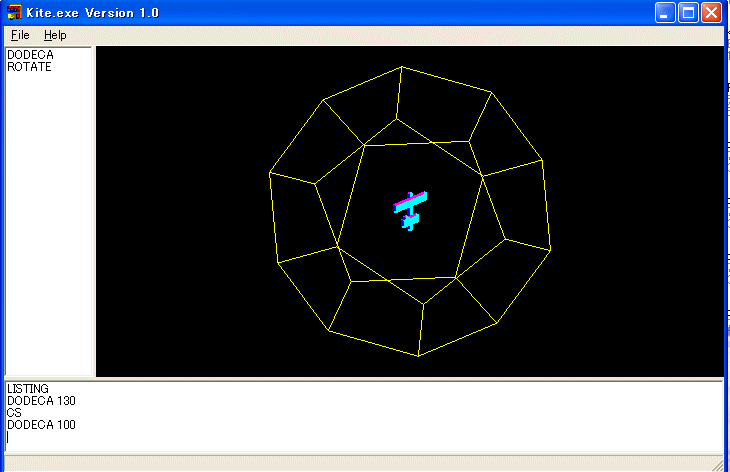
例:これらの立体は次の手続きを実行して、観察しましょう。図を描いた後で、実行すると図が回転します。アニメーションが作れます。
TO ROTATE
FOR :i=0 TO 360 [LOOKAT 500*COS :I 500*SIN :I 500 0 0 0 0 1 0]
END
図形が回転します。
もっと簡単な方法は画面をマウスでドラッグして下さい。図が回転します。プログラミングが下手で制御が難しいですが。
次に中村研究室の学生さん達が作ったプログラムを紹介します。
■ 正四面体(その一):豊田祐子作
TO tetra :a
st2
pu2 fd2 (sqrt 3) * :a / 3
pd2
up 90 pu fd (sqrt 6) * :a / 3
pd
synchro
rt2 150 fd2 :a
rt2 120 fd2 :a
rt2 120 fd2 :a
nonsynchro
rt2 120 fd2 :a
rt2 120 fd2 :a
rt2 120 fd2 :a
end
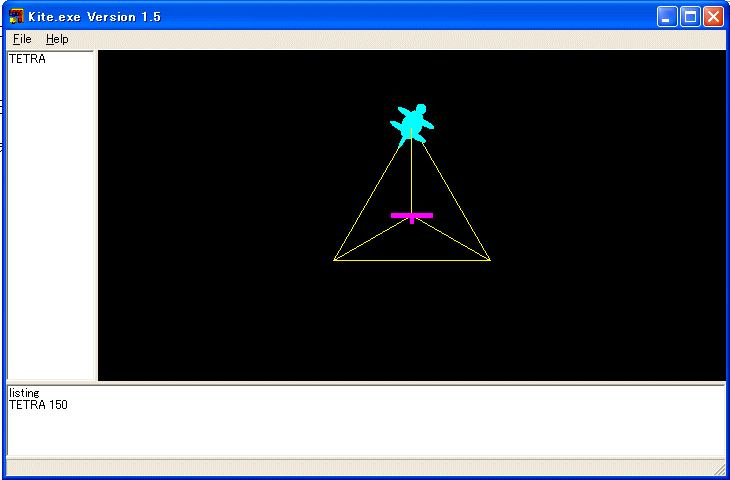
■ 正四面体(その二):豊田祐子作
TO tetra2 :a
fd :a rt 120
fd :a rt 120
fd :a rt 120
pu fd :a / 2
rt 90 fd (sqrt 3) * :a / 6
up 90 fd (sqrt 6) * :a / 3
down 90
down asin (sqrt 6) / 3
pd fd :a
pu bk :a
up asin (sqrt 6) / 3
pd rt 120 down asin (sqrt 6) / 3 fd :a
pu bk :a up asin (sqrt 6) / 3
pd rt 120 down asin (sqrt 6) / 3 fd :a
end
■ 正四面体(その三):豊田祐子作
TO tetras :a
st2
pu2 fd2 (sqrt 3) * :a / 3
pd2
up 90 pu fd (sqrt 6) * :a / 3
pd
synchro surface
setcolor rand rand rand rt2 150 fd2 :a
setcolor rand rand rand rt2 120 fd2 :a
setcolor rand rand rand rt2 120 fd2 :a
nonsynchro surface
polymode
setcolor rand rand rand
rt2 120 fd2 :a
rt2 120 fd2 :a
rt2 120 fd2 :a
nonpolymode
end
■ 立方体:松永弘子作
TO cube :size
polymode setcolor 0 1 0
repeat 4 [fd :size rt 90]
nonpolymode
down 90
polymode setcolor 1 0 0
repeat 4 [fd :size rt 90]
nonpolymode
lt 90 up 90
polymode setcolor 0 0 1
repeat 4 [fd :size rt 90]
nonpolymode
pu fd :size pd up 90
polymode setcolor 1 1 0
repeat 4 [fd :size rt 90]
nonpolymode
pu fd :size down 90 rt 90 pd
polymode setcolor 1 0 1
repeat 4 [fd :size rt 90]
nonpolymode
pu fd :size up 270 pd
polymode setcolor 0 1 1
repeat 4 [fd :size rt 90]
nonpolymode
end
■ 正八面体:松永弘子作
TO hatimentai :size
st2 up 90 pu fd :size/(sqrt 2) down 90
pu2 fd2 :size/(sqrt 2) rt2 135 pd2
nonsynchro repeat 4 [fd2 :size rt2 90]
pd synchro surface
setcolor 1 0 0 fd2 :size rt2 90
setcolor 0 1 0 fd2 :size rt2 90
setcolor 0 0 1 fd2 :size rt2 90
setcolor 1 1 0 fd2 :size rt2 90
nonsynchro nonsurface
down 90 pu fd :size*(sqrt 2)
down 90 synchro surface pd
setcolor 1 0 1 fd2 :size rt2 90
setcolor 0 1 1 fd2 :size rt2 90
setcolor 1 1 1 fd2 :size rt2 90
setcolor 0 1/2 1/2 fd2 :size rt2 90
nonsynchro nonsurface
end
■ 正十二面体(その一):豊田祐子作
TO dodecahedron :a
:B=(:a * cos 36) / (2 * (sin 36 ) * sqrt(3-4 * (cos 36 )* (cos 36 )))
:C=asin (2 / sqrt 5)
push
pu up 90 fd :B
down 90
repeat 5[push fd (:a * cos 36) / (2 * sin 36 ) down :C rt 90
pd repeat 5[fd :a /2 lt 72 fd :a / 2] pu pop lt 72]
pu pop
down 90 fd :B
up 90
rt 36 repeat 5[push fd (:a * cos 36) / (2 * sin 36 ) up :C rt 90
pd repeat 5[fd :a/2 lt 72 fd :a /2] pu pop lt 72]
end
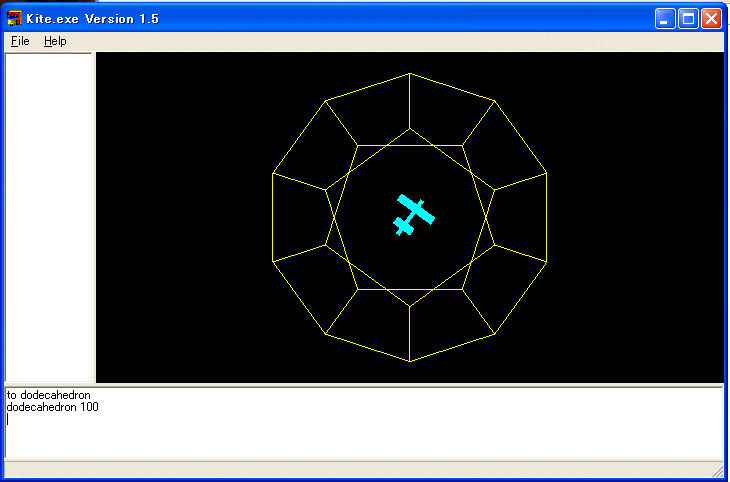
■ 正十二面体(その二):豊田祐子作
TO dodecahedrons :a
:B=(:a * cos 36) / (2 * (sin 36 ) * sqrt(3-4 * (cos 36 )* (cos 36 )))
:C=asin (2 / sqrt 5)
push
pu up 90 fd :B
down 90 push
fd ( :a * cos 36 ) / (2 * sin 36) rt 90
pd polymode setcolor rand rand rand
repeat 5[fd :a / 2 rt 72 fd :a /2 ]
nonpolymode pu pop
repeat 5[polymode setcolor rand rand rand
push fd (:a * cos 36) / (2 * sin 36 ) down :C rt 90
pd repeat 5[fd :a /2 lt 72 fd :a / 2] pu pop lt 72
nonpolymode]
pu pop
down 90 fd :B
up 90 push
lt 36 fd ( :a * cos 36 ) / (2 * sin 36) rt 90
pd polymode setcolor rand rand rand
repeat 5[fd :a / 2 rt 72 fd :a /2 ]
nonpolymode pu pop
rt 36 repeat 5[polymode setcolor rand rand rand
push fd (:a * cos 36) / (2 * sin 36 ) up :C rt 90
pd repeat 5[fd :a/2 lt 72 fd :a /2] pu pop lt 72 nonpolymode]
end
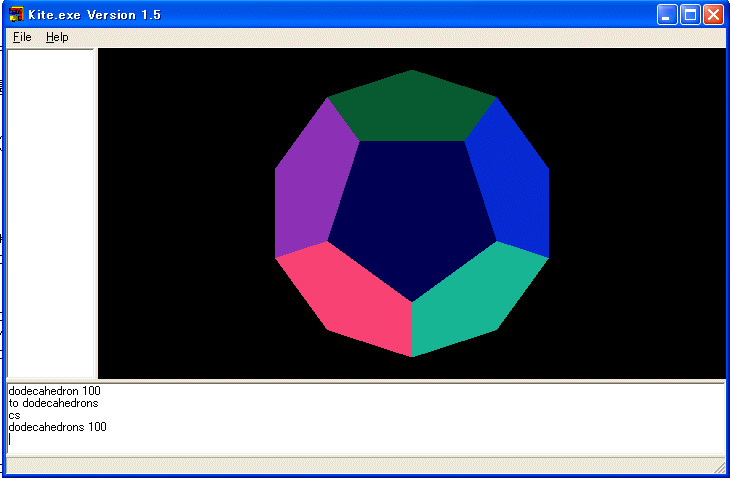
■ 正二十面体(その一):松永弘子作
TO icosa :size
push
pu up 90 fd :size*sin(acos 1/(2*sin 36)) down 90 pd
st2 push2 pu2 fd2 :size/(2* sin 36) pd2 rt2 126
synchro
repeat 5 [fd2 :size rt2 72]
nonsynchro
repeat 5 [fd2 :size rt2 72]
rt2 108
pu pop push down 90 fd :size*(sqrt 6)/3 up 90 rt 36
fd :size/(2*sin 36) lt 126 pd
repeat 5 [
synchro fd :size fd2 0 nonsynchro
lt 72
synchro fd 0 fd2 :size nonsynchro
lt2 72
]
pu pop pu2 pop2
down 90 fd :size*(sqrt 6)/3 down2 90 fd2 :size*(sqrt 6)/3 down2 90
fd :size*sin(acos 1/(2*sin 36)) down 90 pd
fd2 :size/(2*sin 36) pd2 rt2 126
synchro
repeat 5 [fd2 :size rt2 72]
nonsynchro
repeat 5 [fd2 :size rt2 72]
end
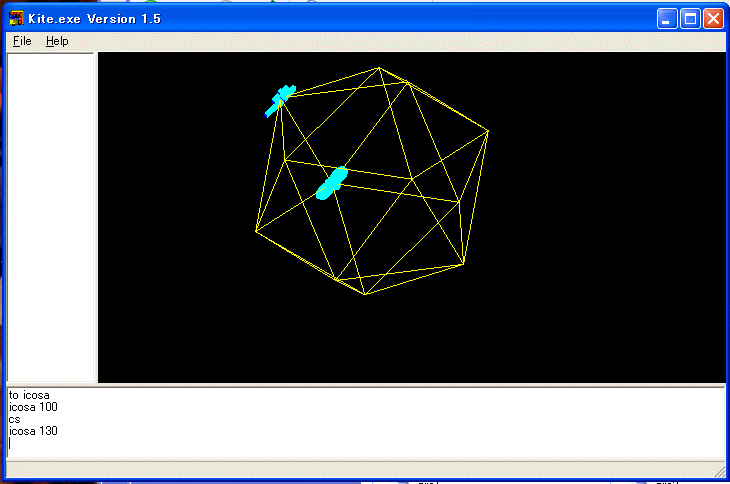
■ 正二十面体(その二):松永弘子作
TO icosa :size
push
pu up 90 fd :size*sin(acos 1/(2*sin 36)) down 90 pd
st2 push2 pu2 fd2 :size/(2* sin 36) pd2 rt2 126
synchro
repeat 5 [fd2 :size rt2 72]
nonsynchro
synchro surface
repeat 5 [setcolor rand rand rand fd2 :size rt2 72]
nonsynchro nonsurface
rt2 108
pu pop push down 90 fd :size*(sqrt 6)/3 up 90 rt 36
fd :size/(2*sin 36) lt 126 pd
repeat 5 [
synchro surface
setcolor rand rand rand
fd :size fd2 0
nonsynchro nonsurface
lt 72
synchro surface
setcolor rand rand rand fd 0
fd2 :size
nonsynchro nonsurface
lt2 72
]
pu pop pu2 pop2
down 90 fd :size*(sqrt 6)/3 down2 90 fd2 :size*(sqrt 6)/3 down2 90
fd :size*sin(acos 1/(2*sin 36)) down 90 pd
fd2 :size/(2*sin 36) pd2 rt2 126
synchro surface
repeat 5 [setcolor rand rand rand fd2 :size rt2 72]
nonsynchro nonsurface
synchro surface
repeat 5 [setcolor rand rand rand fd2 :size rt2 72]
nonsynchro nonsurface
end
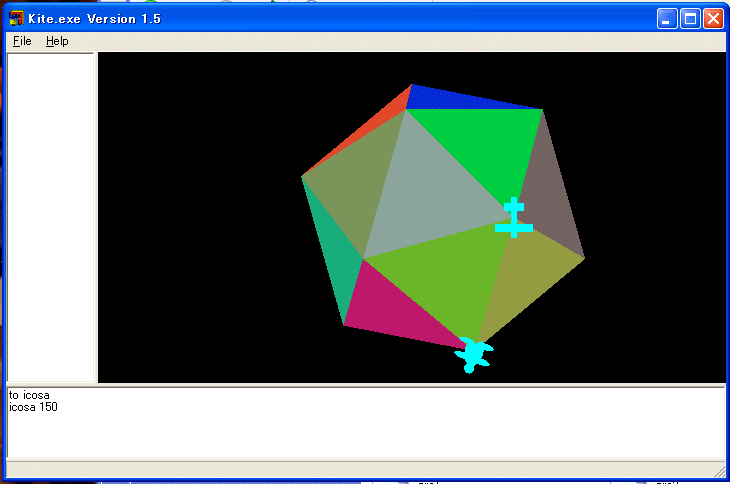
■ 星形小十二面体:豊田祐子作
TO pentagon :a :b :c :d :e :s
pu
get 1 :e
polymode
pu2 get 2 :a
pd2 get 2 :c
toward2
fd2 :s
get 2 :a
nonpolymode
get 1 :a
polymode
pu2 get 2 :b
pd2 get 2 :d
toward2
fd2 :s
get 2 :b
nonpolymode
get 1 :c
polymode
pu2 get 2 :b
pd2 get 2 :e
toward2
fd2 :s
get 2 :b
nonpolymode
end
TO smallstellateddodecahedron :a
push
st2
push2
pu up 90 fd :a * sin acos 1 /( 2 * sin 36 ) put 1 0
pu2 fd2 :a / (2 * sin 36) rt2 126 put 2 1
fd2 :a rt2 72 put 2 2
fd2 :a rt2 72 put 2 3
fd2 :a rt2 72 put 2 4
fd2 :a rt2 72 put 2 5
fd2 :a rt2 72
pop pop2
push push2
down 90 fd (:a * sqrt 6 )/3
fd :a * sin acos 1 /( 2 * sin 36 ) put 1 6
down2 90 fd2 (:a * sqrt 6 )/3 up2 90
lt2 180 fd2 :a / (2 * sin 36) rt2 126 put 2 7
fd2 :a rt2 72 put 2 8
fd2 :a rt2 72 put 2 9
fd2 :a rt2 72 put 2 10
fd2 :a rt2 72 put 2 11
fd2 :a rt2 72
pop pop2
pd pd2
setcolor rand rand rand
pentagon 0 3 7 8 5 :a
setcolor rand rand rand
pentagon 0 2 11 7 4 :a
setcolor rand rand rand
pentagon 0 1 10 11 3 :a
setcolor rand rand rand
pentagon 0 5 9 10 2 :a
setcolor rand rand rand
pentagon 0 4 8 9 1 :a
setcolor rand rand rand
pentagon 1 2 3 4 5 :a
setcolor rand rand rand
pentagon 1 9 6 11 2 :a
setcolor rand rand rand
pentagon 1 5 8 6 10 :a
setcolor rand rand rand
pentagon 2 10 6 7 3 :a
setcolor rand rand rand
pentagon 3 11 6 8 4 :a
setcolor rand rand rand
pentagon 4 7 6 9 5 :a
setcolor rand rand rand
pentagon 7 11 10 9 8 :a
end
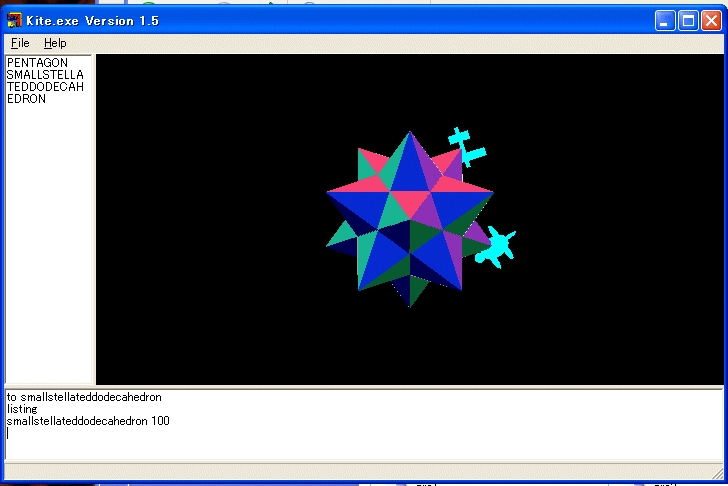
■ 星形大十二面体:松永弘子作
TO pentagon :a :b :c :d :e
polymode setcolor rand rand rand pu pu2
get 1 :e pd pd2 get 2 :a push2 get 2 :c
toward2 fd2 (1-(1/(4*(cos 36)*(cos 36))))*distance2
pop2 nonpolymode polymode setcolor rand rand rand pu pu2
get 1 :d pd pd2 get 2 :e push2 get 2 :b
toward2 fd2 (1-(1/(4*(cos 36)*(cos 36))))*distance2
pop2 nonpolymode polymode setcolor rand rand rand pu pu2
get 1 :c pd pd2 get 2 :d push2 get 2 :a
toward2 fd2 (1-(1/(4*(cos 36)*(cos 36))))*distance2
pop2 nonpolymode
end
TO hosigatadai12mentai :size
pu rt 126 put 1 1 fd :size rt 72 put 1 2
fd :size rt 72 put 1 3 fd :size rt 72 put 1 4
fd :size rt 72 put 1 0 fd :size rt 72
fd :size/2 lt 90 push up asin 2/sqrt 5
fd :size*(1+cos 36)/(2*sin 36) rt 126
put 1 5 fd :size rt 72 put 1 6 pop rt 90 fd :size/2 rt 72
fd :size/2 lt 90 push up asin 2/sqrt 5
fd :size*(1+cos 36)/(2*sin 36) rt 126
put 1 7 fd :size rt 72 put 1 8 pop rt 90 fd :size/2 rt 72
fd :size/2 lt 90 push up asin 2/sqrt 5
fd :size*(1+cos 36)/(2*sin 36) rt 126
put 1 9 fd :size rt 72 put 1 10 pop rt 90 fd :size/2 rt 72
fd :size/2 lt 90 push up asin 2/sqrt 5
fd :size*(1+cos 36)/(2*sin 36) rt 126
put 1 11 fd :size rt 72 put 1 12 pop rt 90 fd :size/2 rt 72
fd :size/2 lt 90 push up asin 2/sqrt 5
fd :size*(1+cos 36)/(2*sin 36) rt 126
put 1 13 fd :size rt 72 put 1 14 pop rt 90 fd :size/2 rt 72
rt 54 fd :size/(2*sin 36)
up 90 fd :size*(cos 36)*(cos 60)/((sin 36)*sqrt (1-(cos 36)*(cos 36)-(cos 60)*(cos 60)))
down 90 rt 36 up 180 fd :size/(2*sin 36) rt 126
put 1 15 fd :size rt 72 put 1 16
fd :size rt 72 put 1 17 fd :size rt 72 put 1 18 fd :size rt 72 put 1 19
pentagon 0 3 7 15 13
pentagon 0 11 18 7 2
pentagon 0 14 15 18 10
pentagon 1 4 9 19 5
pentagon 1 13 17 9 3
pentagon 1 6 19 17 12
pentagon 2 8 18 16 14
pentagon 2 5 16 11 4
pentagon 3 10 17 15 6
pentagon 4 12 16 19 8
pentagon 14 12 10 8 6
pentagon 13 5 7 9 11
st2 pu2 get 2 19 get 1 0 toward2 fd2 (1/2)*distance2 put 2 20 get 1 20
end
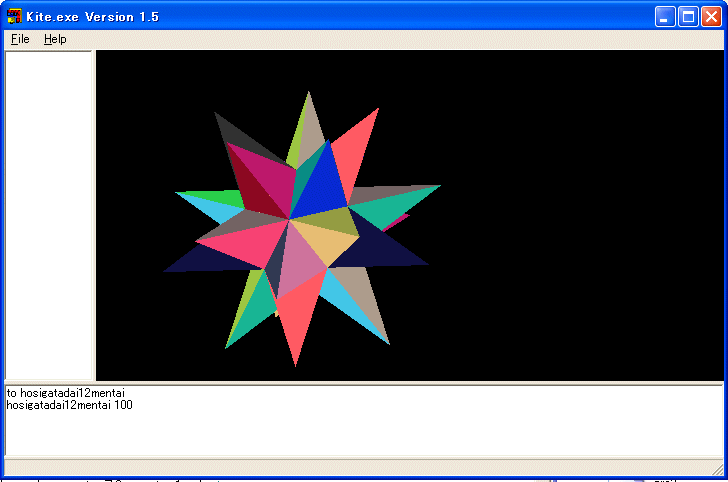
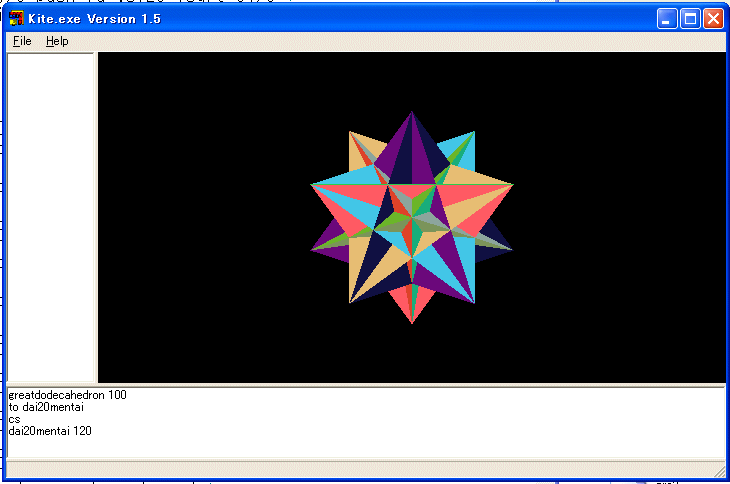
■ 大十二面体:豊田祐子作
TO greatdodecahedron :a
push
st2
push2
pu up 90 fd :a * sin acos 1 /( 2 * sin 36 ) put 1 0
pu2 fd2 :a / (2 * sin 36) rt2 126 put 2 1
fd2 :a rt2 72 put 2 2
fd2 :a rt2 72 put 2 3
fd2 :a rt2 72 put 2 4
fd2 :a rt2 72 put 2 5
fd2 :a rt2 72
pop pop2
push push2
down 90 fd (:a * sqrt 6 )/3
fd :a * sin acos 1 /( 2 * sin 36 ) put 1 6
down2 90 fd2 (:a * sqrt 6 )/3 up2 90
lt2 180 fd2 :a / (2 * sin 36) rt2 126 put 2 7
fd2 :a rt2 72 put 2 8
fd2 :a rt2 72 put 2 9
fd2 :a rt2 72 put 2 10
fd2 :a rt2 72 put 2 11
fd2 :a rt2 72
pop pop2
polymode setcolor rand rand rand
get 1 1 pd get 1 2 get 1 3 get 1 4 get 1 5 get 1 1
nonpolymode pu
polymode setcolor rand rand rand
get 1 0 pd get 1 5 get 1 9 get 1 10 get 1 2 get 1 0
nonpolymode pu
polymode setcolor rand rand rand
get 1 11 pd get 1 7 get 1 4 get 1 0 get 1 2 get 1 11
nonpolymode pu
polymode setcolor rand rand rand
get 1 4 pd get 1 0 get 1 2 get 1 11 get 1 7 get 1 4
nonpolymode pu
polymode setcolor rand rand rand
get 1 5 pd get 1 0 get 1 3 get 1 7 get 1 8 get 1 5
nonpolymode pu
polymode setcolor rand rand rand
get 1 4 pd get 1 8 get 1 9 get 1 1 get 1 0 get 1 4
nonpolymode pu
polymode setcolor rand rand rand
get 1 7 pd get 1 8 get 1 9 get 1 10 get 1 1 get 1 7
nonpolymode pu
polymode setcolor rand rand rand
get 1 8 pd get 1 4 get 1 3 get 1 11 get 1 6 get 1 8
nonpolymode pu
polymode setcolor rand rand rand
get 1 9 pd get 1 5 get 1 4 get 1 7 get 1 6 get 1 9
nonpolymode pu
polymode setcolor rand rand rand
get 1 10 pd get 1 1 get 1 5 get 1 8 get 1 6 get 1 10
nonpolymode pu
polymode setcolor rand rand rand
get 1 11 pd get 1 2 get 1 1 get 1 9 get 1 6 get 1 11
nonpolymode pu
polymode setcolor rand rand rand
get 1 6 pd get 1 7 get 1 3 get 1 2 get 1 10 get 1 6
nonpolymode pu
end
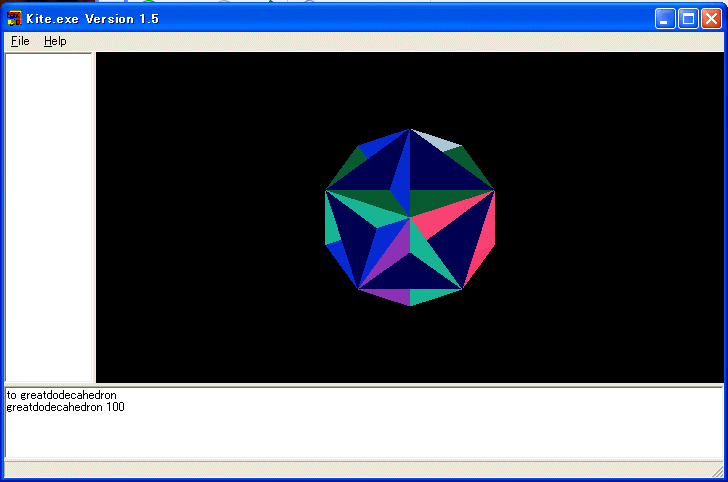
■ 大二十面体:松永弘子作
TO dai20mentai :size
push pu up 90 fd :size*sin(acos 1/(2*sin 36)) down 90 put 1 0 pop
st2 push2 pu2 fd2 :size/(2* sin 36) put 2 1
lt2 126 fd2 :size lt2 72 put 2 2
fd2 :size lt2 72 put 2 3 fd2 :size lt2 72 put 2 4
fd2 :size lt2 72 put 2 5 pop2
down 90 fd :size*(sqrt 6)/6 push fd :size*(sqrt 6)/6
fd :size*sin(acos 1/(2*sin 36))
down 90 put 1 6
down2 90 fd2 :size*(sqrt 6)/6 push2
fd2 :size*(sqrt 6)/6 up2 90 lt2 36 fd2 :size/(2*sin 36)
lt2 126 put 2 7
fd2 :size lt2 72 put 2 8 fd2 :size lt2 72 put 2 9
fd2 :size lt2 72 put 2 10 fd2 :size lt2 72 put 2 11
get 2 0 pd2 polymode setcolor rand rand rand
get 2 9 get 2 11 get 2 0 nonpolymode pu2
get 2 0 pd2 polymode setcolor rand rand rand
get 2 8 get 2 10 get 2 0 nonpolymode pu2
get 2 0 pd2 polymode setcolor rand rand rand
get 2 7 get 2 9 get 2 0 nonpolymode pu2
get 2 0 pd2 polymode setcolor rand rand rand
get 2 11 get 2 8 get 2 0 nonpolymode pu2
get 2 0 pd2 polymode setcolor rand rand rand
get 2 10 get 2 7 get 2 0 nonpolymode pu2
get 2 6 pd2 polymode setcolor rand rand rand
get 2 4 get 2 2 get 2 6 nonpolymode pu2
get 2 6 pd2 polymode setcolor rand rand rand
get 2 5 get 2 3 get 2 6 nonpolymode pu2
get 2 6 pd2 polymode setcolor rand rand rand
get 2 1 get 2 4 get 2 6 nonpolymode pu2
get 2 6 pd2 polymode setcolor rand rand rand
get 2 2 get 2 5 get 2 6 nonpolymode pu2
get 2 6 pd2 polymode setcolor rand rand rand
get 2 3 get 2 1 get 2 6 nonpolymode pu2
get 2 1 pd2 polymode setcolor rand rand rand
get 2 8 get 2 4 get 2 1 nonpolymode pu2
get 2 1 pd2 polymode setcolor rand rand rand
get 2 10 get 2 8 get 2 1 nonpolymode pu2
get 2 1 pd2 polymode setcolor rand rand rand
get 2 3 get 2 10 get 2 1 nonpolymode pu2
get 2 2 pd2 polymode setcolor rand rand rand
get 2 9 get 2 5 get 2 2 nonpolymode pu2
get 2 2 pd2 polymode setcolor rand rand rand
get 2 11 get 2 9 get 2 2 nonpolymode pu2
get 2 2 pd2 polymode setcolor rand rand rand
get 2 4 get 2 11 get 2 2 nonpolymode pu2
get 2 3 pd2 polymode setcolor rand rand rand
get 2 5 get 2 7 get 2 3 nonpolymode pu2
get 2 3 pd2 polymode setcolor rand rand rand
get 2 7 get 2 10 get 2 3 nonpolymode pu2
get 2 4 pd2 polymode setcolor rand rand rand
get 2 8 get 2 11 get 2 4 nonpolymode pu2
get 2 5 pd2 polymode setcolor rand rand rand
get 2 9 get 2 7 get 2 5 nonpolymode pu2
pop pop2
end