最終更新日 2004年1月28日
空間LOGO : KITEの使い方
では、KITE.EXE を立ち上げてみましょう。
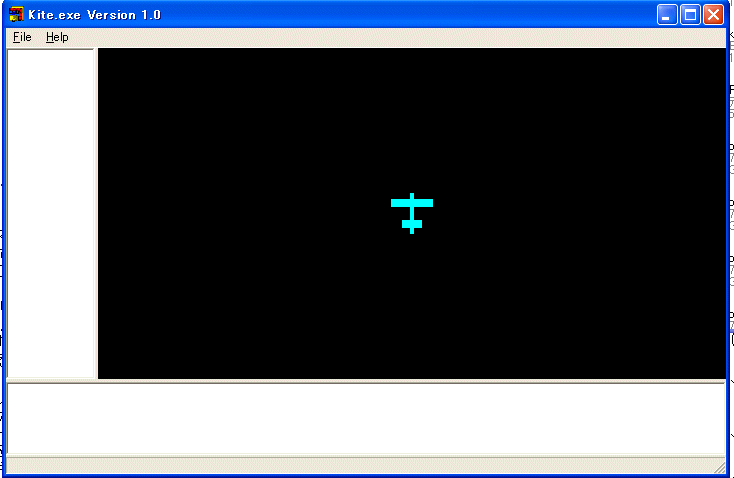
画面が三つの領域に分かれています。黒い画面がタートルが線画を描くキャンバスです。画面の真中にいる飛行機が一匹目のタートルです。下の領域がタートルに対する命令を打ち込む領域です。左側の領域がPRINT命令の結果やLISTING命令の結果が表示される領域です。それぞれの大きさを変化させることも出来ます。
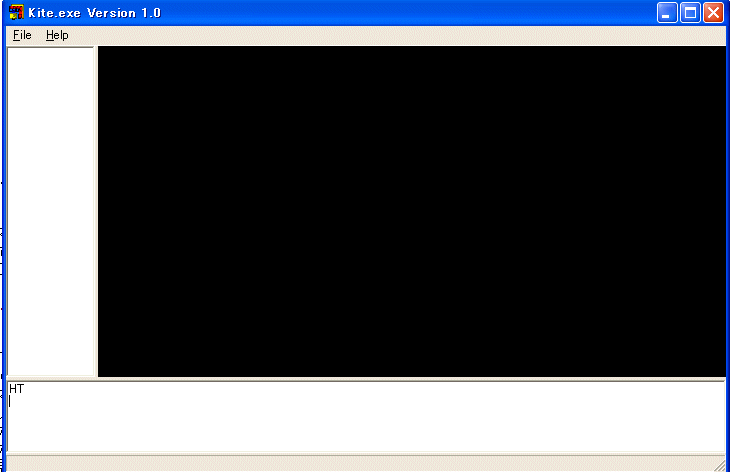
下の領域にHTと打ち込みEnterキーを押すと飛行機が消えます。
HT は HideTurtle の省略形です。以下、Enterキーを押すという指示は省略します。STと打つと飛行機が現れます。ST は ShowTurtle の省略形です。飛行機を消し、ST2と打ち込むと亀が現れます。
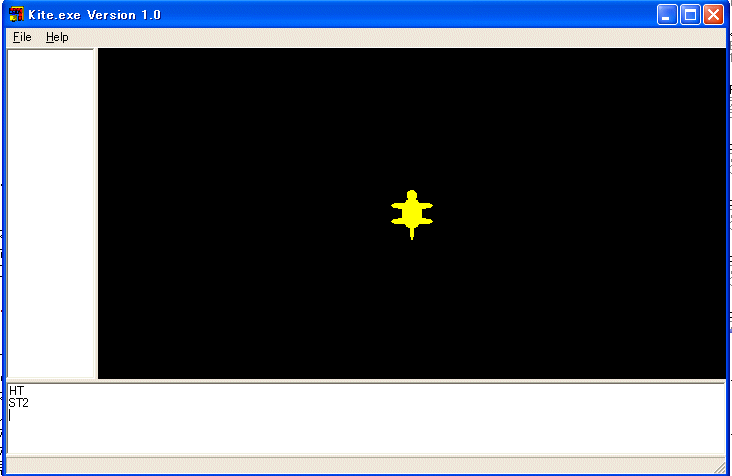
これが二匹目のタートルです。命令はすべて半角文字で指示します。このソフトは大文字と小文字を区別しません。従って、例えば、HT命令はhtでもHtでもhTでもいいです。CSと打ち込むと初期状態に戻ります。CS は ClearScreen の省略形です。タートル(亀)は二匹います。初期状態では二匹のタートルは三次元空間の原点(0,0,0)に居て、一番目のタートルだけが見えています。XY 平面が画面で、原点は画面の中央です。Z 軸は画面に垂直で手前が正の方向です。両方のタートルがペンを下ろしています。移動すると線を描きます。ペンを上げると移動しても線を描きません。二匹目のタートルに対する命令や関数は 2 の添字が付きます。PU命令は一番目のタートルがペンを上げます。PU は PenUp の省略形です。PU2命令は二番目のタートルがペンを上げます。PD命令は一番目のタートルがペンを下ろします。PD は PenDown の省略形です。PD2命令は二番目のタートルがペンを下ろします。TOWARD 命令と DISTANCE 関数が二つのタートルで仕様が異なりますが、他の命令や関数は2が付けば二番目のタートルに対する同様な命令や関数です。
CS命令を実行して、初期状態に戻してください。タートルは原点でXY平面に平行でY軸の正の向きを向いて背中をZ軸の正の方向に向けています。色々確かめていると分かってくると思いますので最初はあまり気にしないで下さい。FD 100 を実行します。(即ち、下の領域に FD 100 と打ち込みEnterキーを押す。FD と 100 の間にはスペースが必要です。以下、同様)。
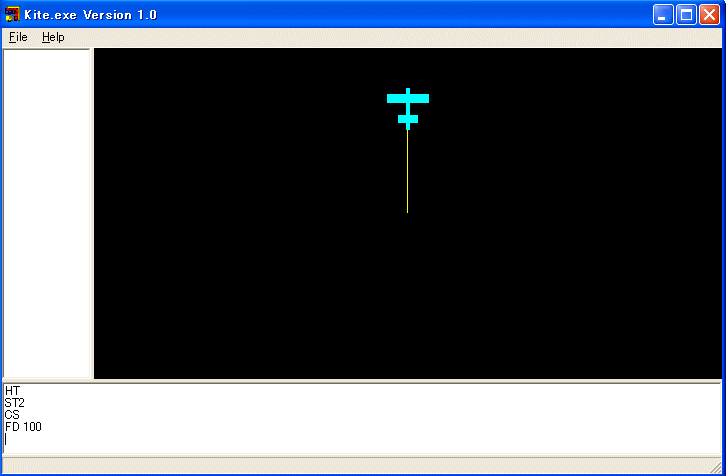
飛行機が100単位だけ前進します。FD は FORWARD の省略形です。RT 90 を実行します。
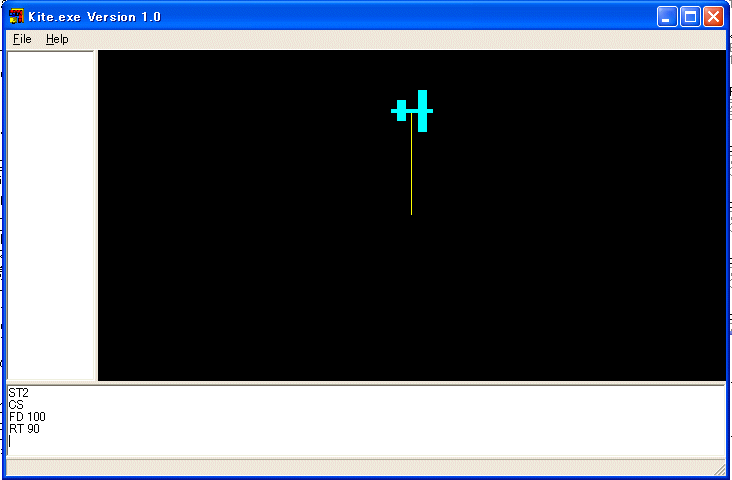
飛行機が右に90度回転します。RT は RIGHT の省略形です。FD 100 RT 90 を四回繰り返すと正方形を描いて元の位置に戻ります。
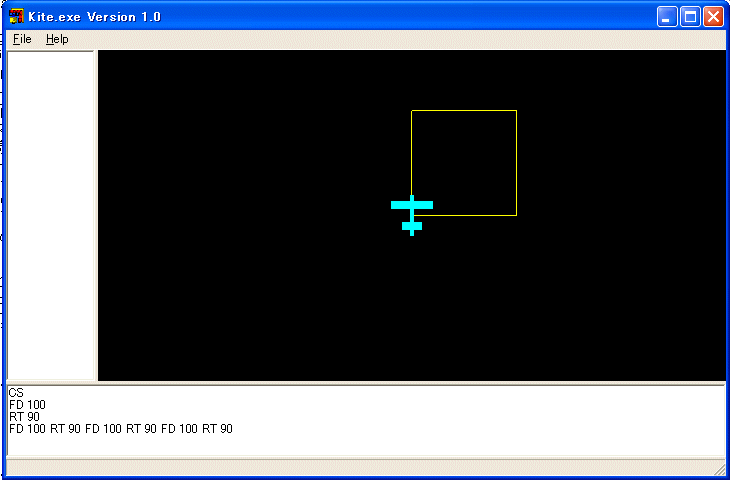
FD 数値は数値の値だけ前進せよという命令で、BK 数値は数値の値だけ後退せよという命令で、BK は BACK の省略形です。RT 数値は右回りに数値の値だけ回転せよという命令で、LT 数値は左回りに数値の値だけ回転せよという命令で、LT は LEFT の省略形です。
同じことを何回も繰り返すのは大変です。REPEAT 命令を使うと楽が出来ます。
REPEAT 4 [FD 100 RT 90]
とすれば、[ と ] の間の命令を 4 回繰り返します。従って、この命令だけで正方形を描きます。
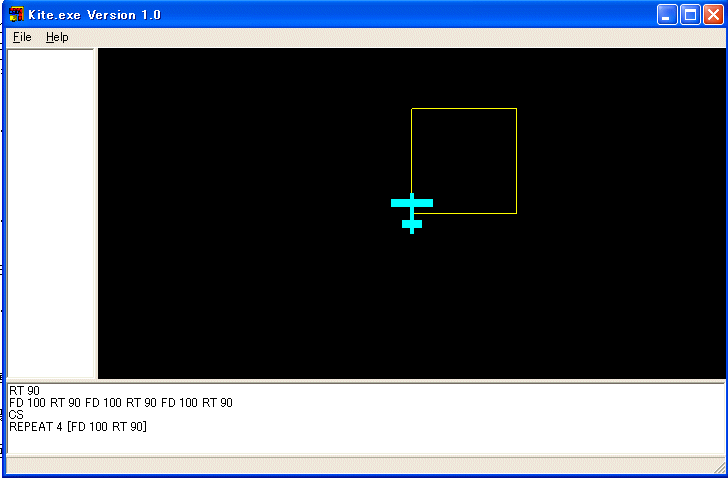
REPEAT 数値 [ 命令の列 ] で命令の列を数値の値の回数繰り返します。正三角形、正五角形、正六角形、正七角形、星型正五角形、星型正七角形など色々描いて見ましょう。
正方形を何個も描きたい時、何時も REPEAT 4 [FD 100 RT 90] と打ち込むのは大変です。コンピュータに正方形の描き方を教えてやりましょう。TO SHIKAKU と打ち込みます。
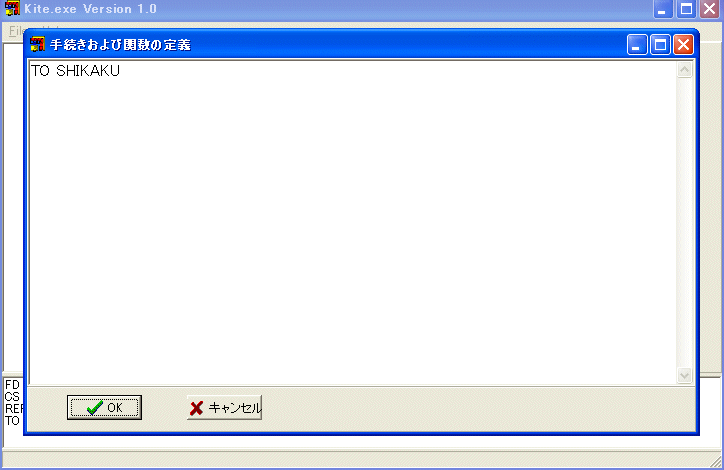
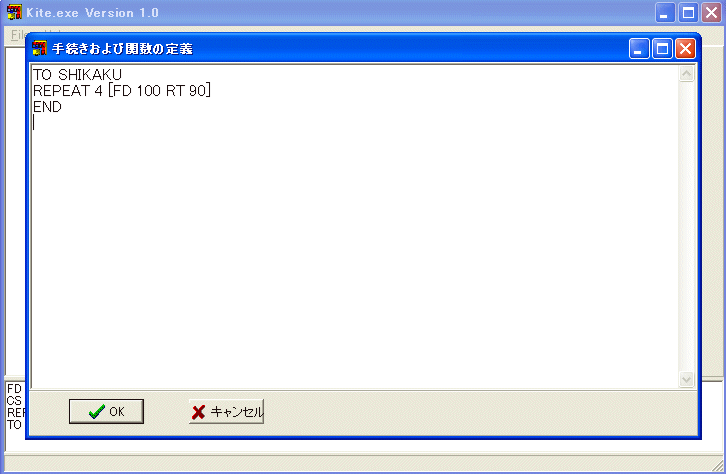
手続きや関数を定義する為のダイアログボックスが開きます。 ダイアログボックスのメモの一行目に TO SHIKAKU と書いてあります。二行目に REPEAT 4 [FD 100 RT 90] と打ち込み、三行目に END と打ち込みます。ダイアログボックスのメモが
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
となっていることを確かめたら、OK ボタンを押します。
定義の最後には必ず END と打ち込んでください。END が手続きや関数の定義の終了の印で、必ず必要です。
■■■■■■■■■■
● 手続きの定義の仕方 ●
SHIKAKU という名前の手続きを定義するには、コマンドラインに(即ち、下側の領域に) TO SHIKAKU と打ち込みます。手続きや関数を定義する為のダイアログボックスが開きます。 ダイアログボックスのメモの一行目に TO SHIKAKU と書いてあります。二行目に REPEAT 4 [FD 100 RT 90] と打ち込み、三行目に END と打ち込みます。ダイアログボックスのメモは
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
となります。ダイアログボックスの下のほうにある OK と描かれたボタンを押します。これで SHIKAKU という手続きをコンピュータが理解するようになります。
コマンドラインに(即ち、下側の領域に)
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
と打ち込むのではありませんので、くれぐれも間違わないようにしてください。
■■■■■■■■■■
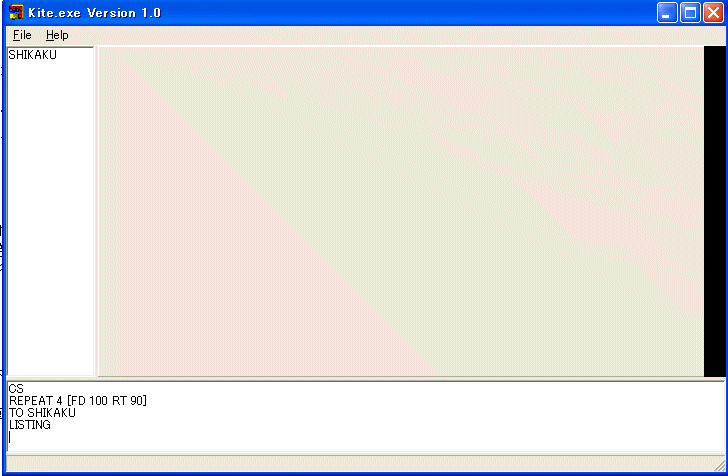
LISTING 命令を実行してみます。左の領域に SHIKAKU と表示されるはずです。
SHIKAKU という命令をコンピュータが覚えました。CS 命令を実行し、初期画面に戻し、SHIKAKU と打ち込んでEnterキーを押して下さい。
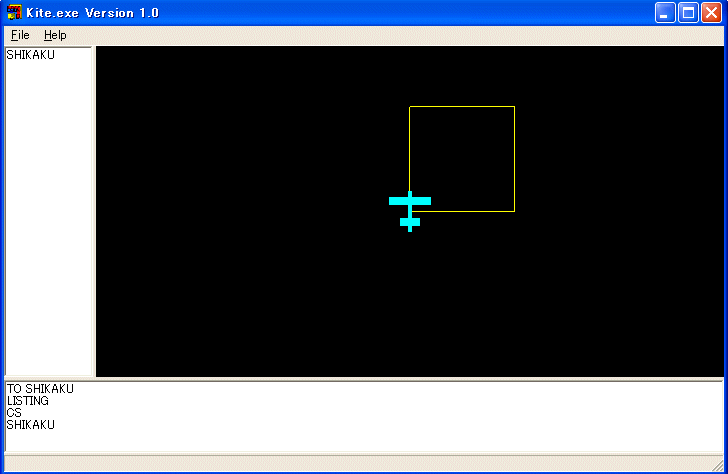
正方形が描かれたはずです。エラーが表示されたら、何と言っているか良く読んでください。例えば SHIKAKU と打ち込んだつもりが SIKAKU の場合はもう一度打ち直せば良いです。
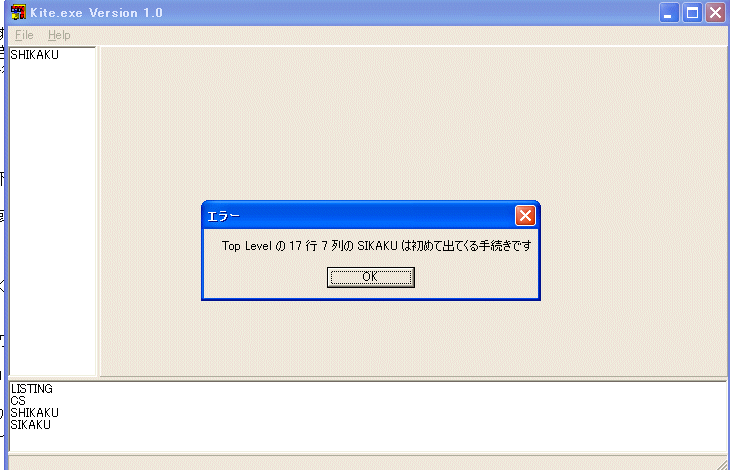
例えば、
TO SHIKAKU
REPAET 4 [FD 100 RT 90]
END
と定義して、SHIKAKU を実行すると次のようなエラー表示があります。
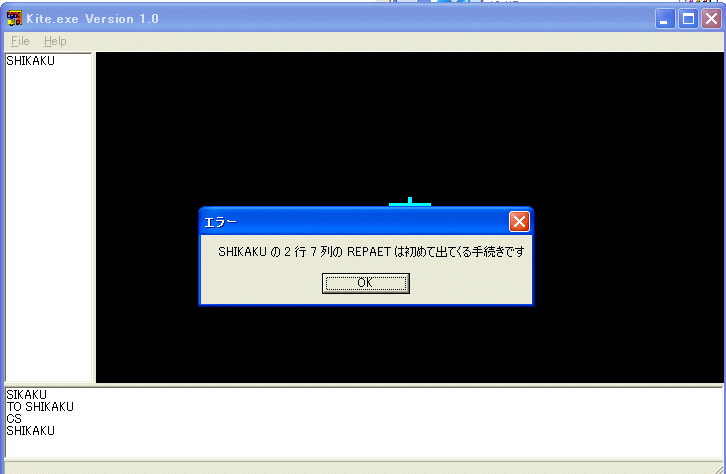
SHIKAKU の定義の中にエラーがあると言っているので、もう一度 TO SHIKAKU を実行しますコンピュータに教えた SHIKAKU の定義の書かれたダイアログボックスが出てきますから、間違いを直して、OK ボタンを押して、やり直してください。この自分で定義した命令も FD や RT のような組み込みの手続きと同様に使うことが出来ます。
REPEAT 6 [SHIKAKU RT 60]
と実行して下さい。
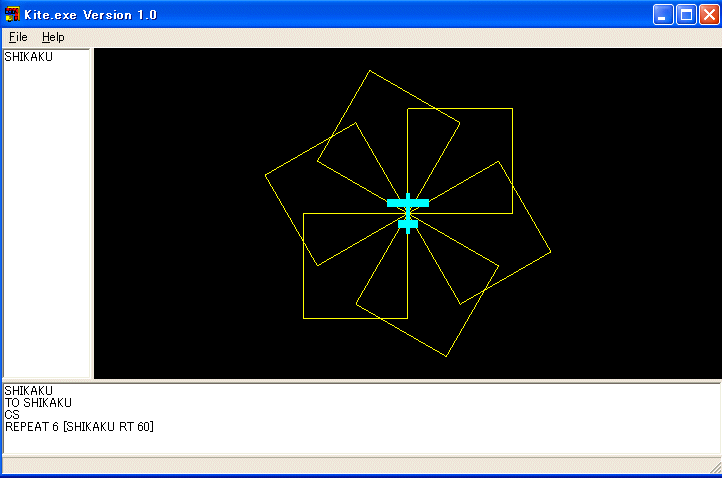
原点を中心に正方形を60度づつ回転しながら6個描いたはずです。
■■■■■■■■■■
● 画面を拡大・縮小したり、ダイアログボックスを表示して絵が消えた場合 ●
本来なら絵が消えないようにプログラミングすべきですが、今のところ方法が分かりません。REPAINT 命令を打ち込んで下さい。絵が復元できます。
■■■■■■■■■■
毎回同じ大きさの正方形では面白くありません。TO SHIKAKU と打ち込んでください。
KITE を新たに立ち上げたのでなければ、
TO SHIKAKU
REPEAT 4 [FD 100 RT 90]
END
と書かれたダイアログボックスが現れるはずです。次のように修正します。
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
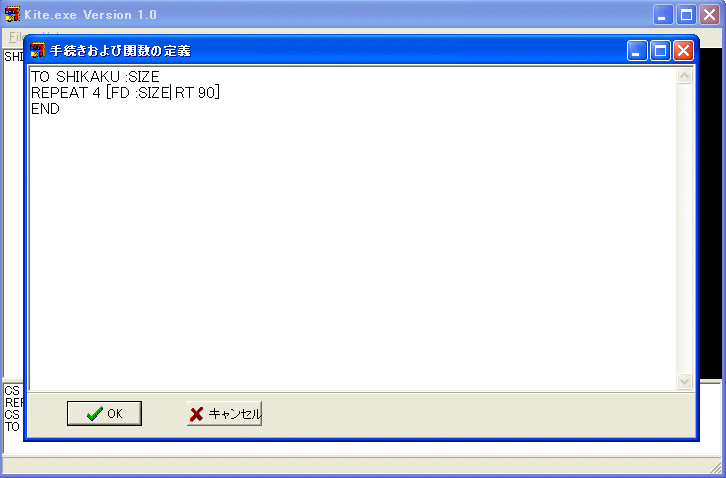
正しく打ち込めたことを確かめて、OK ボタンを押します。
■■■■■■■■■■
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
というプログラムを示すと一行目から全部改めて打ち込んで
TO SHIKAKU
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
となっている人がよくいます。これはエラーになります。初めて TO SHIKAKU を実行したときもコンピュータが作ってくれる TO SHIKAKU を利用して、ダイアログボックスのメモの内容を
TO SHIKAKU :SIZE
REPEAT 4 [FD :SIZE RT 90]
END
としてください。
■■■■■■■■■■
CS 命令で、画面を初期化し、SHIKAKU 50 と打ち込みます。
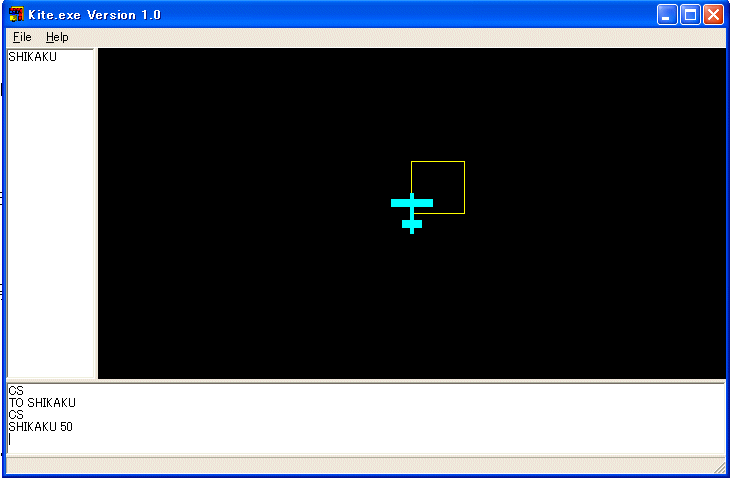
50 単位の正方形を描くはずです。次に、
FOR :I = 10 TO 150 STEP 20 [SHIKAKU :I ]
を実行します。
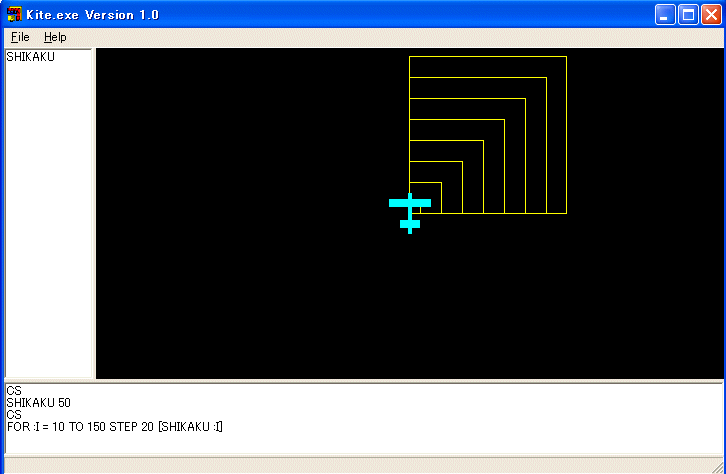
この命令は :I を最初は 10 とし、その値が 150 を超えなければ、一回 [ と ] で囲まれた命令の列を実行し、:I に 20 を加え、その値が 150 を超えなければ、一回 [ と ] で囲まれた命令の列を実行し、:I に 20 を加え、その値が 150 を超えなければ、一回 [ と ] で囲まれた命令の列を実行しを繰り返します。従って、10, 30, 50, 70, 90, 110, 130, 150 単位の正方形を続けて描きます。
■■■■■■■■■■
● 作ったプログラムを保存したい時 ●
作ったプログラムはメニューの Fileの Save で保存することが出来ます。
その時覚えているすべてのプログラムを保存します。ファイル名は任意の名前を付けれます。エディタで覗いてみると分かりますが単なるテキストファイルです。従って、各自の好みのエディタでプログラムを作り、メニューの File の Open でプログラムを読み込み、コンピュータに自作の命令を実行させることも出来ます。
保存したプログラムはメニューの File の Open でプログラムを読み込むことが出来ます。どのような手続きや関数が読み込まれたかは LISTING 命令で確かめることが出来ます。
■■■■■■■■■■
三角形を描く手続きを定義しましょう。
TO SANKAKU :SIZE
REPEAT 3 [FD :SIZE RT 120]
END
で定義できます。いったん定義した手続きは自由に使うことが出来ます。家を描く手続きを定義しましょう。正方形と正三角形の手続きを続けて
TO HAUSE :SIZE
SHIKAKU :SIZE SANKAKU :SIZE
END
で良いと思ったかも知れません。しかしだめです。HAUSE 100 としてみましょう。
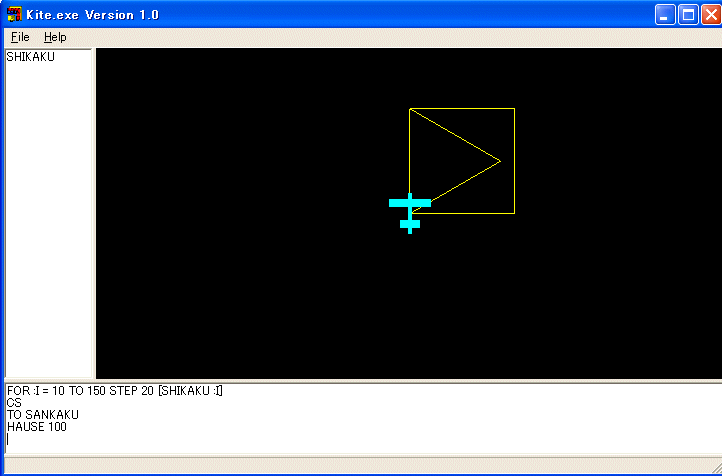
手続きの描き初めと描き終わりのタートルの状態(位置と姿勢)に注意する必要があります。修正して、
TO HAUSE :SIZE
SHIKAKU :SIZE FD :SIZE RT 30 SANKAKU :SIZE
END
とすれば、家を描きます。
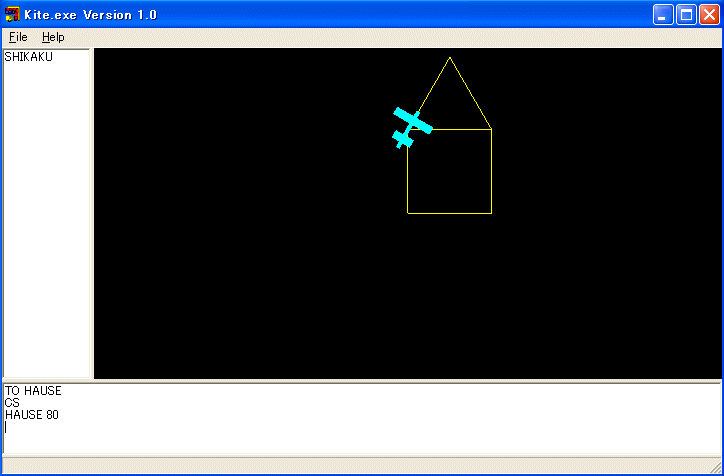
しかし、使い方にも拠りますが、次のように定義するほうが使い易い手続きになります。
TO HAUSE :SIZE
SHIKAKU :SIZE FD :SIZE RT 30 SANKAKU :SIZE LT 30 BK :SIZE
END
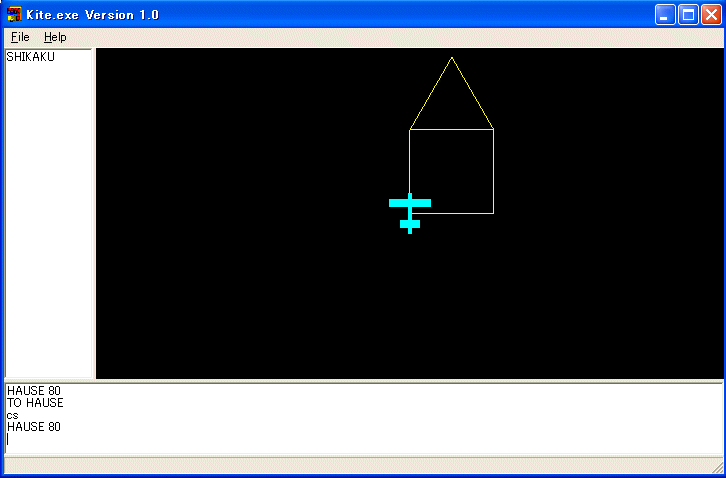
多くの場合、描きはじめと同じ状態にタートルが戻るように手続きを定義しておくと使い易い手続きになる場合が多いようです。勿論、コッホ曲線のような例外もあります。
■■■■■■■■■■
● 作った図形を印刷したい時 ●
KITE で描いた画面を印刷したい時は、メニューの File の Print を実行します。しかし、一般には、初期設定では、画面の背景が黒で、ペンの色が黄色です。そのまま印刷するとインクが無駄になります。印刷したい時は、背景を SetBackColor 数式1 数式2 数式3 命令で白にしておくほうが良いです。SetBackColor 命令の引数は RGB 形式で色を指定します。数式1 の値が赤の明るさ、数式2 の値が緑の明るさ、数式3 の値が青の明るさで、1 1 1 は白、 0 0 0 は黒、 1 0 0 は赤、 0 1 0 は緑、 0 0 1 は青、 1 1 0 は黄色、 0.5 0.5 0.5 は灰色などです。それぞれの数値は 0 から 1 の実数値で指定します。背景色を白にしたときは、SetColor 数式1 数式2 数式3 命令でペンの色を黒などの見やすい色に変えて描いたほうが良いです。初期設定で、背景色を黒にしているのは、OpenGL のデフォルトが黒で、画面で見るには黒のほうが見やすいと考えたからです。印刷するときに自動的に色を反転して印刷するようにすると良いとも考えますが、コンピュータグラフィックスの経験が少なくて、プログラムの仕方が分かりません。今後の課題とさせてください。
■■■■■■■■■■
繰り返しをさせるには、現代的なプログラミング言語では再帰呼び出しという手法がよく使われます。効率が悪いと昔は嫌われましたが、コンピュータの性能が良くなった現代は積極的に使うべきです。慣れれば、見やすいプログラミングが出来ます。TO POLY と打ち込んで下さい。ダイアログボックスのメモに次のように打ち込みます。
TO POLY :SIZE :ANGLE
FD :SIZE RT :ANGLRE
POLY :SIZE :ANGLE
END
と打ち込み、OK ボタンを押して下さい。:SIZE や :ANGLE は命令(普通は手続きといいます) POLY の引数といいます。引数をもつ手続きを定義するときでも TO POLY でいいです。TO POLY :SIZE :ANGLE として呼び出すと後で文句を言います。さて、 POLY 50 60 を実行して下さい。50 単位の正六角形を描き続きます。Esc キーを押して下さい。すぐには停止しないかも分かりませんが、Esc キーを何度か押すと描くのを停止します。
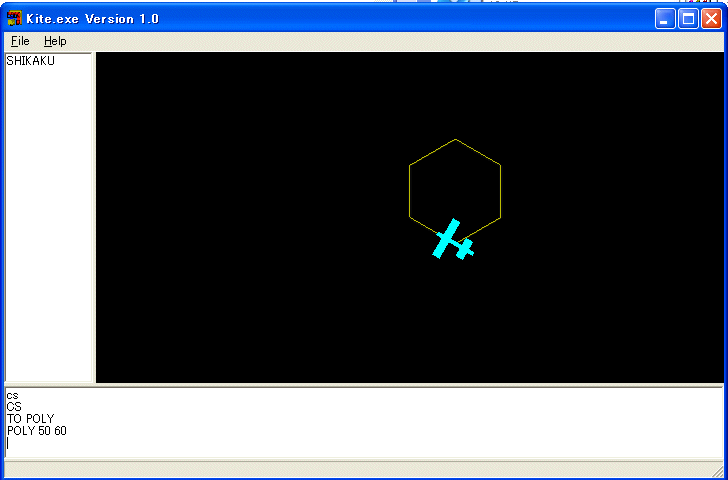
POLY という命令は次のように実行します。POLY 50 60 という命令をされたコンピュータは POLY の定義を調べて、POLY が二つの引数 :SIZE と :ANGLE を持つことを知り、:SIZE に 50 を :ANGLE に 60 を割り当てます。次に、POLY の定義の本体を順に調べていきます。FD :SIZE という命令があります。:SIZE には 50 が割り当てられているので 50 だけ前進します。次に、RT :ANGLE という命令があります。:ANGLE には 60 が割り当てられているので、右に 60 度回転します。次は、POLY :SIZE :ANGLE という命令です。:SIZE には 50 が :ANGLE には 60 が割り当てられていますから、POLY 50 60 を実行しなければなりません。コンピュータは再び POLY の定義を調べて、上と同じことを実行します。このようなメカニズムで POLY 50 60 は 50 単位の正六角形を描き続けます。停止するには、Esc キーを押す必要があります。再帰呼び出しというのは、POLY の定義をするのに POLY を使っていることによります。頭山的ともいいます。落語の頭山からきています。数学では再帰という言葉が使われます。代表例はヒボナッチ数列の定義です。
KITE は自分自身の関数を定義することも出来ます。最大公約数を計算する関数を定義して見ましょう。TO GCD を実行して下さい。
TO GCD :A :B
IF :B == 0 [OP :A]
OP GCD :B :A % :B
END
と定義してください。有名なユークリッドの互除法のアルゴリズムです。間違いがないことを確かめたら、OK ボタンを押します。関数は単独では使えません。
PRINT GCD 24 18
を実行して下さい。
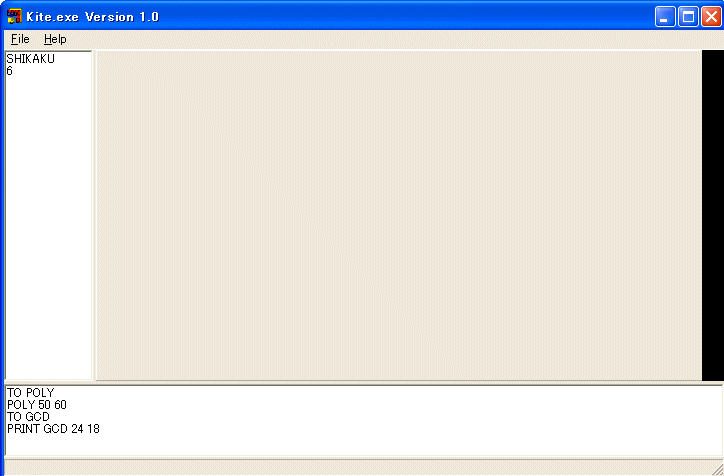
6 が左側の領域に表示されたはずです。PRINT GCD 24 18 と命令されるとコンピュータはGCD の定義を調べます。GCD は :A と :B の二つの引数を持っています。:A に 24 を :B に 18 を割り当てます。次の行は IF :B == 0 [OP :A] です。IF 文は二つの形があります。一つは IF 条件式 [ 命令の列 ] です。今の場合、条件式は :B == 0 です。:B に 0 が割り当てられていれば真、そうでなければ偽になります。条件式が真であれば [ と ] の間の命令の列を実行します。もう一つは IF 条件式 [ 命令の列 ] [ 命令の列 ] です。条件式が真であれば最初の命令の列の実行し、条件式が偽であれば二つ目の命令の列を実行します。今の場合、:B には 18 が割り当てられているので、この IF 文では何もしません。次の行は OP GCD :B :A % :B です。OP 命令は GCD :B :A % :B の値をこの関数 GCD の値として関数 GCD の実行を終了せよという命令です。即ち、GCD 24 18 の値として GCD 18 24 % 18 を返せと定義しています。% は余りを取る演算子です。24 % 18 は 24 を 18 で割った余り 6 になります。従って、GCD 18 6 を計算して、その値が GCD 24 18 であると定義しています。コンピュータは GCD 18 6 を計算するために、GCD の定義を再び調べます。今度は :A に 18 を :B に 6 を割り当てます。:B には 0 が割り当てられていませんから、今度は GCD 18 6 の値は GCD 6 0 であると指示されます。再びコンピュータは GCD の定義を調べます。今度は :A には 6 が :B には 0 が割り当てられます。二行目の IF :B == 0 [OP :A ] の条件式 :B == 0 が今度は真になります。OP :A が実行できます。:A に割り当てられている 6 を GCD 6 0 の値として関数の実行を終わります。従って、GCD 24 18 = GCD 18 6 = GCD 6 0 = 6 として、GCD 24 18 の値 6 が求まりました。PRINT GCD 24 18 は GCD 24 18 の値 6 を左の領域に表示します。
今度は最小公倍数を計算する関数を定義してみましょう。GCD 関数を使えば簡単です。TO LCM を実行します。
TO LCM :A :B
OP :A * :B / GCD :A :B
END
と定義します。* は掛け算を意味します。/ は割り算を意味します。* と / は同じ優先度ですから左から順に計算します。:A と :B を掛け、:A と :B の最大公約数で割ります。関数の定義の仕方は一通りではありません。例えば、LCM は次のように定義しても良いです。
TO LCM :A :B
LOCAL :T
:T = :A
WHILE :T % :B != 0 [:T = :T + :A ]
OP :T
END
この関数の定義の意味は次の通りです。LOCAL :T という命令は :T というローカル変数を宣言しています。変数は数値を入れる入れ物で必ず : で始まり、英字で始まる英数字の名前を持ちます。ローカル変数とは宣言された手続きや関数の定義の中だけで有効な変数です。局所変数は LOCAL 変数名の並びで宣言します。変数名の並びとは変数名の列のことです。ローカル変数の宣言は必ず一行使って宣言して下さい。次の行の :T = :A は代入文です。:T の値として :A の値を割り当てよという命令です。:T の持っていた値は捨てられます。:A に割り当てられている値に変化はありません。これを普通 :T に :A を代入するといいます。次は WHILE 文です。WHILE 条件式 [ 命令の列 ] の形で使います。条件式が真の間、命令の列を実行します。命令の列を普通、命令の並びといいます。従って、WHILE :T % :B != 0 [:T = :T + :A ] は上の行で :T に :A の値を代入しているので、:T の値が :B の値で割り切れない間は :T = :T + :A を実行します。:T = :T + :A は :T の値と :A の値の和を :T の新しい値にしなさいという代入文で :T の値が :A の値だけ増加します。従って、:A の倍数を次々 :T の値とし、:B で割り切れれば、この WHILE 文を終了します。この時、:T には :A と :B の最小公倍数が割り当てられているので、次の行で :T の値を LCNM :A :B の値としてこの関数の実行を終了すればいいのです。ついでにもう一つの定義を示します。
TO LCM :A :B
LOCAL :I :T
FOR :I = 1 TO :B [:T = :I * :A IF :T % :B == 0 [BREAK]]
OP :T
END
でも最小公倍数を計算してくれます。二行目で :I と :T の二つのローカル変数を宣言しています。三行目は FOR 文です。今回は STEP 数式の部分がありません。このような時は :I の増分は 1 です。:I を 1 から初めて :B まで [ と ] の間の命令を実行します。:T = :I * :A は代入文で :I と :A の積を :T に代入します。次の命令は IF 文です。:T % :B == 0 が条件式で :T が :B で割り切れるなら BREAK が実行されます。BREAK 命令は FOR 文や WHILE 文や REPEAT 文や DO UNTIL 文のループの実行を終了する命令です。従って、BREAK を実行すると一番内側のループを抜けます。今の場合、:A を 1 倍、2 倍、3倍としていって、:B の倍数になれば、WHILE 文の実行を終了します。この時、:T には :A と :B の最小公倍数が割り当てられているはずですから、次の行で :T をこの関数の値とします。最初のうちは、思いつく方法でプログラムを作れば良いです。最大公約数を計算する考え方の単純なプログラムとして次のような定義も出来ます。
TO GCD :A :B
LOCAL :T :I
FOR :I=1 TO :A [IF (:A % :I == 0) && (:B % :I == 0) [:T = :I]]
OP :T
END
ローカル変数 :I を 1 から :A まで変化させ、:I が :A と :B の両方を割りりるとき、即ち公約数のとき、:I の値を :T に保存しています。従って、FOR 文を終えたとき、:T には :A と :B の最大公約数がセットされています。さらに、上のプログラムではローカル変数 :T と :I を使った行儀の良いプログラムにしていますがグローバル変数を使って次のように定義しても良いです。
TO GCD :A :B
FOR :I=1 TO :A [IF (:A % :I == 0) && (:B % :I == 0) [:T = :I]]
OP :T
END
グローバル変数は宣言しなくても使えて便利ですが、深くネストした手続きで変更されたのが全体に及びますから、便利ですが、注意が必要です。下のマニュアルの LOCAL の項目を参照してください。GCD は次の様に定義すればもっと効率が良くなります。
TO GCD :A :B
LOCAL :I ;L
IF :A < :B [:L = :A][:L = :B]
FOR :I=:L DOWNTO 1 [IF (:A % :I == 0) && (:B % :I == 0) [BREAK]]
OP :I
END
:A と :B の小さいほうを :L に代入します。:I を :L から 1 まで順に小さくしていって、最初に :I が :A と :B の両方を割り切るとき :I の値が :A と :B の最大公約数ですから、BREAK 命令で FOR 文を終わります。:I を GCD :A :B の値として関数を終了します。基本的には人間が考える通りプログラムすればいいです。小学生でも実行できるぐらい細かく手順を分解できれば、大抵プログラミングできます。ただ数学と違う面もあります。例えば、:A と :B を素因数分解して、最大公約数や最小公倍数を求めるという方法は勿論可能ですがプログラム化するのは大変です。初心者の時は小さいプログラムをたくさん作ってください。実行速度が気になりだしたら、アルゴリズムの本で勉強してください。KITE では大きなプログラムは作りませんから、どんなプログラムを作ってもたいした差はないですが、KITE を卒業し、Java や C++ のコンパイラなどで、本格的なオブジェクト指向プログラミングに挑戦するようになると、アルゴリズムの勉強が重要になります。データ構造の勉強も必要です。参考書は Niklaus Wirth 著「アルゴリズム+データ構造=プログラム」日本コンピュータ協会がお勧めです。KITE にはデータ構造と呼べるものは何もありません。データは倍精度の実数だけです。本格的なプログラムでは素人の作ったプログラムとプロの作ったプログラムでは実行速度に数千倍、数万倍以上のの差が出るのは日常茶飯事です。
もとに戻って、POLY を停止するように修正しましょう。:ANGLE の値から繰り返しの回数をまず計算します。:ANGLE と 360 の最小公倍数を :ANGLE で割ったものが繰り返しの回数です。
TO POLY :SIZE :ANGLE
LOCAL :T
:T = (LCM :ANGLE 360) / :ANGLE
REPEAT :T [FD :SIZE RT :ANGLE]
END
この様に POLY を定義すれば、例えば POLY 100 144 と実行すれば、星型正五角形を描いて停止するはずです。
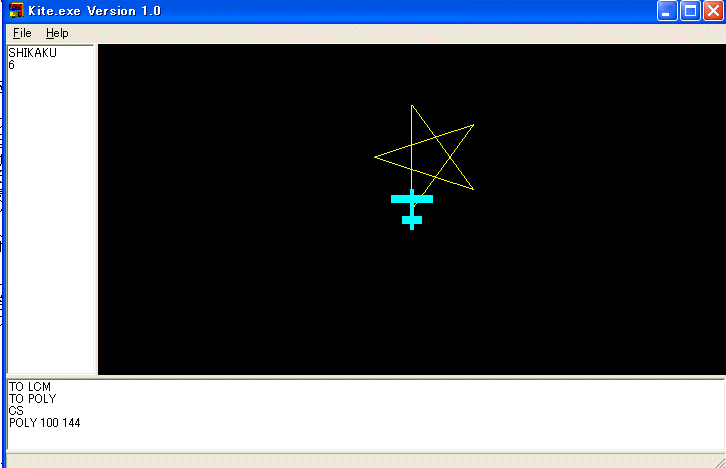
次の様に定義しても良いです。回転角の合計を保存していて、360 の倍数になれば停止します。
TO POLY :SIZE :ANGLE
LOCAL :T
:T = 0
DO [
FD :SIZE RT :ANGLE
:T := :T + :ANGLE
] UNTIL :T % 360 == 0
END
DO UNTIL 文は DO [ 命令の列 ] UNTIL 条件式 の形をしていて、まず命令の列を実行し、条件式を調べます。条件式が偽の間は命令の列を繰り返し実行します。WHILE 文は条件が偽であれば一回も命令の列を実行しませんが、DO UNTIL 文は条件が真でも一回は命令の列を実行します。引数を増やして、回転角の合計を再帰呼び出しの引数として渡すことも出来ます。
TO POLY :SIZE :ANGLE :JUNK
FD :SIZE RT :ANGLE
:JUNK = :JUNK + :ANGLE
IF :JUNK % 360 == 0 [STOP]
POLY :SIZE :ANGLE :JUNK
END
でもいいはずです。POLY 100 144 0 のように使います。
Harold Abelson and Andrea diSessa : TURTLE GEOMETRY (The Computer as a Medium for Exploring Mathmatics), The MIT Press には生物の動きのシミュレーションのプログラムなどおもしろいものがたくさん載っています。この本を参考して、次に生物の動きをシミュレートしてみましょう。
TO ANIMAL
CS PU LT 90 FD 200 RT 90 PD
ST2
SUBANIMAL
END
TO SUBANIMAL
FD 5 RT 10 TOWARD2 FD2 5
IF DISTANCE2 < 5 [STOP]
SUBANIMAL
END
と定義します。TO ANIMAL を実行して、ANIMAL の定義だけでなく、SUBANIMAL の定義も続けて定義することが出来ます。
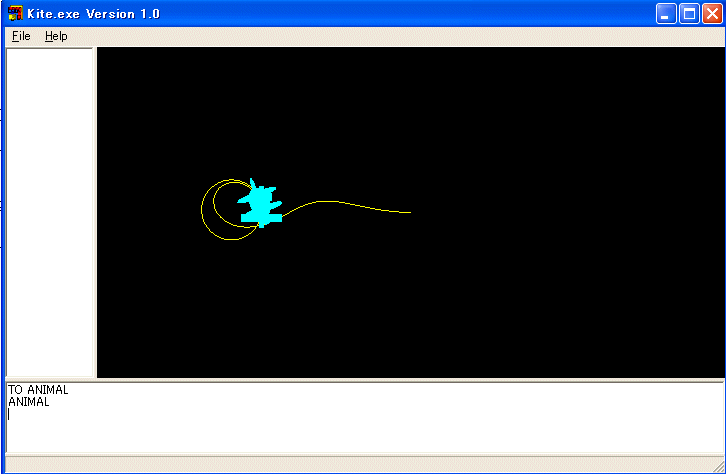
ANIMAL は CS で画面を初期化し、PU LT 90 FD 200 RT 90 PD で一匹目のタートルを XY 平面の (-200, 0) の位置に移します。次に ST2 で二匹目のタートルを表示します。最後に、 SUBANIMAL を呼び出します。SUBANIMAL は一匹目のタートルが五歩前進し、右に10度向きを変えます。次に二匹目のタートルが一匹目のタートルの方向に向きを変え、五歩前進します。次の IF DISTANCE2 < 5 [STOP] でもし二つのタートルの距離が五歩分より短ければ、STOP を実行します。STOP 文はこれで SUBANIMAL の実行を終了せよという命令です。二つのタートルの距離が五歩分より短かくなければ、次の行に制御が移ります。SUBANIMAL を実行します。再帰呼び出しです。従って、SUBANIMAL は一匹目のタートルが円運動をしている時、二匹目のタートルが一匹目のタートルを見ながら追いかける時の軌跡を描く手続きです。
別の例を考えます。四匹のタートルの動きをシミュレートします。実際のタートルは二匹しかいませんから技巧が必要です。TO ANIMAL4 をコマンドラインから実行し、ダイアログボックスのメモに次のように打ち込んで下さい。
TO ANIMAL4
CS PU
SETPOS -150 (-150) 0 PUT 1 0
SETPOS -150 150 0 PUT 1 1
SETPOS 150 150 0 PUT 1 2
SETPOS 150 (-150) 0 PUT 1 3
SUBANIMAL4 0
END
TO SUBANIMAL4 :I
IF :I == 0 [
GET 1 1 PU2 GET 2 0 TOWARD2 PD2 FD2 5 PUT 2 4
GET 1 2 PU2 GET 2 1 TOWARD2 PD2 FD2 5 PUT 2 5
GET 1 3 PU2 GET 2 2 TOWARD2 PD2 FD2 5 PUT 2 6
GET 1 0 PU2 GET 2 3 TOWARD2 PD2 FD2 5 PUT 2 7
IF DISTANCE2 < 5 [STOP]
SUBANIMAL4 1
][
GET 1 5 PU2 GET 2 4 TOWARD2 PD2 FD2 5 PUT 2 0
GET 1 6 PU2 GET 2 5 TOWARD2 PD2 FD2 5 PUT 2 1
GET 1 7 PU2 GET 2 6 TOWARD2 PD2 FD2 5 PUT 2 2
GET 1 4 PU2 GET 2 7 TOWARD2 PD2 FD2 5 PUT 2 3
IF DISTANCE2 < 5 [STOP]
SUBANIMAL4 0
]
END
と定義します。
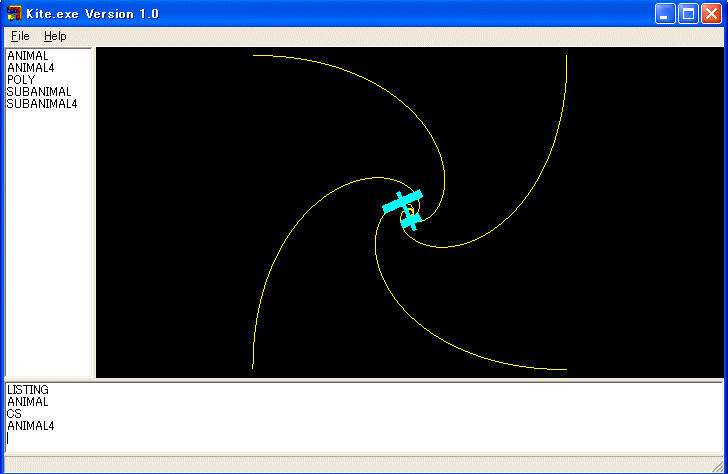
KITE にはタートルの状態を保存する配列が備わっています。配列に保存するのに PUT 数式1 数式2 の形で命令します。現在の数式1 番目のタートルの状態を配列の数式2 番目の位置に保存します。GET 数式1 式2 の形で数式1 番目のタートルの状態を配列の数式2 番目の位置に保存されているタートルの状態に変更します。配列の大きさは100個ぶんです。0 から 99 までの位置が使えます。また、タートルを移動するのに SETPOS 数式1 数式2 数式3 の形の命令を使うことも出来ます。座標 (数式1, 数式2, 数式3) を持つ位置にタートルが移動します。他のタートルの状態は変化しません。従って、ANIMAL4 の命令は画面を初期化し、ペンを上げ、タートルを順に(-150, -150, 0), (-150, 150, 0), (150, 150, 0), (150, -150, 0) に移動し、配列の 0, 1, 2, 3 番目の位置にその状態を保存しています。-150 が ( ) で囲まれていることに注意してください。括弧がなく SETPOS 150 -150 0 では、SETPOS に三個の引数が与えられているとは解釈されず 150-150 即ち 0 と 0 の二つの引数しか与えられていないと解釈されますのでくれぐれも間違えないようにして下さい。そして、SUBANIMAL4 0 を呼び出しています。SUBANIMAL4 は引数を一つ持ちます。引数には 0 か 1 が与えられます。0 が与えられた時は、一匹目のタートルに配列の 1 番目の状態をセットし、二番目のタートルのペンを上げ、配列の 0 番目の状態をセットし、一匹目のタートルの方を向き、五歩前進します。そしてその状態を配列の 4 番目の位置に保存します。この様な操作を四つの位置について実行します。そして、二匹のタートルの距離が五歩より近くなれば実行を停止します。そうでなければ、SUBANIMAL4 1 を実行します。引数が 1 の時の SUBANIMAL4 も同様に動作します。ぜひ、プログラムを打ち込んで実行してみて下さい。
KITE は三次元 LOGO です。タートルは三次元空間を動くことが出来ます。左右に向きを変えるだけでなく、上下に向きを変えたり、右肩下がりや左肩下がりに状態を変化することが出来ます。これらの命令は下の手続きのマニュアルを読んでください。これにより前進だけで自由に空間を移動できます。例えば、
REPEAT 360 [FD 10 RT 10 UP 20]
を実行すれば、常螺旋を描きます。
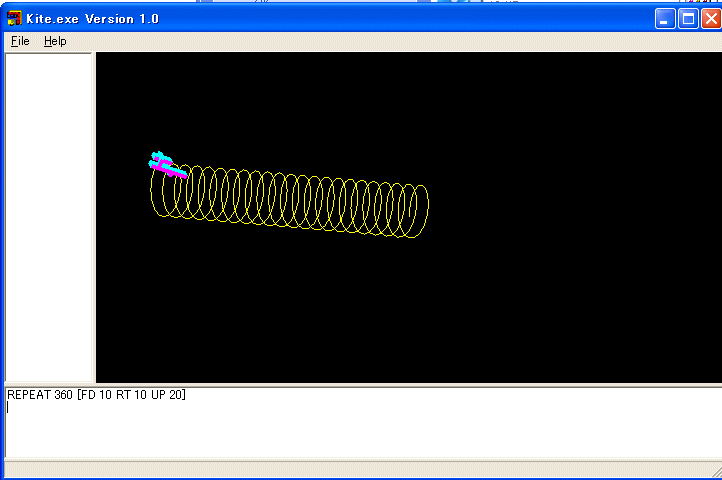
常螺旋であることを実感したければ、マウスで画面をドラッグしてみて下さい。
そもそも KITE を作ろうと思った動機は MICRO LOGO で小学校の教員希望の学生たちの教育をしている時、立方体をどのように描けばいいか質問を受けたことです。平面 LOGO で正確な立方体の色々な投影図を描くのは難しいので、コンピュータで簡単に描けるように空間 LOGO を作りました。立方体を描くには次のようにします。
TO cube :x
repeat 4 [fd :x down 90 fd :x bk :x up 90 rt 90]
down 90 fd :x up 90
repeat 4 [fd :x rt 90]
down 90 bk :x up 90
end
と定義すれば、cube 100 のように使う立方体を描く手続きを定義できます。
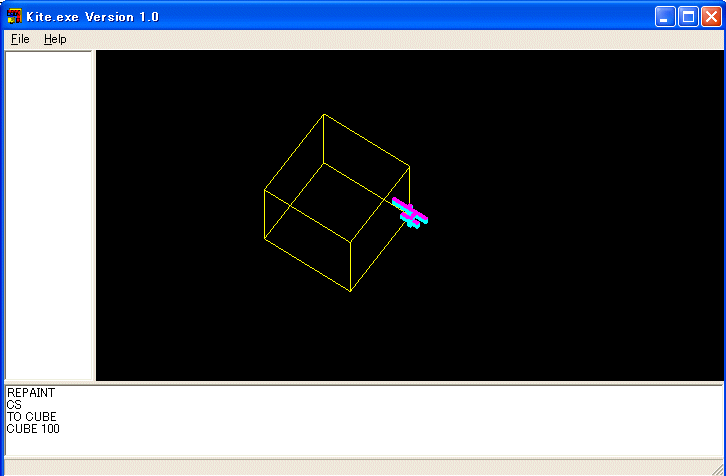
この図は立方体を描いたことが分かるようにマウスで回転しています。down 90 は頭を 90 度下げよという命令で、up 90 は頭を 90 度上げよという命令です。立方体は分かりやすいですね。直方体を描く手続きを作ってみましょう。
立方体や直方体は小学生での理解できると思いますが、その他の図形はとたんに難しくなります。タートルグラフィックスに拘ると、正四面体を描くためには、解析幾何学でもだめで、球面幾何学の知識が必要になります。解析幾何学を使って三次元の図形を描くソフトはフリーソフトの POV-Ray があるので、タートルグラフィックスに拘ります。
TO TETRA :S
REPEAT 3 [FD :S RT 120]
YAW 180 - ACOS 1/3
REPEAT 3 [FD :S LT 120]
LT 60 YAW 180 - ACOS 1/3
REPEAT 3 [FD :S LT 120]
YAW -180 + ACOS 1/3 RT 60 YAW -180 + ACOS 1/3
END
と定義すれば、TETRA 100 のように使う正四面体を描く手続きを定義できます。
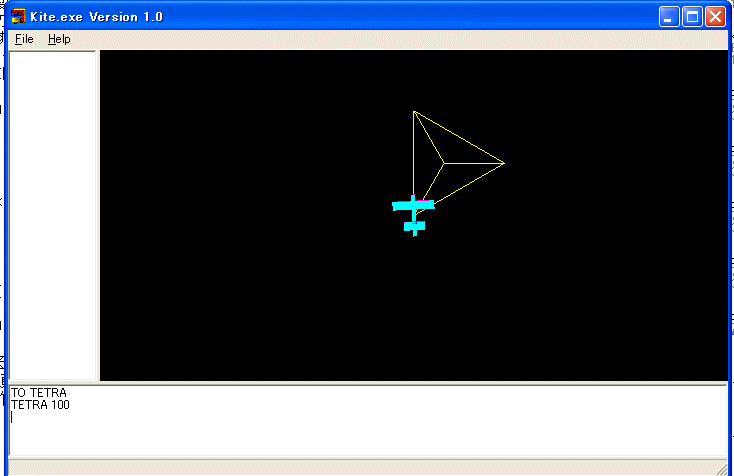
球面幾何学で習う余弦法則を使えば良いです。三角形 ABC は球面三角形で、辺 a は頂点 A に、辺 b は頂点 B に、辺 c は頂点 C に対するものとする。辺の余弦法則:cos a = cos b cos c + sin b sin b cos A と角の余弦法則:cos A = - cos B cos C + sin B sin C cos a というやつです。辺の余弦法則を使って、正四面体の面の間の角が arccos 1/3 であることが分かります。YAW 数値 が体を傾ける命令です。他の正多面体を描くにはどのように定義すればいいのでしょうか?考えてみて下さい。結構面倒くさいです。挑戦してみてください。サンプルプログラムに一つの解答を与えています。KITE は座標を使って三次元の図形を描く機能もサポートしましたが、KITE ではそのようにして描いた図形は柔軟性がありませんから(回転したり平行移動したりして、他のプログラムの部品として使うことがタートルグラフィックスのように自由にはならない)ので、タートルグラフィックスに拘っています。それで、三次元の機能の大部分は大学生しか使いこなせないものになってしまいました。
Synchro という命令を導入しました。Synchro 命令を実行した時には、シンクロ状態になり、二匹目のタートルが移動した時、両方のタートルが PD ならば二匹のタートル間に線が引かれます。NonSynchro 命令を実行すれば、シンクロ状態を抜けます。初期状態はシンクロ状態ではありません。例えば次のように使います。
CS PU FD 100 PD UP 90 ST2 UP2 90
SYNCHRO
REPEAT 36 [FD 10 RT 10 FD2 10 RT2 10]
NONSYNCHRO
で円柱を描きます。

円柱に見えませんね。カメラを移動してみましょう。
FOR :I=0 TO 360 [LOOKAT 500*COS :I 500*SIN :I 500 0 0 0 0 1 0]
面白いでしょう。絵ではお見せできませんから、是非実行してみて下さい。LOOKAT 命令はマニュアルの手続きの解説を読んでください。双曲放物面はねじれ四角形の一組の対辺の等分点同士を結ぶことで描くことが出来ます。マックレアによる模型を作る方法も知られています。「不思議おもしろ幾何学事典 朝倉書店」をお読み下さい。
主な使い方は紹介しましたが、まだまだたくさんの機能があります。マニュアルやサンプルプログラムを読んで面白い図を描いてください。面白いプログラムが出来たら、作者にも教えてください。osamu@cc.kochi-u.ac.jp までメールをいただければ幸いです。バグ情報やこんな機能があれば非常に便利だというものを思いつかれたら(例えば線だけでなく、面も描けるようにするのは、タートルグラフィックスと整合性を取るのが難しいなどのように、答えられるかどうか分かりませんが)同様に教えてください。では、三次元 LOGO の世界をお楽しみください。LOGO の本格的な参考書は TURTLE GEOMETRY がお勧めです。






























