三次元双曲空間の例として、正多面体を描いてみます。以下のプログラムはユークリッド空間でも(KITE でも)通用するプログラムです。
まず正四面体です。
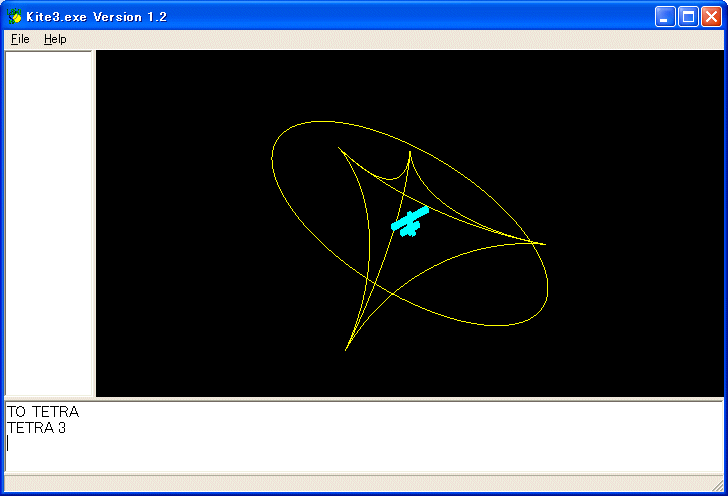
プログラムは以下のようなものです。TETRA 3 を実行しています。
TO TETRA :A
LOCAL :THETA
:THETA = ACOS -1/3
PU FD :A PUT 1 0 BK :A
DOWN :THETA
FD :A PUT 1 1 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 2 BK :A
UP :THETA-90 RT 120 DOWN :THETA-90
FD :A PUT 1 3 BK :A
UP :THETA
PUSH PUSH2
GET 1 0 PD PU2 GET 2 1 PD2
SYNCHRO
GET 2 2 GET 2 3 GET 2 1
NONSYNCHRO
GET 2 2 GET 2 3 GET 2 1
PU POP PD PU2 POP2 PD2
END
次は立方体です。
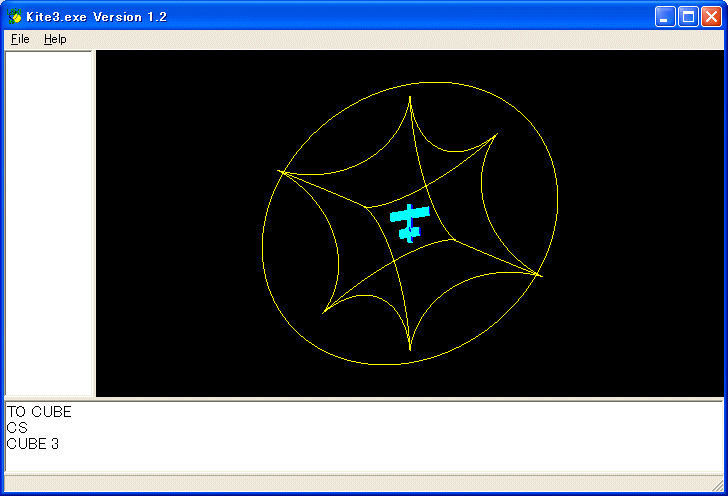
プログラムは以下のようなものです。CUBE 3 を実行しています。
TO CUBE :A
LOCAL :THETA
:THETA = ACOS 1/3
PU
FD :A PUT 1 0 BK 2*:A PUT 1 6 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 5 FD :A
DOWN 90-:THETA RT 120 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 2 FD :A
DOWN 90-:THETA RT 120 UP 90
PUSH PUSH2
PU GET 1 0 PD
GET 1 3 GET 1 2 GET 1 1 GET 1 0
GET 1 1 GET 1 5 GET 1 4 GET 1 0
GET 1 4 GET 1 7 GET 1 3 GET 1 0
PU GET 1 6 PD
GET 1 5 GET 1 1 GET 1 2 GET 1 6
GET 1 2 GET 1 3 GET 1 7 GET 1 6
GET 1 7 GET 1 4 GET 1 5 GET 1 6
PU POP PD PU2 POP2 PD2
END
次は正八面体です。
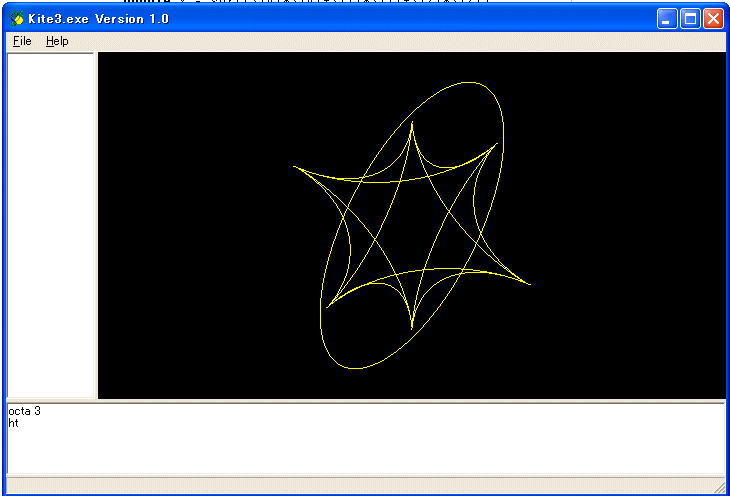
プログラムは以下のようなものです。OCTA 3 を実行しています。 引数は対角線の長さの半分です。
TO octa :a
push push2
pu
for :i=0 to 3 [fd :a put 1 :i bk :a rt 90]
up 90 fd :a put 1 4 bk :a
up 180 fd :a put 1 5
get 1 4 pd pu2 get 2 0 pd2
synchro
get 2 1 get 2 2 get 2 3 get 2 0
nonsynchro
get 2 1 get 2 2 get 2 3 get 2 0
pu get 1 5 pd
synchro
get 2 1 get 2 2 get 2 3 get 2 0
nonsynchro
pu pop pd pu2 pop2 pd2
end
次は正十二面体です。
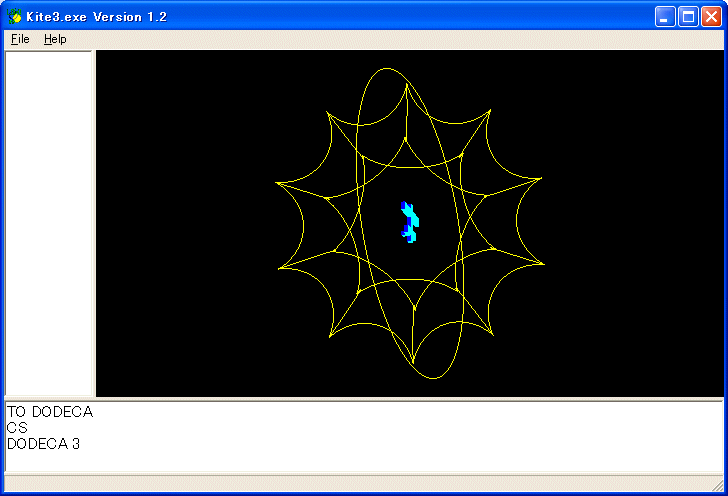
プログラムは以下のようなものです。DODECA 3 を実行しています。
TO DODECA :A
LOCAL :PHI :THETA
:PHI=ACOS (COT 36)*(COT 60)
:THETA=2*ACOS (COS 36)/(SIN 60)
PU
DOWN :PHI
FD :A PUT 1 0 BK 2*:A PUT 1 18 FD :A
DOWN :THETA
FD :A PUT 1 5 BK 2*:A PUT 1 12 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 1 BK 2*:A PUT 1 19 FD :A
DOWN :THETA
FD :A PUT 1 6 BK 2*:A PUT 1 13 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 2 BK 2*:A PUT 1 15 FD :A
DOWN :THETA
FD :A PUT 1 7 BK 2*:A PUT 1 14 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 3 BK 2*:A PUT 1 16 FD :A
DOWN :THETA
FD :A PUT 1 8 BK 2*:A PUT 1 10 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90-:PHI
FD :A PUT 1 4 BK 2*:A PUT 1 17 FD :A
DOWN :THETA
FD :A PUT 1 9 BK 2*:A PUT 1 11 FD :A
DOWN 90-:PHI-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD
GET 1 1 GET 1 2 GET 1 3 GET 1 4 GET 1 0
GET 1 5 GET 1 10 GET 1 6 GET 1 1 GET 1 0
PU GET 1 1 PD
GET 1 6 GET 1 11 GET 1 7 GET 1 2 GET 1 1
PU GET 1 2 PD
GET 1 7 GET 1 12 GET 1 8 GET 1 3 GET 1 2
PU GET 1 3 PD
GET 1 8 GET 1 13 GET 1 9 GET 1 4 GET 1 3
PU GET 1 4 PD
GET 1 9 GET 1 14 GET 1 5 GET 1 0 GET 1 4
PU GET 1 5 PD
GET 1 14 GET 1 15 GET 1 16 GET 1 10 GET 1 5
PU GET 1 6 PD
GET 1 10 GET 1 16 GET 1 17 GET 1 11 GET 1 6
PU GET 1 7 PD
GET 1 11 GET 1 17 GET 1 18 GET 1 12 GET 1 7
PU GET 1 8 PD
GET 1 12 GET 1 18 GET 1 19 GET 1 13 GET 1 8
PU GET 1 9 PD
GET 1 13 GET 1 19 GET 1 15 GET 1 14 GET 1 9
PU GET 1 15 PD
GET 1 19 GET 1 18 GET 1 17 GET 1 16 GET 1 15
PU POP PD PU2 POP2 PD2
END
正多面体の最後は正二十面体です。
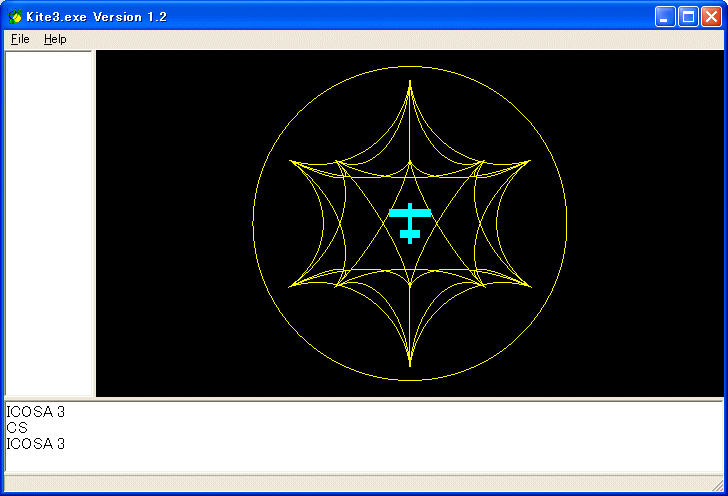
TO ICOSA :A
LOCAL :THETA
:THETA = 2*ACOS (COS 60)/(SIN 36)
PU
FD :A PUT 1 0 BK 2*:A PUT 1 11 FD :A
DOWN :THETA
FD :A PUT 1 1 BK 2*:A PUT 1 8 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 2 BK 2*:A PUT 1 9 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 3 BK 2*:A PUT 1 10 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 4 BK 2*:A PUT 1 6 FD :A
DOWN 90-:THETA LT 72 UP 90-:THETA
FD :A PUT 1 5 BK 2*:A PUT 1 7 FD :A
DOWN 90-:THETA LT 72 UP 90
PUSH PUSH2
PU GET 1 0 PD PU2 GET 2 1 PD2
SYNCHRO
GET 2 5 GET 2 4 GET 2 3 GET 2 2 GET 2 1
NONSYNCHRO
GET 2 5 GET 2 4 GET 2 3 GET 2 2 GET 2 1
PU GET 1 6 PD
SYNCHRO
GET 2 2 GET 1 7 GET 2 2 GET 2 3 GET 1 8 GET 2 3 GET 2 4
GET 1 9 GET 2 4 GET 2 5 GET 1 10 GET 2 5 GET 2 1 GET 1 6 GET 2 1
NONSYNCHRO
PU GET 1 11 PD PU2 GET 2 6 PD2
SYNCHRO
GET 2 10 GET 2 9 GET 2 8 GET 2 7 GET 2 6
NONSYNCHRO
GET 2 10 GET 2 9 GET 2 8 GET 2 7 GET 2 6
PU POP PD PU2 POP2 PD2
END
平面双曲幾何の例を挙げます。 双曲幾何の三角形に関する公式が必要です。
△ABC は双曲三角形で、三辺の長さが a, b, c で、対応する内角が A, B, C の時、
正弦法則は
sinh a / sin A = sinh b / sin B = sinh c / sin C
で、余弦法則は
cosh a = cosh b cosh c - sinh b sinh c cos A
cosh b = cosh c cosh a - sinh c sinh a cos B
cosh c = cosh a cosh b - sinh a sinh b cos C
です。
さらに、第二余弦法則
cosh a = (cos B cos C + cos A) / (sin B sin C)
cosh b = (cos C cos A + cos B) / (sin C sin A)
cosh c = (cos A cos B + cos C) / (sin A sin B)
が成り立ちます。証明は「ユークリッド幾何から現代幾何へ」小林昭七著 日本評論社がわかりやすい参考書です。
三つの角度が与えられたとき、その角度を持つ三角形を描くプログラムです。申すまでもないことですが、三角形の内角の和は180度より小さいことに注意して下さい。辺の長さは角度より自動的に定まります。 第二余弦定理を使っています。
TO tri :alpha :beta :gamma
local :a :b :c
:a = acosh ((cos :beta)*(cos :gamma)+(cos :alpha))/((sin :beta)*(sin :gamma))
:b = acosh ((cos :alpha)*(cos :gamma)+(cos :beta))/((sin :alpha)*(sin :gamma))
:c = acosh ((cos :alpha)*(cos :beta)+(cos :gamma))/((sin :alpha)*(sin :beta))
fd :a rt 180-:beta fd :c rt 180-:alpha fd :b rt 180-:gamma
end
REPEAT 12 [TRI 30 30 30 RT 30] を実行すると次のようになります。
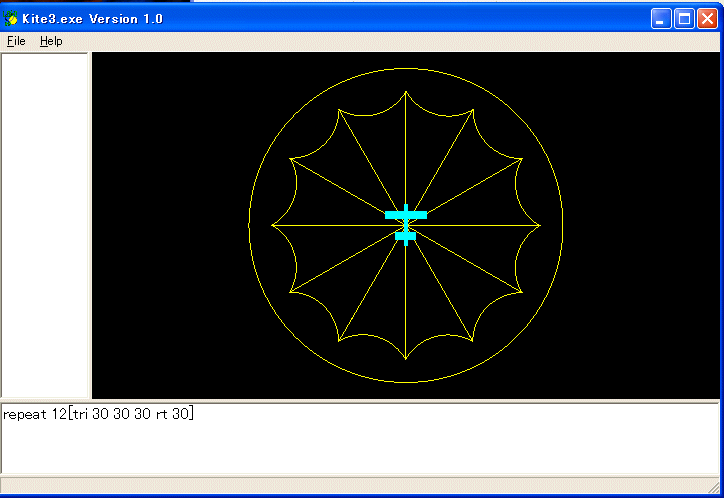
余弦定理を使うと三つの辺の長さが与えられた三角形を描くプログラムを作れます。
三つの辺は三角不等式(:a+:b<:c, :b+:c<:a および :c+:a<:b)を満たしている必要があります。
TO tri :a :b :c
local :alpha :beta :gamma
:alpha = acos ((cosh :b)*(cosh :c)-(cosh :a))/((sinh :b)*(sinh :c))
:beta = acos ((cosh :a)*(cosh :c)-(cosh :b))/((sinh :a)*(sinh :c))
:gamma = acos ((cosh :a)*(cosh :b)-(cosh :c))/((sinh :a)*(sinh :b))
fd :a rt 180-:beta fd :c rt 180-:alpha fd :b rt 180-:gamma
end
です。これをちょっと変えて、次のようにします。 TRI 1 1 1 3 を実行します。
TO tri :a :b :c :n
local :alpha :beta :gamma
:alpha = acos ((cosh :b)*(cosh :c)-(cosh :a))/((sinh :b)*(sinh :c))
:beta = acos ((cosh :a)*(cosh :c)-(cosh :b))/((sinh :a)*(sinh :c))
:gamma = acos ((cosh :a)*(cosh :b)-(cosh :c))/((sinh :a)*(sinh :b))
if :n ==0[stop]
fd :a tri :a :b :c :n-1 rt 180-:beta
fd :c tri :a :b :c :n-1 rt 180-:alpha
fd :b tri :a :b :c :n-1 rt 180-:gamma
end
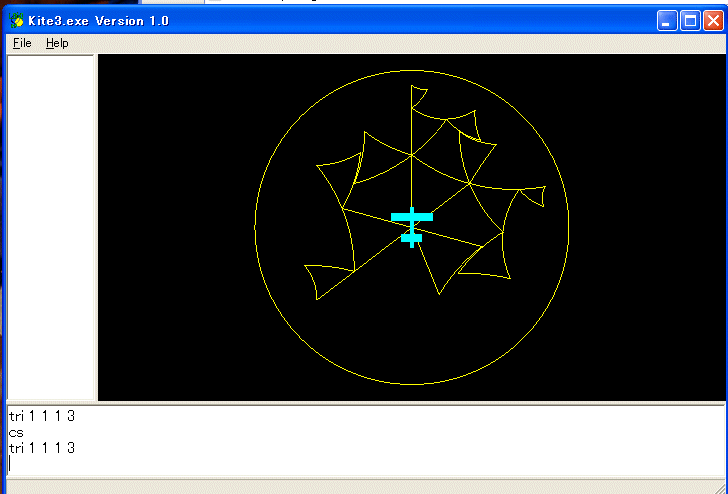
次は TILING の例です。
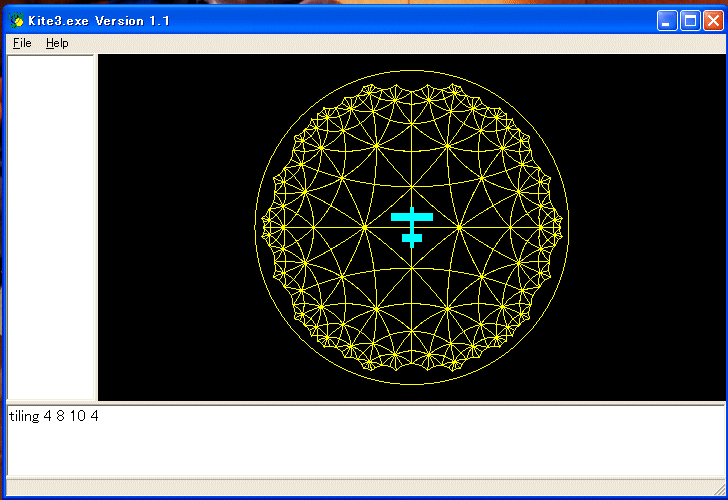
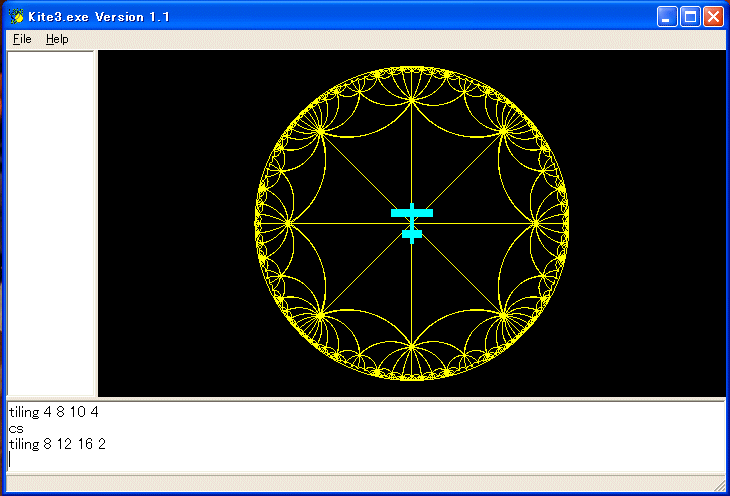
プログラムは以下のようなものです。 :n1, :n2, :n3 は 1/:n1+1/:n2+1/:n3 < 1/2 を満たす偶数です。グラフの横優先探索のテクニックを使っています。
TO tiling :n1 :n2 :n3 :n
local :alpha :beta :gamma :a :b :c :i :k :sind :tind :ind :flag
:alpha = 360/:n1
:beta = 360/:n2
:gamma = 360/:n3
:a = acosh ((cos :beta)*(cos :gamma)+(cos :alpha))/((sin :beta)*(sin :gamma))
:b = acosh ((cos :alpha)*(cos :gamma)+(cos :beta))/((sin :alpha)*(sin :gamma))
:c = acosh ((cos :alpha)*(cos :beta)+(cos :gamma))/((sin :alpha)*(sin :beta))
:len = 0
push
for :i=0 to :n1-1 [
if :i % 2 == 0 [
fd :c rt 180-:beta
put 1 :len pa :len*2 1 pa :len*2+1 0 :len=:len+1
fd :a rt 180-:gamma
fd :b rt 180-:alpha
][
fd :b rt 180-:gamma
put 1 :len pa :len*2 2 pa :len*2+1 1 :len=:len+1
fd :a rt 180-:beta
fd :c rt 180-:alpha
]
rt :alpha
]
:sind=0
:tind=:len
for :k=1 to :n [
while :sind <= :tind-1 [
pu get 1 :sind pd
:ind = ga :sind*2
:flag = ga :sind*2+1
if :ind==0 [
for :i=0 to :n1-1 [
if :i % 2 == :flag [
fd :c rt 180-:beta
if contained 0 :len [][
put 1 :len pa :len*2 1 pa :len*2+1 0 :len=:len+1
]
fd :a rt 180-:gamma
if contained 0 :len [][
put 1 :len pa :len*2 2 pa :len*2+1 0 :len=:len+1
]
fd :b rt 180-:alpha
][
fd :b rt 180-:gamma
if contained 0 :len [][
put 1 :len pa :len*2 2 pa :len*2+1 1 :len=:len+1
]
fd :a rt 180-:beta
if contained 0 :len [][
put 1 :len pa :len*2 1 pa :len*2+1 1 :len=:len+1
]
fd :c rt 180-:alpha
]
rt :alpha
]
]
if :ind==1 [
for :i=0 to :n2-1 [
if :i % 2 == :flag [
fd :a rt 180-:gamma
if contained 0 :len [][
put 1 :len pa :len*2 2 pa :len*2+1 0 :len=:len+1
]
fd :b rt 180-:alpha
if contained 0 :len [][
put 1 :len pa :len*2 0 pa :len*2+1 0 :len=:len+1
]
fd :c rt 180-:beta
][
fd :c rt 180-:alpha
if contained 0 :len [][
put 1 :len pa :len*2 0 pa :len*2+1 1 :len=:len+1
]
fd :b rt 180-:gamma
if contained 0 :len [][
put 1 :len pa :len*2 2 pa :len*2+1 1 :len=:len+1
]
fd :a rt 180-:beta
]
rt :beta
]
]
if :ind==2 [
for :i=0 to :n3-1 [
if :i % 2 == :flag [
fd :b rt 180-:alpha
if contained 0 :len [][
put 1 :len pa :len*2 0 pa :len*2+1 0 :len=:len+1
]
fd :c rt 180-:beta
if contained 0 :len [][
put 1 :len pa :len*2 1 pa :len*2+1 0 :len=:len+1
]
fd :a rt 180-:gamma
][
fd :a rt 180-:beta
if contained 0 :len [][
put 1 :len pa :len*2 1 pa :len*2+1 1 :len=:len+1
]
fd :c rt 180-:alpha
if contained 0 :len [][
put 1 :len pa :len*2 0 pa :len*2+1 1 :len=:len+1
]
fd :b rt 180-:gamma
]
rt :gamma
]
]
:sind=:sind+1
]
:sind=:tind :tind=:len
]
pu pop pd
end
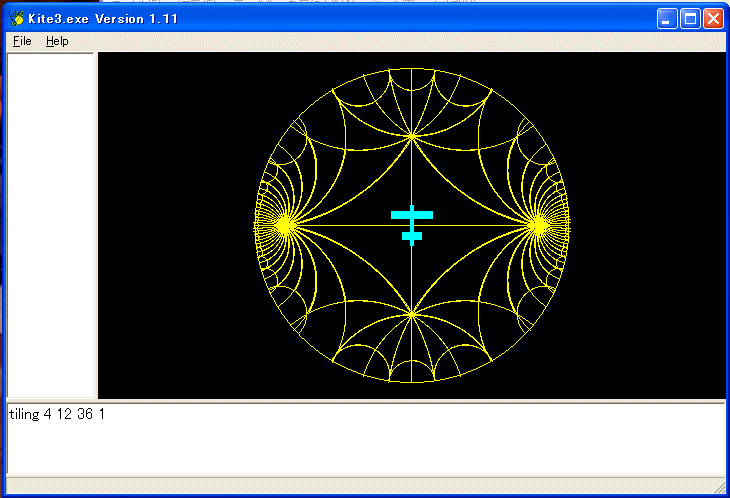
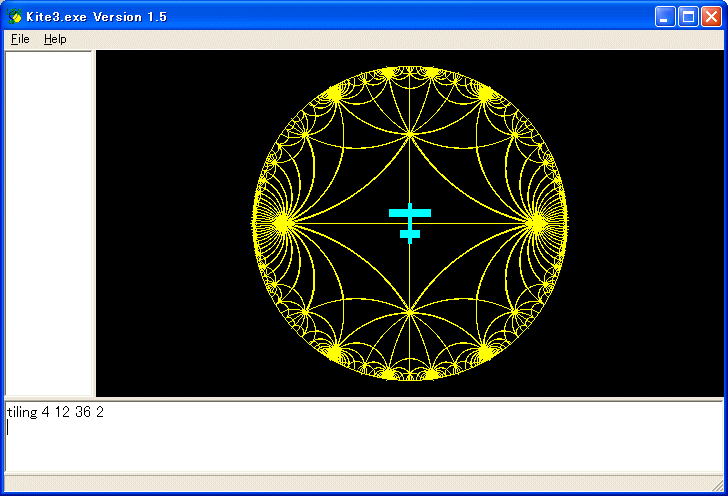
これらを描くためには、上のプログラムの10行目の push を push pu に変え、すべての fd :c rt 180-:beta のような命令の上下に :ox = tx :oy=ty :oz=tz と fullline :ox :oy :oz tx ty tz を入れて、
:ox = tx :oy=ty :oz=tz
fd :c rt 180-:beta
fullline :ox :oy :oz tx ty tz
のように変えて下さい。
次は正多角形のタイル貼りの例です。
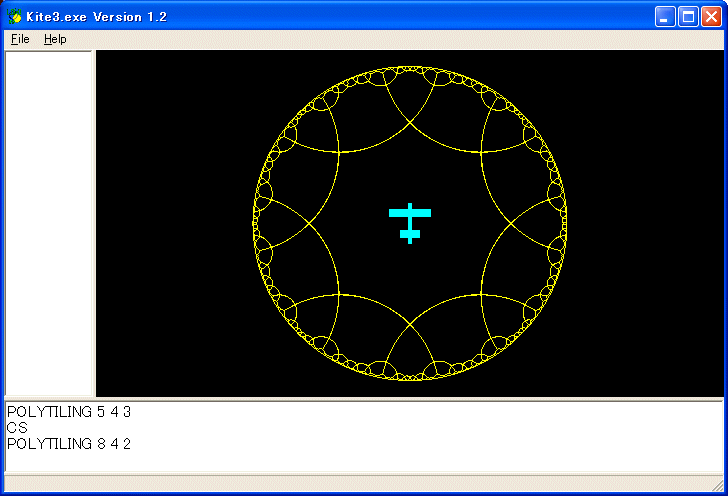
プログラムは以下のようなものです。 :N は正 :N 角形を描くことを、:M は各頂点のまわりに正 :N 角形が :L 個あることを、:L はレベルを指定します。上図は POLYTILING 8 4 2 を実行しています。三角形のタイル貼りに比べるとプログラムが簡単です。
TO POLYTILING :N :M :L
LOCAL :ANGLE :R :S :LEN :SIND :TIND
IF 2/:M >= (:N-2)/:N [STOP]
:ANGLE = 360 / :M
:S = ACOSH ((COS :ANGLE/2)*(COS :ANGLE/2)+(COS 360/:N))/
((SIN :ANGLE/2)*(SIN :ANGLE/2))
:R = ACOSH ((COS :ANGLE/2)*(COS 360/:N)+(COS :ANGLE/2))/
((SIN :ANGLE/2)*(SIN 360/:N))
PUSH PU FD :R RT 180 - :ANGLE/2 PD
:ANGLE = 180 - :ANGLE
:LEN = 0
REPEAT :N [FD :S RT :ANGLE PUT 1 :LEN :LEN = :LEN+1]
:SIND = 0
:TIND = :LEN
FOR :K=1 TO :L [
WHILE :SIND <= :TIND-1 [
PU GET 1 :SIND PD
REPEAT :M [
REPEAT :N [
FD :S RT :ANGLE
IF CONTAINED 0 :LEN [][
PUT 1 :LEN :LEN = :LEN+1
]
]
RT 180-:ANGLE
]
:SIND = :SIND+1
]
:SIND = :TIND
:TIND = :LEN
]
PU POP PD
END
では、双曲幾何学の TURTLE GEOMETRY の世界をお楽しみ下さい。












